|
(B.1) |
'Lewis-style' axiomatizations of S1°-S5:
S1°-S1; S2°-T;
S3°-S3; S4°-S5 |
| |
These axiomatizations have K, N, and M primitive (L
defined as NMN and  ab
as NMKaNb).
Rules of inference are substitution for variables, strict detachment,
adjunction, and substitutivity of strict equivalence. ab
as NMKaNb).
Rules of inference are substitution for variables, strict detachment,
adjunction, and substitutivity of strict equivalence. |
| |
Axioms for
S1°: |
| |
| M1: |
|
 KpqKqp KpqKqp |
| M2: |
|
 Kpqp Kpqp |
| M3: |
|
 KKpqrKpKqr KKpqrKpKqr |
| M4: |
|
 pKpp pKpp |
| M5: |
|
 K K pq pq qr qr pr pr |
|
| |
Axioms for S2°: |
| |
M1-M5 plus |
| |
| M7: |
|
 MKpqMp MKpqMp |
|
| |
Axioms for S3°: |
| |
M1-M5 plus |
| |
|
| |
Axioms for S4°: |
| |
M1-M5 plus |
| |
| M9: |
|
 MMpMp MMpMp |
|
| |
Axioms for T°: |
| |
Where a
is any PC thesis, add LLa
to S1° |
| |
Axioms for Sl, S2, S3,
S4, T: |
| |
Add |
| |
| M6: |
|
 pMp pMp |
|
| |
to the respective 'nought
system'. |
| |
Axioms
for S5: |
| |
M1-M5 plus |
| |
| M10: |
|
 MpLMp MpLMp |
|
| |
|
|
(B.2) |
'Lemmon-style'
bases for S1°-S5;
S1°-T;
S3°-S5 |
| |
These axiomatizations have C, N, and L primitive (M
defined as NLN and  as
LC). They are all based on classical PC; axioms for PC
may be taken as CN1, CN2, and CN3, with
substitution for variables and material detachment. In addition to PC,
the bases are as follows: as
LC). They are all based on classical PC; axioms for PC
may be taken as CN1, CN2, and CN3, with
substitution for variables and material detachment. In addition to PC,
the bases are as follows: |
| |
Basis for Sl°: |
| |
Axiom: |
| |
|
| |
Rules of Inference: |
| |
| RL1: |
|
|
| BKW: |
|
If both
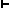
 ab
and ab
and 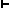
 ba,
then ba,
then 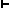
 LaLb. LaLb. |
| RLE: |
|
If
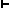 La,
then La,
then 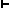 a.
a. |
| |
|
|
|
| |
Basis for S2°: |
| |
Axiom: |
| |
|
| |
Rules of Inference: |
| |
| RLE: |
|
If
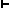 La,
then La,
then 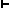 a (same
as Sl°)
a (same
as Sl°) |
| RL2: |
|
If
a
is a PC theorem or a theorem of form CLbg, then
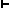 La La |
| |
|
|
|
| |
Basis for T°: |
| |
Same as for S2°, except replace RL2 by: |
| |
| RL: |
|
If
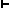 a,
then a,
then 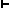 La La |
| |
|
|
|
| |
Basis for S3°: |
| |
Axiom: |
| |
|
| |
Rules of Inference: |
| |
RLE and RL2 as for S2° |
| |
|
| |
Basis for
S4°: |
| |
Same as for S3°, except replace RL2 with
RL as in T°. |
| |
|
| |
Bases for S1, S2,
S3,
S4: |
| |
Replace rule RLE in the respective 'nought' system with
axiom |
| |
|
| |
In addition, for
S1 only, add the following clause to RL1 |
| |
| |
|
. . ., or |
| (c) |
|
a is
of form CLbb |
|
| |
For S3 and S4, axiom L4 may be replaced by
axiom |
| |
|
| |
|
| |
Basis for S5: |
| |
Add to T (or to any of the systems of this section
(B.2)) axiom |
| |
|
| |
|
|
(B.3) |
Systems between S4 and S5, and
Sobocinski's 'non-Lewis modal' systems |
| |
These systems may be considered to be based on the
S4 of the above section.
They are as follows: |
| |
| S4.1 |
= S4 + M13,
   pLppCMLpp or
M14. pLppCMLpp or
M14.    pLpLpCMLpLp pLpLpCMLpLp |
| S4.1.4 |
= S4 + M15,
   pLppCLMLpp pLppCLMLpp |
| S4.2 |
= S4 + M12,
 MLpLMp MLpLMp |
| S4.2.1
|
= S4.2 +
M13 |
| S4.3 |
= S4 + M11,
A Lpq Lpq Lqp Lqp |
| D (S4.3.1) |
= S4.3 +
M13 |
| S4.3.2 |
= S4 + M17, A LpqCMLqp LpqCMLqp |
| S4.3.3 |
= D + M20,
CLMpCLMqCMKpqLMKpq |
| S4.3.4 |
= S4.3.2 +
M20 |
| S4.4 |
= S4 + M16,
 pCMLpLp pCMLpLp |
| S4.9 |
= S4.4 +
M20 |
| |
= S4 + M21,
 CpLMpCCqLMqCMKpgLMKpq CpLMpCCqLMqCMKpgLMKpq |
| |
= S4.4 +
M18, ACMLppCLMqMLq |
| |
= S4 + M19,
A MLpLp MLpLp MLMqCqLq MLMqCqLq |
| V1 |
= S4 + M24,
ALpA pq pq pNq pNq |
| V2 |
= S5 + M24 |
| K1 |
= S4 + M22,
 LMpMLp LMpMLp |
|
K2 |
= S4.2 +
M22 |
| K3 |
= S4.3 +
M22 |
| K3.1 |
= D + M22 |
| K3.2 |
= S4.3.2 +
M22 |
| K4 |
= S4.4 + M22 |
| |
|
|
| (B.4) |
Modal sequent-logic for S1°-S5 |
| |
The modal sequent-logics are based on the logic LPC of section
A.2. The sequent-logics other than LS1°, LS2°, LT°,
LS3°, and LS4° (sequent-logics corresponding to the 'nought
systems') will have a rule to introduce L into the antecedent: |
| |
|
| |
The sequent-logics corresponding to the nought systems will lack this
rule, having only a rule to insert L into the succedent. Other
than this distinction between nought and nonnought systems, modal
sequent-logics will be distinguished by their ®L
rule, as follows: |
| |
|
| |
LS1
and LS1°: |
| |
|
| |
| 1. |
|
If G is singular or empty,
Q = G and D = a; |
| 2. |
|
In all other cases, D is empty and
Q has as its members two and only
two of the formulas belonging to G. |
|
| |
|
| |
LS2
and LS2°: |
| |
|
| |
®L may be applied with the sequence
G empty; however, if it is once so
applied, it may not be applied again at all in the same proof string. |
| |
|
| |
LT and
LT°: |
| |
Rule
®L
for these systems is as for LS2 and LS2°, but the
restriction is omitted. |
| |
|
| |
LS3 and
LS3°: |
| |
|
| |
| (a) |
Each formula of
LQ
is a subformula of a
or a subformula of LG or LD;
the left premiss is provable in LPC. |
| (b) |
Either
D or
G may be empty, but if
both of these sequences are empty,
rule ®L may not be applied again in the same proof string. |
|
| |
|
| |
LS4 and
LS4°: |
| |
|
| |
No
restrictions on G,
D. |
| |
|
| |
LS5: |
| |
|
D, LG
® LQ,
a |
|
|
®L |
|
LD,
LG ®
LQ,
La |
|
|
| |
Normal-form theorem not provable. |
| |
|
| (B.5) |
Sequent-logic for systems between S4
and S5 |
| |
Sequent-logics have been developed for several of these systems. The
normal-form theorem is in general not provable for these systems, so
CUT must be included in their formulations. |
| |
LS4.2: |
| |
Replace LS4's
®L
by: |
| |
|
D, LG
® LNLQ,
a |
|
|
®L |
|
LD,
LG ®
LNLQ,
La |
|
|
| |
|
| |
LS4.3: |
| |
Add the following sequent as an axiom schema to LS4: |
| |
LALab,
LAaLb ®
La,
Lb |
| |
|
| |
|
| |
LS4.4: |
| |
Axioms and rules involving the arrow ®
are as for LS4; in addition, another arrow
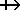 is
employed; axioms and rules for is
employed; axioms and rules for
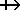 are
obtained by replacing ® in axioms
and rules of LS5 by are
obtained by replacing ® in axioms
and rules of LS5 by
 .
Sequents G .
Sequents G
 Q occurring in
proofs are called 'subtheorems'; only sequents involving the ordinary
arrow are theorems. Movement from subtheorems to theorems is by the rule
Q occurring in
proofs are called 'subtheorems'; only sequents involving the ordinary
arrow are theorems. Movement from subtheorems to theorems is by the rule |
| |
|
LG
 LQ
LQ |
|
|
CONV |
Q,
LG
 LQ
LQ |
|
|
| |
|
| (B.6) |
Tableaux for modal
systems |
| |
All these structures include MPC. Tableaux for the nought systems
(i.e. tableaux of the structures MS1°, MS2°, MS3°,
MS4°, and MT°) differ from those for other systems in that
the auxiliarity relation is not reflexive; tableaux are not auxiliary to
themselves. In the other structures discussed, this relation is
reflexive; this affects the application of the rules for L on the
left. We shall state rules asserting what to do when a formula La
occurs left or occurs right in a tableau. Distinguishing the system
MSn° from MSn depends on the difference noted
in their auxiliarity relation. |
| |
|
| |
MT° and MT: |
| |
For MT°, the only tableaux which must be auxiliary to a given
tableau are those constructed by an application of L-r in
that tableau; for MT in addition, each tableau is auxiliary to
itself: |
| |
| L-r: |
If La
occurs on the right of a tableau, construct a
new tableau auxiliary to that tableau and beginning with only
a on its right. |
| L-l: |
If La
occurs on the left of a tableau, write
a on the left of
each tableau auxiliary to that tableau. |
|
| |
|
| |
MS2° and MS2: |
| |
Structures for S2 and S2° will involve possible worlds of
a kind different from the ordinary, called 'non-normal' worlds, and so
also non-normal tableaux. Statements La
are always false in a non-normal world, and statements Ma
are always true. These structures are like MT° and MT
except for having the following instead of L-r above: |
| |
| L-r(2): |
When La
occurs on the right of a
(normal) tableau, split the alternative set
to which that tableau belongs; in one of the new alternative sets begin a
new auxiliary normal tableau with
a on its right; in
the other new alternative set, begin a new non-normal tableau with
a on its right. |
|
| |
|
| |
MS1°
and MS1 |
| |
These are of considerable complication, and the reader is referred to
the relevant place in Chapter 9. |
| |
|
| |
MS4° and MS4: |
| |
Here the accessibility and so the auxiliarity relation is transitive; to
reflect this, we alter rule L-l of MT° and MT
to read |
| |
| L-l(4): |
If La
occurs on the left of a tableau
t (of LS4° or LS4),
write both a
and La
on the left of each tableau auxiliary to t (unless, of
course, a formula to be written is already there). |
|
| |
|
| |
MS3° and MS3: |
| |
Replace rule L-l for MS2° and MS2 with: |
| |
| L-l(3): |
When La occurs on the left of a (normal)
tableau t, write both a and La
on the left of each normal tableau auxiliary to t (unless,
of course, the formula to be written already stands there). Write only a
on the left of each non-normal tableau auxiliary to t. |
|
| |
|
| |
MS5: |
| |
In
MS5 the accessibility and auxiliarity relations are reflexive,
transitive, and symmetrical. The rules employed are: |
| |
| L-r(5): |
If the formulas La, LQ
are all the formulas beginning with L on the right of a tableau,
create an auxiliary tableau beginning with a, LQ
on the right. |
| L-l(5): |
If La occurs left in a tableau t,
write a and La
left in every tableau ancestrally generated from t (unless
such formulas already occur there). |
|
| |
|
| |
MS4.2: |
| |
The accessibility relation here is 'convergent' as well as transitive
and reflexive. Replace L-r of MS4 by: |
| |
| L-r(4.2¢): |
When the formulas LNLQ, La are all the formulas beginning with L on the right of an
MS4.2¢
tableau, construct a tableau auxiliary to that tableau and having LNLQ
and a
on its right. |
|
| |
|
| |
MS4.3 |
| |
The accessibility relation here is reflexive, transitive, and linear.
Replace L-r in MS4 by |
| |
| L-r(4.3): |
Where La1,
. . ., Lan
occur on the right of an MS4.3 tableau, split that tableau into n
tableaux, each one having auxiliary to it a tableau with a different one of the
a1, . . ., an
on its right; the auxiliary tableau with ai
on its right, 1
£ i
£ n, will also
have the set of formulas La1, . .
., Lan less Lai
on its right. |
|
| |
|
| |
MS4.4: |
| |
Here the main and the auxiliary tableaux differ in kind: a rule for L-left
is given for main and for auxiliary tableaux respectively: |
| |
| L-l(4.4m): |
If La
occurs left in a main MS4.4 tableau, write La
and
a left in all tableaux
of that alternative set (except where they already occur). |
| L-l(4.4a): |
If La
occurs left in an auxiliary MS4.4 tableau, write La
and a
left in all auxiliary tableaux of that alternative set (except where they
already occur). |
|
| |
And in like manner, rules for L on the right, here for auxiliary
and for main tableaux respectively: |
| |
| L-r(4.4a): |
If La
occurs left in an auxiliary tableau in MS4.4, begin a new auxiliary
tableau with
a on its right. |
| L-r(4.4m): |
| (1) |
If La
occurs right in a main tableau and a
also occurs right there, no further action is taken with this La. |
| (2) |
If La1, . . ., Lam.
occur right in a main tableau and a1,
. . ., am all occur left
in that tableau, begin a new tableau auxiliary to the main and starting with
La1, . . ., Lam
on its right. |
| (3) |
If La1, . . ., Lan
occur right in a main tableau and none of the a1,
. . ., an. occur either left or
right in that tableau, split that tableau into n + 1 alternative
tableaux; a different one of the a1, .
. ., an will be written on the
right of each of n of these tableaux; all the a1,
. . ., an will be written on
the left of the (n + 1)th. |
|
|
| |
|