THE SYSTEMS OF COMPLETE
MODALIZATION -- BASIC SYSTEMS OF TABLEAUX
Tableaux for S4° and S4
WE shall now extend the work of
Chapter 9 as well as of Chapter 13 to develop
models for the completely modalized systems. As Chapter 9 began its studies with
the systems T° and T, so will this chapter begin with S4°
and S4. As was indicated in Chapter 9, the characteristic feature of
model structures for the systems of the current section is the fact that the
accessibility relation here will be transitive; thus we shall speak of model
structures MS4° and MS4 which have a transitive accessibility
relation. The accessibility relation in MS4, as in MT, will be
reflexive as well. The MPC rules and the rule L-r will be
the same here as for MT° and MT; note, though, that because of the
transitivity of the accessibility relation, any tableau bearing the ancestral
of the auxiliarity relation to a tableau tl will itself be
auxiliary to tl, and so will have formulas carried into it by
applications of rule L-l in tl. This is not true, of
course, in the general case for MT° and MT. Another way of looking
at the situation is to note that in situations in which the rule L-l
is to be applied creation of the countermodel demands that p be true in
every world accessible to the world (call it w1) corresponding to
the tableau tl in which the L-l is performed.
Suppose that p is false in some world w3 accessible to a
w2 which in turn is accessible to wl. By transitivity,
w3 is accessible to wl, and so Lp could not
hold in wl. If, then, Lp does hold in wl,
p must also hold in w3; more generally, if a world wx
has access to a world wy and Lp holds in wx,
then p must hold in every world accessible to wy as a part
of its holding in every one accessible to wx. The import of this
is that if Lp is to hold in wx, it must hold also in
wy and indeed, in every world accessible to wx. We may
then revise rule L-l for MS4° to read:
| L-l(4): |
If La
occurs on the left of a tableau
t (of LS4° or LS4),
write both a
and La
on the left of each tableau auxiliary to t (unless, of
course, a formula to be written is already there). |
As an example, let us consider the tableau construction beginning with
CLpLLp on its right. An application of C-r gives us Lp
left and LLp right; the LLp then causes the application of
L-r, generating an auxiliary tableau into which p and Lp
are inserted on the left by the new L-l.
This last tableau closes, and so the whole construction closes, and by
*9.1 CLpLLp is valid in LS4°, as will also be
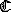 LpLLp. Since all the theses of
T° will be valid in the structure MS4° (which includes MT°)
and since
LpLLp. Since all the theses of
T° will be valid in the structure MS4° (which includes MT°)
and since 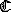 Lpp will be valid in
MS4, which has a reflexive accessibility relation, we assert:
Lpp will be valid in
MS4, which has a reflexive accessibility relation, we assert:
| *14.1 |
If a formula is provable in S4° (S4),
it is valid in MS4° (MS4). |
To prove the converse of *14.1, we shall make use of the
sequent-logics LS4° and LS4 of the last chapter. Just as in
Chapter 9, we shall view each sequent-logic proof
string as divided into segments, the first of which begins with an axiom and
each following one with an application of
®L; the
®L here,
however, is that of LS4°, which is
Suppose now that we have a construction of tableaux beginning with formulas
G
left and
Q
right in the main tableau. We then begin to use that construction as
a recipe for the writing of a sequent-logic proof just as indicated for MT° (MT)
tableau constructions in Chapter 9. Let us say that a tableau tx is
'immediately
auxiliary' to a tableau ty iff tx was created by an application of
L-r in ty
itself. The only difference between reconstruction of LT° (LT) proofs as in
Chapter 9 and LS4° (LS4) proofs as here lies in the way the formulas on the left
beginning with L are handled at the
®L
steps which mark the movement from one
proof string segment to the next. We shall recall that in an MT° (MT) tableau
construction, each auxiliary tableau tx is thought of as beginning with a
certain number of formulas
D
on its left and a formula
a
on its right. The formula
a
was inserted by L-r from the tableau ty to which tx
is auxiliary, and the
D
come from applications of L-l to the formulas LD
standing left in ty. The rule
®L
in LT° (LT) infers LD
® La
from
D
®
a
and
permits us to move from the proof string corresponding to tx to that
corresponding to ty. The auxiliary tableau tx in an
MS4° (MS4) construction,
however, will -- in the general case -- be able to be auxiliary to more tableaux than
just ty; it is immediately auxiliary to ty, but it is also auxiliary to any
tableau to which ty is auxiliary. And the rule L-l(4) for these model structures
means that the formulas inserted into tx by applications of L-l will not only be
the
D, as with MT°, but the sequence
D, LD, where the
LD
are all the formulas
beginning with L and on the left in all the tableaux to which tx is auxiliary.
Where tx had as its initial formulas in MT° (MT)
D
left and
a
right, in MS4°
(MS4) it begins with
D, LD
left and
a
right, where L-r in ty (to which tx is
immediately auxiliary) inserted the
a
from La
right in ty, and where LD
are all
and only the formulas beginning with L on the left of ty, regardless of
the tableaux in which the various formulas of LD
originally occur (that is, the
tableaux in which they first caused application of L-l(4)). The sequent
beginning the proof string segment corresponding to ty is then LD
®
La; that
ending the proof string segment corresponding to tx is
D, LG ® a. When, then,
we come to the point (in the construction of an LS4° (LS4) proof on the basis of
the recipe given by MS4° (MS4) tableaux) which corresponds to that in the
LT°
(LT) reconstruction from tableaux at which
®L
is applied, we find that we can
apply LS4°'s
®L
as required; the movement from tableau ty to tx in
MS4° (MS4) is
essentially from the formulas LD
left and La
right in ty to
D, LD
left and
a
right in tx. The inverse of that movement is the movement in LS4° (LS4) by
®L
from
D, LG ® a
(the last sequent of the segment corresponding to tx) to LD,
LD ®
La, which contracts to
LD ®
La, which may be considered the first sequent
of the segment corresponding to ty. LS4°'s
®L then gives us the inverse of
MS4°'s L-r, and so enables us to extend our 'recipe' for constructing
sequent-logic proofs to these systems. We note that LS4 will have just the same
relation to MS4 as LT does to MT, and so we shall be able to assert (taking
*14.1 into consideration):
| *14.2 |
A formula is valid in MS4° (MS4) iff it is provable in LS4° (LS4). |
By *9.2, then:
| *14.3 |
MS4° (MS4) provides a decision procedure for S4° (S4). |
Tableaux for S3° and S3
The original work on tableaux for S4 appears in
Kripke 1963; his formulation there differs
somewhat from ours; Kripke 1965a contains
a formulation for S3 tableaux; here we present a somewhat different
formulation along with one for S3°. It will be recalled that the S2°
model structure differs from that for T° by containing provision for
'non-normal worlds'. The non-normal world is one which behaves normally so far
as PC operations are concerned, but which acts as if it had access to the
'impossible possible world', in which every statement would be both true and
false, with the result that every statement beginning with an L in a
non-normal world is false, while every one beginning with an M is true.
Model structures for S3° (S3) will behave like a cross between
those for S4° (S4) and those for S2° (S2). The
accessibility relation for MS3° (MS3) will be transitive as is
that for MS4° (and that for MS3 will also be reflexive), but these
model structures will include non-normal worlds just as did those of MS2°.
MS3° will have, as will MS3, the operations of MPC and the
rule for L on the right will be as for MS2°:
| L-r(2): |
When La
occurs on the right of a
(normal) tableau t, split the
alternative set to which that tableau belongs; in one of the new
alternative sets having a new normal tableau auxiliary to t
and beginning with
a right, and the other having a non-normal
tableau auxiliary to t and beginning with
a right. |
The rule for L on the left shall be new:
| L-l(3): |
When La occurs on the left of a (normal)
tableau t, write both a and La
on the left of each normal tableau auxiliary to t (unless,
of course, the formula to be written already stands there). Write only a
on the left of each non-normal tableau auxiliary to t. |
As the last clause of the above indicates, transitivity does not extend to
the accessibility relation for non-normal tableaux -- as well it
should not. As an example, we test the formula CLLpLLLp;
first we apply C-r giving us LLp left and LLLp
right:
Rule L-r dictates that we split the alternative set, as
indicated above; the left of the tableaux in the split will take a non-normal
and the right a normal auxiliary tableau, each beginning with LLp right:
As the above diagram shows, we have also carried out the injunction of
L-r(3) to insert LLp and Lp left in the normal auxiliary
tableau and just Lp left in the non-normal one. The normal auxiliary
closes by virtue of having the same formula (LLp) both left and right;
the non-normal auxiliary closes as S2° non-normal tableaux can -- by
having La,
whatever
a
may be (here
a
= p), on its left. The whole construction then closes, and CLLpLLLp
is valid. Note that if we had started out with CLpLLp instead, the normal
auxiliary tableau would close, but the non-normal one would be
which does not close and so gives us a countermodel. As another example,
consider the construction which begins with CLCpqLCLpLq on the right of
the main tableau. Again, C-r gives us LCpq left and
LCLpLq right, and rule L-r(2) instructs us to split
and begin the non-normal tableau below the split tableau (here on the left)
as well as the normal tableau below the other split tableau both with CLpLq
on the right. Rule L-l(3) now tells us to put LCpq and
Cpq left in the normal tableau and to put Cpq only left in the
non-normal one; the rule C-r now tells us to place Lp left
and Lq right -- we execute this for the non-normal tableau
We note that the non-normal tableau has Lp on
its left and so will close. The normal tableau has LCpq on its left and
CLpLq on its right; an examination of the rules for L will show
that in this situation they will behave just as do the L rules for
MS2°, resulting in the closing of the normal tableau (just as an MS2°
tableau beginning with LCpq left and CLpLq right will close). The
whole construction then closes, meaning that CLCpqLCLpLq is valid in
MS3° (MS3). We note that since this formula has as its antecedent
beginning with an L, the construction beginning with
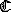 LCpqLCLpLq will also close.
And, as we have indicated, examination of L-l(3) (MS3°
al-ready has L-r(2)) will show that any formula valid in MS2°
(MS2) will be valid also in MS3° (MS3). Since S2° (S2)
plus LCLCpqLCLpLq gives S3° (S3), we have:
LCpqLCLpLq will also close.
And, as we have indicated, examination of L-l(3) (MS3°
al-ready has L-r(2)) will show that any formula valid in MS2°
(MS2) will be valid also in MS3° (MS3). Since S2° (S2)
plus LCLCpqLCLpLq gives S3° (S3), we have:
| *14.4 |
If a formula is a thesis of S3° (S3), then it is valid in
MS3° (MS3). |
As we have done with similar metatheorems, we now set about proving the
converse of the above. Once again, we make use of the sequent-logics we have
developed. A construction in MS3° (MS3) is like one in MS4°
(MS4) except for the alternative splits at the L-r
applications and the resulting non-normal tableaux. The differences in the
L-l rules for the systems pertain only to non-normal tableaux. The
alternative sets which contain only normal tableaux, then, provide us with a
recipe for the construction of an LS4° (LS4) proof of the sequent
corresponding to the initial state of the tableau construction. But at each
L-r in the construction we also have a non-normal tableau, which --
in a closing construction -- must itself close. We wish to show that whenever a
closing MS3° (MS3) normal tableau t1 is auxiliary to
a tableau t2 and
G, LG ® a
is the last sequent of the proof segment corresponding to t1
(making LG
® La the first
sequent of the LS4° (LS4) segment corresponding to t2)
we shall be able an the basis of the non-normal tableau generated at the same
time as was t1 to show that G ® LQ,
a is provable in LS3° (LS3) and so that LG
® La is provable by the
®L of LS3°. This
non-normal tableau closes, and it closes either by having a formula
b
on both sides of it, or by having a formula Lg
located on its left. Suppose the former. Then we note that by L-l(3)
the non-normal tableau will have the formulas
G
on its left, and by L-r(2),
a
on its right. Since it closes like an LPC tableau, we shall have G ® a
provable in LPC, and so G ®
LQ, a also so provable.
But then this provides us with a left premiss for
LS3°'s ®L as required.
Suppose now that the non-normal tableau closes by having Lg
on its left. This means that the same tableau, if it had Lg
on its right also would be a closing LPC tableau. This means further that
the sequent G ® Lg,
a
is a theorem of LPC and so of LS3°. But then let Lg
be one of the LQ
and G ® LQ,
a
is provable; note that the requirements of LS3°'s
®L are met in that Lg
is indeed a subformula of
a
or of one of the formulas of
G. This all means that if a construction in
MS3° (MS3) closes, the LS4° (LS4) proof
constructible on the basis of the normal alternative sets of the construction
has each of its ®L steps as a
®L of LS3° as well, and
so is also an LS3° (LS3) proof. By *14.4 and *9.1,
then, we have
| *14.5 |
A formula
a
is valid in MS3° (MS3) iff ® a
a is provable in LS3° (LS3), and so also iff
a
is a thesis of S3° (S3). |
By *9.2, then
| *14.6 |
MS3° (MS3) provides a decision procedure for S3° (S3). |
Tableaux for S5
The very first of the Lewis modal systems to have a 'possible worlds'
semantics provided for it was S5, in
Kripke 1957. Our formulation differs somewhat from Kripke's, but it makes
use of the fact, as his did, that the accessibility relation in model structures
corresponding to S5 is symmetrical as well as transitive and reflexive.
We note once more that there is no S5°; in Chapter 11 we showed that the
addition of 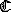 MLpLp to S1°
makes
MLpLp to S1°
makes 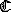 Lpp and
Lpp and
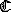 pMp provable. Paralleling this
in the model structures of the present section is the obvious fact that if the
accessibility relation is transitive and symmetrical and there is any accessible
world, then the relation must be reflexive as well. Indeed, in a model in which
the accessibility relation has these properties, every world will have access to
every world; in a sense there is no one real world in such a model except by
arbitrary designation (or, one might prefer to say, by an application of the
axiom of choice).
pMp provable. Paralleling this
in the model structures of the present section is the obvious fact that if the
accessibility relation is transitive and symmetrical and there is any accessible
world, then the relation must be reflexive as well. Indeed, in a model in which
the accessibility relation has these properties, every world will have access to
every world; in a sense there is no one real world in such a model except by
arbitrary designation (or, one might prefer to say, by an application of the
axiom of choice).
Kripke expressed the transitive-symmetrical nature of the accessibility
relation in his tableaux for S5 in terms of true formulas; that is, his
L-l rule takes account of the fact that if a formula La
is to be true in any S5 possible world, then
a
must be true in every S5 possible world (because every world has access
to every world). The rule L-l would then call for the insertion of
a
on the left of every tableau of that construction. As an
example let us try a construction beginning with CMLpLp on the right of a
tableau; C-r first gives us MLp left and Lp right,
and N-l then gives us LNLp right (MLp = NLNLp)
The rule L-r in the Kripke formulation now calls for us to
create two auxiliary tableaux, one beginning with p right and one
beginning with NLp right
We have applied N-r in the right one of these two. It is clear
that if the above were an MS4 construction, say, that we should have
reached the end of the line; it would give us a countermodel to CMLpLp.
In an S5 construction like this, however, every tableau is auxiliary to
every other, in effect. In particular, we are interested in the accessibility of
the tableau beginning with p right to the one beginning with NLp
right; rule L-l commands us to write p on the left of the
former as a result of the Lp left in the latter:
The result is a closing tableau construction and the validity of CMLpLp.
We may call this model structure for S5 as formulated by Kripke MS5.
We clearly have, with the above:
| *14.7 |
If a formula is provable in S5, it is valid in MS5. |
We note at this point that if La
is false in any MS5 world, then it is false in all. We may then consider
that this gives us permission under MS5's L-r to write La
right in any MS5 tableau when it occurs right in one. We shall use this
later.
We shall find it convenient also to take a somewhat different approach to
S5 semantics, an approach which emphasizes the role of falsehood of formulas
rather than their truth. What we shall take advantage of is the fact that if a
formula La
s false in any SS world, then it must be false in every S5 world -- this
again is dictated by the mutual accessibility of these
worlds. We shall reflect this orientation in a model structure MS5¢;
first of all, the tableau operations of LPC will apply in this structure.
The version of L-l will be much like that for LS4, but we
shall require a variation in terminology for our statement of it for MS5¢.
We note that in MS5 formulas can be inserted by L-l into a
tableau tx from a tableau ty in spite of the fact
that tx, while auxiliary to ty, was not 'ancestrally
generated' from ty by rule L-r. We shall say that a
tableau tx is ancestrally generated from a tableau ty
if it is ty or is created by an application of L-r
in ty or in a tableau ancestrally generated from ty.
We then state:
| L-l(5): |
If La occurs left in a tableau t,
write a and La
left in every tableau ancestrally generated from t (unless
such formulas already occur there). |
We also shall employ the following version of L-r:
| L-r(5): |
If the formulas La, LQ
are all the formulas beginning with L on the right of a tableau,
create an auxiliary tableau beginning with a, LQ
on the right. |
The
a
on the right in the new tableau reflects the fact that, as in all these systems,
a
must be false in some world accessible to the original world. The LQ
right in the new tableau reflect the S5 semantic characteristic of
'if not-necessary in one world, then not-necessary in all worlds'. Let us now
test the formula CMLpLp in MS5¢;
the original tableau will be just as in the Kripke formulation MS5 above;
by our L-r(5), however, we create one auxiliary tableau with
NLp and Lp right; an application of N-r then places
Lp left in that tableau:
Our construction then closes. We might also have tried to carry out this
construction by creating a new tableau with p and LNLp right; as
it turns out, this route gets us nowhere -- which matters not, for the way we
did choose results in the contradiction shown in the above tableau construction.
For reasons that will become clear, we shall find it necessary to include in
the basis of MS5 a further rule, of a kind different from
those we have heretofore considered. This rule involves an
alternative split, and is actually a correlate of the sequent-logic rule cut:
| |
At any time, an MS5¢ alternative set may
be split, with the resulting alternative sets identical except for having
a new formula
a
on the left of one of the tableaux of one of the sets and on the right of
the corresponding tableau of the other set. |
This rule may be intuitively justified by noting that
a
will be either true or false in any world, and specifically in the world
corresponding to the tableaux in which a was inserted. It is clearly the inverse
of cut; we note that where cut eliminates formulas which were introduced in a
proof so that they do not appear in the end sequent, this rule adds a formula
which did not appear in the original inventory of the main tableau.
It should be clear that all the theses of S4 will be valid in MS5¢
and that the rules of that system are validity-preserving in that system (the
rules of MS4 are included in those of MS5¢).
Since CMLpLp and -- by application of L-r --
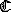 MLpLp are valid in MS5¢,
we may then assert:
MLpLp are valid in MS5¢,
we may then assert:
| *14.8 |
If a formula is a thesis of S5, it is valid in MS5¢. |
As in the preceding sections of this chapter, we shall prove the converse of
the above by means of a sequent-logic, LS5. When we set down LS5
in the last chapter, we noted that the normal-form theorem was not provable for
it. This, however, does not prevent its being a useful bridge between S5
and its semantics. We recall that LS5 is like LS4 except for
having as its
®L
rule:
|
D, LG
® LQ,
a |
|
|
®L |
|
LD,
LG ®
LQ,
La |
|
It is clear that this rule bears precisely the same relation to the L-r(5)
of MS5¢ as does the
®L
of LS4 to the L-r of MS4. We note that where the
'cut-like' special rule for MS5¢ is used in a
construction, the rule cut would be employed in the corresponding LS5
proof. With this in mind and altering the proof of *14.2 to refer to the
®L
of LS5 and the rule L-r for MS5¢
rather than the corresponding rules of LS4 and MS4, we get:
| *14.9 |
A formula a is valid in MS5¢ iff
® a
is provable in LS5 and so also iff
a
is a thesis of S5. |
The above result is made possible by the fact that the
'direction of generation' of tableaux in MS5¢
is antisymmetrical -- formulas are entered into tableaux only from tableaux
which are their 'ancestral generators' unlike the procedure in MS5.
Tableau constructions in MS5¢, then, can be
placed in correspondence with proofs in LS5, whose direction of
generation is also antisymmetrical.
The system MS5¢ has the advantage of
offering us a very easy correlation between the realm of S5 proof and
that of S5 models. It does this, as noted, by maintaining an
antisymmetrical generation of tableaux. But this antisymmetrical generation is
not coincident with the relation of auxiliarity as has been the generation of
tableaux in model structures studied up until this point. Thus we reach certain
points in which the rules for L in MS5¢
are inadequate to place formulas in certain tableaux in which they must occur by
the auxiliarity relation; as an example, note the construction begun for the
formula CMLpp, which is an S5 thesis and so must be valid in
MS5¢
After these preliminaries of applying the LPC C-r and
N-l, we use MS5¢'s L-r
and then, in the new tableau, N-r:
Since every world in this model structure must have access to every other
world, we should be able to write Lp and p left in the upper
tableau, for they must, by this accessibility relation, be true in the world
corresponding to this tableau. This would result in that tableau's closing. But
since the L-l of MS5¢ operates
in the antisymmetrical way noted, we cannot do this. The key to our problem here
is the cut-like rule we earlier mentioned as in MS5¢.
We note that Lp and p will have to be true in the world
corresponding to the main tableau for creation of a countermodel, and so we must
consider what happens in that situation; we then use the cut-like rule to split
the construction, writing Lp left (and so making p writable) in
the main tableau of one of the alternative sets resulting from the split; and
right in the main tableau of the other,
It will be noted that an application of L-l within the main
tableau having Lp left will place p left in that tableau, and so
will make that tableau close. The assumption that Lp is true in the main
tableau then yields a contradiction. On the other hand, if in the other tableau
we let LNLp be the La
of MS5¢'s L-r, we generate an
auxiliary tableau as follows:
Lp is carried along as the member of LQ;
an application of N-r in this auxiliary tableau gives us Lp
left as well as right, a closing situation, and the entire construction closes.
We then might use the construction as a recipe for the construction of an LS5
proof; the proof that would be so constructed appears almost in its entirety in
the last chapter as the proof of the sequent ®
LNLp, p. It is clear that the non-coincidence of ancestral generation and
auxiliarity is directly analogous to the non-provability of the normal form
theorem in LS5. And we shall find similar correlations in other modal
systems in which the auxiliarity relation (accessibility relation) makes
necessary different ordering of tableaux (worlds) from that required to obtain
between steps in a sequent-logic proof.
The model structure MS5 does not have this drawback. The insertion of
formulas from one tableau to another coincides with its auxiliarity relation,
and so it comes within the scope of *9.1 without the use of a cut-like
rule; further, the absence of such a rule brings it under *9.2 as well,
meaning that if S5 is complete with respect to MS5, then MS5
provides a decision procedure for S5. To establish this we shall have to
show that:
| *14.10 |
If a formula is valid in MS5, then it is valid in MS5¢. |
The problem of proving the above arises when a formula La
occurs on the left of an MS5 tableau which is not the main tableau. If no
such formula occurs in a construction, we can clearly parallel the construction
in MS5¢, with the latter construction closing
when the former does. Suppose that whenever no more than
k formulas beginning with L and located on the left occur in an
MS5 construction which closes, a closing construction for the original
formula for which the construction was begun holds also in MS5¢.
Consider the case in which there are k + l such formulas; note one of
these formulas, say La.
The main tableau in the MS5 construction must have La
and
a
inserted left in it by rule L-l. Instead of applying this rule to
insert La
and
a
into the main tableau, split the alternative set in which the main tableau
occurs, placing La
left in the main tableau of one of the resulting sets and right in the main
tableau of the other. This procedure may be justified by the inclusion of LPC
in LS5. By L-l
a
will also be left in the main tableau having La
left; indeed, by this rule La
and
a
may be written left in each tableau of this alternative set. But this
alternative set is now like the original in all respects and so closes just as
the original did. Since La
and
a
were inserted left in the tableaux of this new alternative set by virtue of an
La
in the main tableau, however, there are only k applications of L-l
needed in tableaux not the main tableau. This set then comes under the induction
hypothesis of the main induction, and there is an MS5¢
closing construction beginning with the same formulas now in the main tableau of
this alternative set (that is, beginning with the formulas with which the
original construction began, plus La
left in the main).
Now consider the alternative set in which La
was written right in the main tableau. As we noted (immediately subsequent to
the statement of *14.7), the reflexive-transitive-symmetrical property of
MS5's accessibility relation means that if La
is false in one world, then it is false in all. This means that with La
right in the main tableau of this set, it may be written right in any tableau of
this set, including the one which originally had on its left the offending La,
the one causing the introduction of La
and a into the main tableau. This set then closes by having La
left and right in that tableau, and it closes without the offending L-l,
falling then under the induction hypothesis. But then a closing MS5¢
construction beginning with the same formula as the original MS5
construction plus La
right is constructible, as well as a closing MS5¢
construction (as shown above) beginning with that same formula plus La
left. But then by the cut-like rule of MS5¢ a
closing construction beginning with the same formula as did the original MS5
construction is available, and so *14.10 holds, and we have, by *14.8,
*14.9, *14.10, and *9:1:
| *14.11 |
A formula a
is valid in MS5 iff it is valid in MS5¢
and so also iff ® a a is provable in
LS5 and so also iff a
is a thesis of S5. |
By the above and *9.2
| *14.12 |
MS5 provides a decision procedure for S5. |
![]() LpLLp. Since all the theses of
T° will be valid in the structure MS4° (which includes MT°)
and since
LpLLp. Since all the theses of
T° will be valid in the structure MS4° (which includes MT°)
and since ![]() Lpp will be valid in
MS4, which has a reflexive accessibility relation, we assert:
Lpp will be valid in
MS4, which has a reflexive accessibility relation, we assert:![]() LCpqLCLpLq will also close.
And, as we have indicated, examination of L-l(3) (MS3°
al-ready has L-r(2)) will show that any formula valid in MS2°
(MS2) will be valid also in MS3° (MS3). Since S2° (S2)
plus LCLCpqLCLpLq gives S3° (S3), we have:
LCpqLCLpLq will also close.
And, as we have indicated, examination of L-l(3) (MS3°
al-ready has L-r(2)) will show that any formula valid in MS2°
(MS2) will be valid also in MS3° (MS3). Since S2° (S2)
plus LCLCpqLCLpLq gives S3° (S3), we have:![]() MLpLp to S1°
makes
MLpLp to S1°
makes ![]() Lpp and
Lpp and
![]() pMp provable. Paralleling this
in the model structures of the present section is the obvious fact that if the
accessibility relation is transitive and symmetrical and there is any accessible
world, then the relation must be reflexive as well. Indeed, in a model in which
the accessibility relation has these properties, every world will have access to
every world; in a sense there is no one real world in such a model except by
arbitrary designation (or, one might prefer to say, by an application of the
axiom of choice).
pMp provable. Paralleling this
in the model structures of the present section is the obvious fact that if the
accessibility relation is transitive and symmetrical and there is any accessible
world, then the relation must be reflexive as well. Indeed, in a model in which
the accessibility relation has these properties, every world will have access to
every world; in a sense there is no one real world in such a model except by
arbitrary designation (or, one might prefer to say, by an application of the
axiom of choice).![]() MLpLp are valid in MS5¢,
we may then assert:
MLpLp are valid in MS5¢,
we may then assert: