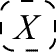
IN the Introduction, we showed that the "gamma part" of the Existential Graphs had a place near to the very heart of C. S. Peirce. Gamma as Peirce envisioned it was a system of many signs, of great complexity. Primarily, it was to be the system which, by using a book of sheets of assertion rather than just one, was to add an "extra dimension" to the logical analysis of reality; gamma was to help us extend this analysis to possible universes of discourse and to enable us to deal with problems beyond the scope of alpha and beta.
Hopes for the stereoscopic gamma went a-glimmering. Peirce was not able to pull the system together as he wanted to. But he did try to make a start; we restate here a passage we quoted in the Introduction:
In endeavoring to begin the construction of the gamma part of the system of existential graphs, what I had to do was to select, from the enormous mass of ideas thus suggested, a small number convenient to work with. It did not seem to be convenient to use more than one actual sheet at one time; but it seemed that various different kinds of cuts would be wanted (4.514).
The "different cut" to which Peirce seems to have paid most attention is the "broken cut," which we will recall from the Introduction. This is., in fact, the only of the gamma cuts to which any real attention is paid in the writings of Peirce appearing in the Collected Papers. The bulk of this chapter will be devoted to a study of systems including the broken cut among their signs.
In 4.516, Peirce states two rules for the use of the broken cut; one of these rules is our 0.13 of the Introduction. The other rule has two clauses and is stated as our 0.14 and 0.15 in the Introduction. We may at this point repeat these rules as we stated them here:
| 0.13 | In a broken cut already on SA any graph may be inserted. |
| 0.14 | A broken cut in an area enclosed by an odd number of cuts (which may be either alpha or broken cuts) may be transformed to an alpha cut (by "filling in" the breaks in it). |
| 0.15 | An alpha cut in an area enclosed by an even number of or by no cuts may be transformed to a broken cut (by erasing parts of it). |
At this point we shall simply remark that these rules are open to amplification and interpretation, as we shall eventually see; and depending on how we amplify and interpret, they will yield us a variety of logical systems. In this they are like the rule of "strict implication introduction," for example, which is used by Anderson and Johnstone(n1) to set up a system of natural deduction which is basically equivalent to the Lewis-modal S4. Although the rule as they present it enables us to derive the theorems of S4 within their system, there would be no trouble in so modifying the restrictions on the application of the rule as to enable us to derive the theorems of, say, the system S5.
We shall, then, construct several "broken cut" systems by slightly modifying certain rules for transformations involving the broken cut. As we will recall from the Introduction, the graph
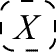
may be interpreted as asserting, "It is possibly not the case that X." Systems containing the broken cut among their signs, then, may be considered systems of modal logic.
In chapters I and II we compared the alpha and beta systems to ordinary logical calculi. The project for gamma will be similar. We shall compare the broken cut systems which we will define with ordinary systems of modal logic. We shall define four different broken cut systems, and shall compare them to four different standard modal systems. Three of the systems we shall thus use belong to the family of "Lewis-modal" systems, the "classical" modal systems of contemporary logic. The fourth system is a rather unusual modal system invented by Łukasiewicz .
The usual axiomatizations of modal systems ordinarily take either "necessity" (with 'Lp' read as "necessarily p" ) or "possibility" (with 'Mp' read as "possibly p") as primitive modal operators. Since the primitive modal operator in the gamma systems is the broken cut, which states "possibly not,'' it may be worthwhile to provide axiomatizations of our ordinary modal systems taking "possibly not" as primitive rather than the usual "possibly" or "necessarily." We thus shall state some rather neat axiomatizations of several Lewis-modal systems taking "possibly not" as primitive -- these are, so far as I am aware, new bases for these systems.
We shall then present the axiomatic basis for that unusual system of Lukasiewicz, and then make some remarks about that calculus.
The next step will be to describe each of the four broken cut systems we have mentioned, and to compare each in turn to an appropriate standard modal system. We shall, in fact, show that our broken cut systems are equivalent to these standard systems in the same sense that alpha, say, is equivalent to the CPC.
3.1 Remarks on Some Standard Modal Systems
If the alpha cut is to be considered a negation sign, then the broken cut will be a sign that states "possibly not.'' The broken cut then represents a "weak negation." We shall presently be comparing the systems involving the broken cut to certain standard modal calculi. As we mentioned, these systems are ordinarily formulated using either 'M' (possibility) or 'L' (necessity) as a primitive modal operator. It is easily possible, however, to get nice axiomatizations of the standard modal systems with which we will be concerned using "possibly not" as the only primitive modal concept. We may read 'Rp' as "possibly-not p." Then we have
| Definitions: | |||||||||||||||
|
|||||||||||||||
| Rule of Inference: | |||||||||||||||
|
|||||||||||||||
| Stock of Axioms: | |||||||||||||||
|
The axioms and rule will be considered to be subjoined to a complete CPC base, including the rules of detachment and substitution of variables. The specific formulations of the systems are as follows
| For each of the systems below, any complete base for the CPC. Also for each of these systems, the rule "RL" mentioned above. In addition, the axioms for the respective systems from the above stock are: | ||||||||
|
In what follows, we will allude to "well-known" axiomatizations of the above systems, in general, those developed by E. J. Lemmon.(n1)
At this point I shall also remark that although we will develop no broken cut system analogous to the calculus T, we include its axiomatization in 'R' here as a matter of general interest.
The axioms are, in general, quite expressive of the nature of 'R' as a sign of "weak negation." Axiom 2 indicates that this weak negation of a statement follows from the ordinary negation; this axiom is equivalent in deductive power to the theses 'CLpp' and 'CpMp' . Axioms 1, 1¢, and 1¢¢' are "laws of transposition" for the weak negation, analogous to ordinary PC laws of transposition like ' CCNpNqCqp' . By applications of appropriate CPC laws and the definition of 'L' , axiom 1 becomes 'CLCpqCLpLq', and axiom 1¢ becomes 'CLCpqLCLpLq'. It is well-known that CPC, RL, and the two theses:
| *1. | CLCpqCLpLq | |
| *2. | CLpp |
together are an axiomatic basis for the system T, while a replacement of above by
| *1¢. | CLCpqLCLpLq |
yields the system S4. Our axioms 1 and 1¢, again-, are easily shown to be theses of T and S4 respectively. We may state without hesitation, then, that the axioms in 'R' as we have given them form bases for T and S4. The system S4.2 is ordinarily formulated by subjoining the formula 'CMLpLMp' to a basis sufficient for S4; our axiom 3 is definitionally equivalent to this last formula, so we have also provided a sufficient base for S4.2.
The iterated modality 'RR' is equivalent to 'ML' ("possibly-not possibly-not" is the same as "possibly necessarily"). With this in mind, and transposing the consequent of 1¢¢, 1¢¢ becomes:
| *1¢¢. | CMLCpqCLpLq |
This latter formula is, of course, also easily transformable back into 1¢¢. If *1¢¢ is a thesis of a system, and *2 is also a thesis, then *1 is easily provable. Now substitute 'Cpp' for 'p' in *1¢¢; the result is:
|
4. |
CMLCCppqCLCppLq |
By PC and RL, the following strict equivalence holds:
|
5. |
LEqCCppq |
By PC and the substiitutivity of strict equivalence, which holds in the system containing PC, RL, and *2, all of which we have, and using the strict equivalence at 5, 4 becomes
|
6. |
CLCppCMLqLq; |
detaching now with the thesis 'LCpp' , which holds in all Lewis-modal systems, we get:
|
7. |
CMLqLq. |
This is a characteristic reduction formula for S5, the strongest of the Lewis-modal systems; CPC, RL, *2, and 7, in fact, constitute a standard axiomatic base for S5. The formula *1¢¢
is itself an S5 thesis, and easily shown to be such. It follows, then, that CPC, RL, *1¢¢, and *2 form a sufficient base for S5; and then so too will CPC, RL, 1¢¢, and 2 -- our axioms in 'R' -- as we stated earlier.
Of the systems for which we have provided "R-primitive" bases, we shall be interested in the relationship of S4, S4,2, and S5 to the broken cut systems. We shall also be concerned with one other modal system in this connection, and a rather unusual system at that. This is the ''Ł-modal" system of Łukasiewicz.(n1) It should be pointed out that this is not the fairly well-known "three-valued" modal logic of Łukasiewicz, but a system based on his PC extended to include functor-variables, which we mentioned in chapter I. We will not, however, consider the system as we state it to include primitive functor variables; "formulas" like 'CpCd1
dp', for example, will be considered theorem-schemata rather than theorems. It is clear that for every theorem containing functor variables in the system as Łukasiewicz states it, there will be an identical-appearing theorem schema of the system as we state it. The Ł-modal system contains the rules of detachment and substitution for variables, and has as axioms|
8. |
|
|
|
9. |
CLpp |
with standard definition "M =df NLN" ; this is the system with 'L' primitive. It might also be stated with 'M' primitive, or even with 'R' primitive: Lukasiewicz also lists two "axiomatic rejections" for the system:
| *CpLp | ||
| *NLp |
These will not be of too much interest for our purposes, for they do not actually enter into the generation of the set of theorems of the system.
The system as stated looks innocuous enough, but there is one catch. Functor signs, like '
d' in 8, may stand in place of any context whatsoever, including modal contexts. This causes some unusual results; the formula| 10. | CLCpqCpLq, |
for example, is a thesis of the system. This formula could not be a thesis in
any of the Lewis-modal systems, for they all contain as a law 'LCpp',
which in the presence of 10 would yield as a theorem 'CpLp', and
thereby destroy the modal nature of the system. Ł-modal, however, contains no
thesis of the form
![]() L
L
| 11. | CMpMLp, |
which are also incompatible with many characteristic Lewis-modal theses. This last is a reduction formula, but it differs from, say, the reduction theses of S5. Where the S5 reduction formulas "reduce" a string of modal operators to the rightmost member of the string, as indicated by 7, the Ł-modal reduction theses reduce such a string to the leftmost member, as indicated by 11. As an example, 'MLLMMMLMLp' is equivalent in S5 to the simple 'Lp', while in Ł-modal it is equivalent to 'Mp'.
3.2 The Broken Cut Systems
We now turn our attention back to the broken cut. Earlier in this chapter, we repeated from the Introduction the rules 0.13, 0.14, and 0.15 for the use of the broken cut. There is not too much doubt about how the latter two of these rules are to be interpreted and applied; 0.13,
| 0.13 | In a broken cut already on SA any graph may be inserted. |
however, begs for study. The question raised by 0.13 is this: Just what is to be the over-all function of the alpha rules of transformation in a system containing the gamma cut? For example, the transformation
|
|
® |
|
would involve the iteration of a graph "across a broken cut." Do we wish to permit such transformations at all? Do we wish to permit them with certain restrictions? Or do we wish to permit them in unlimited fashion? The rule 0.13 is in itself a very limited rule, as it is stated. But it does involve a certain "cross-breeding" of alpha and gamma concepts. Although it is really just a weak "gamma-version" of our alpha Rins, it somewhat coercively turns our attention to the question of alpha and gamma "cross-breeding" in the rules in general.
Well, we now propose to open an experimental farm for the investigation of some of the possible hybrids, and for the comparison of them with some of the earlier mentioned standard breeds of modal logic. I think we shall find the alpha-gamma progeny, unlike most hybrids, relatively fertile.
3.21 Gamma-MR: Broken Cuts with Minimal Restrictions
The first broken cut system we shall develop and study is one which allows the most liberal possible interpretation within gamma of the alpha rules of inference; we shall call this system "Gamma-MR." The basis for Gamma-MR will be as follows:
The single axiom for Gamma-MR will be b, the blank alpha SA.
The rules Rins and Rers will apply just as they do in alpha, and for purposes of their application, broken cuts will be counted as if they were alpha cuts to determine "oddness" or "eveness" of enclosure.
The rules Ritr and Rdit will apply just as they do in alpha; any graph may be iterated (or deiterated), across any kind of cut or combination or cuts, just as if they were alpha cuts.
The rules Rbcl and Rnbc may be applied just as they are in alpha, in any area at all. But it is understood that the only cuts that may be inserted or removed by these rules are alpha cuts.
In addition, there shall be two other rules which shall apply in this system; these rules correspond to our 0.14 and 0.15.
| Rgam(Y, X): | Which is true iff X contains., in an area enclosed by an even number of or by no cuts of either kind or in any mixture, an alpha cut, and Y is like X except for having at that position a broken cut rather than an alpha cut. | |
| Rngm(Y, X): | Which is true iff Rgam(S(X), S(Y)) is true. |
Before we go any further, let us state -- without explicit proof, however -- two theses which will be useful in what follows. These theses will be analogs for our modal systems of lemmas 1.03 and 1.04:
| *3.01 |
|
||
| *3.02 |
|
The formula 'p
![]() q',
of course, is read, ''p strictly implies q''; it is equivalent; to
the formula -- in Polish notation -- 'LCpq'. The notation used above is
used simply for the sake of consistency with that of lemmas 1.03 and
1.04. We may assume that the systems for which these theses are stated are "L-primitive')
systems; and 'L' affects the A-pos or C-pos of subformulas in its scope
in no way. The theses above are provable by an induction on the number of L's
(belonging to the formula QA(B) or QC(B))
within whose score B is located. But without going through the tedium of an
explicit proof, I submit that the theses are intuitively quite acceptable.
Recall the relationship of lemmas 1.03 and 1.04 to the rule of
substitutivity of material equivalence in CPC. It may then help our intuition if
we note that substitutivity of material equivalence holds in the Ł-modal
system, while substitutivity of strict equivalence holds in all the
Lewis-modal systems. That the above theses would hold in "M-primitive" or
"R-primitive" systems is evident. Just note that since ERpNLp, an
R will affect the A-pos or C-pos of formulas in its scope just as if it
were an 'N'.
q',
of course, is read, ''p strictly implies q''; it is equivalent; to
the formula -- in Polish notation -- 'LCpq'. The notation used above is
used simply for the sake of consistency with that of lemmas 1.03 and
1.04. We may assume that the systems for which these theses are stated are "L-primitive')
systems; and 'L' affects the A-pos or C-pos of subformulas in its scope
in no way. The theses above are provable by an induction on the number of L's
(belonging to the formula QA(B) or QC(B))
within whose score B is located. But without going through the tedium of an
explicit proof, I submit that the theses are intuitively quite acceptable.
Recall the relationship of lemmas 1.03 and 1.04 to the rule of
substitutivity of material equivalence in CPC. It may then help our intuition if
we note that substitutivity of material equivalence holds in the Ł-modal
system, while substitutivity of strict equivalence holds in all the
Lewis-modal systems. That the above theses would hold in "M-primitive" or
"R-primitive" systems is evident. Just note that since ERpNLp, an
R will affect the A-pos or C-pos of formulas in its scope just as if it
were an 'N'.
We may now begin our comparison of Gamma-MR with an "ordinary" modal logic. The calculus used here will be the Ł-modal system. In our comparison of alpha with the CPC we found it convenient to use two formulations of that calculus, Pr and Pw, the former with "K-N" primitive, the latter with "C-
Æ" primitive. We may similarly think of two formulations of Ł-modal, one with "K-N-R" primitive ('R', of course, being our possibly-not operator) and the other with "C-Æ-R" as primitive. In chapter I we defined functions f, h, and g; it should be evident that we may extend these functions so that they may be able to relate the broken cut systems to systems like L-modal. All that is required here is an instruction to correlate the broken cut to the modal operator 'R'. Call the functions thus extended f*, h*, and g*, respectively.In chapterI, we showed that f of the single axiom of alpha, the null-graph, is a theorem of Pr. The null-graph b is also the only axiom of Gamma-MR; f*(b) is '
~(p0 . ~p0)' , just as was f(b). Clearly, then, f*(b) is a theorem of Ł-modal.We also showed in chapter I that when R(Y, X) is one of the rules of inference of alpha, and is true for alpha graphs X and Y, then if f(X) is a CPC theorem, so too is f(Y).
The rules of inference of alpha hold unrestricted in Gamma-MR But *3.01 and *3.02 hold for Ł-modal, and the schema
![]() CdpCdNpdq
CdpCdNpdq![]()
holds unrestricted in Ł-modal, as we have mentioned (it is, in fact, an axiom-schema of that system). There would then be no trouble in extending the proof s of chapter I to show that when R(Y, X) is one of the alpha rules as employed in Gamma-MR, and is true for Gamma-MR graphs X and Y, then if f*(X) is a theorem of Ł-modal, then so too is f*(Y).
Gamma-MR also includes two rules for the broken cut -- Rgam, which permits an evenly enclosed alpha cut to be transformed to a broken cut, and Rngm, which permits an oddly enclosed broken cut to be transformed to an alpha cut. Ł-modal, of course, contains the law 'CNpRp'; in the presence of *3.01 and *3.02, this means -- since the broken cut is correlated by our functions to 'R' just as the alpha cut is to 'N' -- that if either Rgam(Y, X ) or Rngm(Y, X) is true for Gamma-MR graphs X and Y, then if f*(X) is an Ł-modal theorem, so too is f*(Y).
In summary, all of the above means that
If X is a theorem of Gamma-MR, then f*(X) is a theorem of Ł-modal.
Now turning to the "other direction" of the proof, recall again that the rules of insertion and erasure, iteration and deiteration, and positive and negative biclosure hold unrestricted in Gamma-MR. This means that the graph
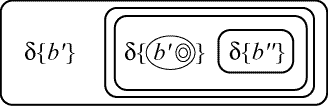
is provable in Gamma-MR just as it is in alpha, even though here '
d{ }' may stand for any graphical context, may include broken cuts. This graph corresponds by g* (or by h*) to the axiom-schema of Ł-modal, which is "unrestricted" in the same sense as is this "graph-schema.''The graph
is trivially provable in Gamma-MR by Rgam and the alpha rules. This graph corresponds by g* (or by h*) to the Ł-modal axiom 'CNpRp' (which is, of course, equivalent to 'CLpp').
It is clear that the analogs of the rules of substitution and detachment hold in Gamma-MR as "derived rules of. inference" just as they do in alpha.
Given the above, we submit that the following hold, as analogs of *1.17 and *1.21 of chapter I:
If f*(X) is a theorem of Ł-modal, then X is a theorem of Gamma-MR
and
A is a theorem of Ł-modal iff g*(X) is a theorem of Gamma-MR.
The three indented, color-marked statements in the above development assert equivalently that Ł-modal and Gamma-MR are translatable into each other in our technical sense of "translatable." And they mean that Gamma-MR and Ł-modal are equivalent to each other in the same sense that alpha is equivalent to the CPC. This result should not have been unexpected, since the unrestricted ''cross-breeding" of alpha and gamma concepts in Gamma-MR is strikingly like the unrestricted "cross-breeding" of truth functional and modal concepts in the Ł-modal system.
To drive the point home a little harder, we shall now engage in a few graphical derivations within Gamma-MR. We shall prove within Gamma-MR some typical graphs of the system; they shall be seen to correspond to characteristic theses of the Ł-modal system.
By alpha rules
|
|
(1) | |
| (1), Ritr, Rbcl |
.gif) |
(2) |
| (2), Ritr (note the dependence on unrestricted Ritr) |
.gif) |
(3) |
| (3), Rbcl |
.gif) |
(4) |
Note that given the definitions 'L' for 'NR' and 'Np' for 'CpÆ' , (4) is equivalent to a characteristic Ł-modal thesis, 'CLCpqCpLq'. The critical step of this deduction is (3), where b
¢ is iterated across a broken cut, as permitted by the rules of Gamma-MR. We shall see that in the other broken cut systems we shall examine, this move, and so the graph of (4), is forbidden. We now go on to the proof of a graph which, while not peculiar to Gamma-MR, may prove a bit surprising.| alpha rules |
|
(5) |
| alpha rules |
.gif) |
(6) |
| (6), Rbcl |
.gif) |
(7) |
| (7), Rgam |
.gif) |
(8) |
| (8), Ritr |
.gif) |
(9) |
| (9), Rdit |
.gif) |
(10) |
| (10), (5). Rdit |
.gif) |
(11) |
| (11), Rnbc |
.gif) |
(12) |
The graphs at (11) and (12) express, equivalently, the thesis 'RR1' [equivalent to RRCpp] or 'ML1' ; they assert that the "true" is "possibly necessary." The thing one might find surprising is that the simple "broken cut biclosure" with a broken cut enclosed oddly is a thesis of Gamma-MR, derivable only by the rules. It is not immediately apparent from an examination of Rgam, for example, that this is possible. Yet this theorem should not be too surprising considering that Gamma-MR and Ł-modal are equivalent to each other, and 'ML1' is a law of Ł-modal.
We set about the proof, now, of one more characteristic graph of Gamma-MR, again, one that is equivalent to a characteristic thesis of Ł-modal.
| (12), Rbcl, Rins |
.gif) |
(13) |
| (13), Ritr |
.gif) |
(14) |
| alpha rules |
.gif) |
(15) |
| (15), Ritr, Rins |
.gif) |
(16) |
| (16), Rbcl. Ritr |
.gif) |
(17) |
| (17), Rngm, Rnbc |
.gif) |
(18) |
| (18), Rnbc |
.gif) |
(19) |
The graph at (19) is a typical Gamma-MR graph, equivalent to
the Ł-modal 'CCpqCMpMq'; now take b¢¢
as :
![]()
.gif) |
(20) | |
| (14), (20), Rdit |
.gif) |
(21) |
| alpha rules |
.gif) |
(22) |
| (22), Rins |
.gif) |
(23) |
| (23), Ritr |
.gif) |
(24) |
| alpha rules |
.gif) |
(25) |
| Now in (25), take b¢ as: |
|
b¢¢ as: |
.gif) |
b¢¢¢ as |
|
Then, with (25) (with these substitutions), (21), (24), Rdit, and Rnbc, we have:
.gif) |
(26) |
The graph of (26) says the same thing as the formula 'CMpMLp'; it is thus a "map" of a characteristic Ł-modal thesis. Note that step (16) in the above deduction, for example, again employs the unrestricted "iteration across broken cuts" characteristic of Gamma-MR.
The system Gamma-MR yields unusual modal graphs, just as Ł-modal gives us unusual modal formulas. In both case the root of the strangeness is the "extensionalizing" of modal concepts. In Ł-modal this is accomplished by permitting unlimited or unrestricted use of modal contexts in schemata like CdpCdNpdq'; this schema is often referred to as the "thesis of extensionality" (actually, it is but one of several schemata to which the name is appropriate). In the "classical" Lewis-modal systems, of course, such unrestricted treatment of modal operators is not permitted; the closest we can come to a thesis of extensionality in these systems is
CLCpqCLCqpCdpdq (n1)
which is a statement of the substitutivity of strict equivalence, a principle which, as a rule of inference, is characteristic of all the Lewis modal systems, and which is considerably weaker than the Ł-modal theses of extensionality.
In Gamma-MR, the "extensionalizing" is accomplished by the unrestricted permission to use the rules Ritr and Rdit. The theses *3.01 and *3.02 show that the rules of insertion and erasure hold unrestricted even for gamma systems which might be called "Lewis-type," as we shall see; the rules of biclosure and for the broken cut also hold without restriction. The strange nature of Gamma-MR may then be credited to its unrestricted rules of iteration and deiteration.
Another remark is in order here: in 4.518 Peirce
indicates that if a graph X is assertable at one "state of information,"
then ![]() will be assertable at succeeding states of information. This is much
like the move in some Lewis-modal systems justified by RL: "If
a is a theorem,
then
will be assertable at succeeding states of information. This is much
like the move in some Lewis-modal systems justified by RL: "If
a is a theorem,
then ![]() La
La![]() is a theorem." It is perhaps needless to say that this move cannot be permitted
in Gamma-MR. Such a permission, in the presence of the theorems of
Gamma-MR. would result in the collapsing of the modal structure of the system,
just as the theoremhood of 'LCpp' would do for Ł-modal. The relationship of
gamma-MR and Ł-modal, in fact, bars all graphs of form
is a theorem." It is perhaps needless to say that this move cannot be permitted
in Gamma-MR. Such a permission, in the presence of the theorems of
Gamma-MR. would result in the collapsing of the modal structure of the system,
just as the theoremhood of 'LCpp' would do for Ł-modal. The relationship of
gamma-MR and Ł-modal, in fact, bars all graphs of form
![]() from theoremhood in
Gamma-MR, since all formulas of form
from theoremhood in
Gamma-MR, since all formulas of form
![]() La
La![]() are rejected in Ł-modal.
are rejected in Ł-modal.
3.22 Gamma-4: A "Classical" Broken Cut System
There is little subtlety to the name we have chosen to give the broken cut
system of the present section; it is a system which bears the same relation to
the Lewis-modal S4 that Gamma-MR bears to the Ł-modal system. As we have
indicated, the statement of rules for Gamma-4 will involve a restriction on the
application of the rules Ritr and Rdit. It will also involve the axiomatic
assertion of a certain extra graph. Although the graph
![]() was derivable as a theorem of
Gamma-MR, the graph
was derivable as a theorem of
Gamma-MR, the graph
![]() was not derivable there, as indicated by the relationship between
Gamma-MR and Ł-modal. This latter graph, we might say; asserts "the necessity
of the true." But in all the Lewis-modal systems, there is a sense in which the
true is necessary; even in the very weakest systems, like
Lemmon' s S0.5,(n1) there are rules
which permit us to move from the theoremhood of a formula
a (belonging to a
certain set of theorems, depending on the system) to the theoremhood of
was not derivable there, as indicated by the relationship between
Gamma-MR and Ł-modal. This latter graph, we might say; asserts "the necessity
of the true." But in all the Lewis-modal systems, there is a sense in which the
true is necessary; even in the very weakest systems, like
Lemmon' s S0.5,(n1) there are rules
which permit us to move from the theoremhood of a formula
a (belonging to a
certain set of theorems, depending on the system) to the theoremhood of
![]() La
La![]() .
In S0.5, this rule is simply, "If
a is tautologous,
.
In S0.5, this rule is simply, "If
a is tautologous,
![]() La
La![]() is a theorem"; but in the systems from T through S5, the presence
of the unrestricted rule RL permits us to move from the assertion of any
theorem to the assertion of the necessity of that theorem. In Gamma-4 we
shall discover that we can get the same results with the simple axiomatic
assertion of the graph
is a theorem"; but in the systems from T through S5, the presence
of the unrestricted rule RL permits us to move from the assertion of any
theorem to the assertion of the necessity of that theorem. In Gamma-4 we
shall discover that we can get the same results with the simple axiomatic
assertion of the graph
![]()
which is what we might call 'the necessity biclosure." Needless to say, the presence of this graph does not give us the right to use this pair of cuts as if it were a pair of alpha cuts in the application of the rules Rbcl and Rnbc. These rules will still apply just to the insertion or deletion of alpha biclosures. Note too that with Rngm and Rnbc there is no trouble in getting from this graph as axiom to the null graph b as theorem.
We shall now state the axiom and the rules as they apply to Gamma-4, just as we did for Gamma-MR.
The sole axiom of Gamma-4 is the graph
Rules Rins and Rers apply just as they did in Gamma-MR, again counting alpha and broken cuts alike to determine oddness or evenness of enclosure.
The rules Ritr and Rdit will apply as before, except for the following restriction: The only graphs that may be iterated or deiterated across broken cuts are those of form
The rules Rbcl and Rnbc apply as in Gamma-MR.
The rules Rgam and Rngm (for the broken cut) apply as in Gamma-MR.
The restriction on the rules of iteration and deiteration prevents an iteration in Gamma-4 like that leading from step (2) to step (3) in the deductions of Section 3.21.
We turn our attention to the status of these rules in the system S4. First of all, the strict implication
LCNpRp
is a thesis of S4. By *3.01 and *3.02, this indicates
that any subformula beginning with 'N' and standing in a C-pos in an
S4 theorem -- that is, a subformula
![]() Na
Na![]() -- may be replaced by the same formula with an 'R' in place of the 'N'
-- that is, by the subformula
-- may be replaced by the same formula with an 'R' in place of the 'N'
-- that is, by the subformula
![]() Ra
Ra![]() . And also, any subformula
. And also, any subformula
![]() Ra
Ra![]() standing in an A-pos in a law of S4 may be replaced by
standing in an A-pos in a law of S4 may be replaced by
![]() Na
Na![]() .
.
This indicates that whenever, for Gamma-4 graphs X and Y, either Rgam(Y, X) or Rngm(Y, X) is true, then if f*(X) is ari S4 theorem, then so too is f*(Y) .
The strict implication
LCKpqp
is also a law of S4; in the presence of *3.01 and *3.02 this means that the rules of insertion in odd and erasure in even have analogous derived rules of inference in S4, just as do the above mentioned rules for the broken cut.
A strict equivalence that holds in S4 is
LEpNNp.
Since the system S4 contains the rule of substitutivity of strict equivalence, this means that the rules of biclosure have analogous derived rules of inference in S4.
We move now to the rules of iteration and deiteration as stated for Gamma-4. It will be recalled that the proof in chapter I that the CPC contains rules analogous to Ritr and Rdit pivots about the existence in CPC of a certain theorem schema which for our purposes here we may express as:
| EKpd1Kpdp | (1) |
If this schema is in a system, and the system contains the rule of substitutivity of material equivalence, then that system contains derived rules of inference analogous to Ritr and Rdit. The schema at (1) quite definitely does not hold in the general case in S4; however, recalling the nature of the restriction on the rules of iteration and deiteration in Gamma-4, it is possible t o write a schema which does hold in S4 and whose presence makes possible proofs of the versions of iteration and deiteration appropriate to S4.
A little thought will tell us what this schema must be; we will recall that
the restriction on iteration and deiteration for Gamma-4 states that only
graphs of form ![]() may be iterated across broken cuts, that is, iterated "into modal contexts."
This suggests that the schema we want in the general case in S4 is:
may be iterated across broken cuts, that is, iterated "into modal contexts."
This suggests that the schema we want in the general case in S4 is:
| LEKLpd1KLpdLp | (2) |
Actually, the simple
| EKLpd1KLpdLp | (3) |
will do, since we can always move from (3) to (2) by RL. The existence of (2) and the substitutivity of strict equivalence in S4 would permit us to say that in the general case, where 'd' may be a modal context, analogs of the rules of iteration and deiteration of Gamma-4 exist in S4.
It will be noted that when 'd' is a non-modal context, that is, when the schema is to parallel iterations across alpha cuts only,
EKpd1Kpdp
does hold in S4 just as it does in CPC.
We shall now show that (3) is indeed a theorem schema in the general case in S4. The following schema holds in S4:(n1)
| CLCpqCLqpCdqdp | (4), |
where 'd' may represent any S4 context at all.
| By (4). q / 1 | CLCp1CL1pCd1dp | (5) |
| (5), LCp1, PC | CLC1pCd1dp | (6) |
The following is an easily provable S4 thesis
| CLpLCqp | (7) | |
| (6). (7). PC | CLpCd1dp | (8) |
| (8), p / Lp | CLLpCd1dp | (9) |
But 'LELLpLp' is a theorem of S4; by (9) and substitutivity of strict equivalence, then:
| CLpCd1dLp | (10) | |
| (10), PC | CKLpd1KLpdLp | (11) |
But (11) is one half of (3), which is the formula we wished to prove. The converse of (11) is provable along much the same lines that (11) was. We may then say that (3) holds in the general case in S4. But this means that when, for Gamma-4 graphs X and Y, Ritr(Y, X) or Rdit(Y, X) is true with the Gamma-4 restriction, then if f*(X) is an S4 theorem, so too is f*(Y).
Now we note that where X is the sole axiom of Gamma-4, then f*(X) is 'NRNKp0Np0', which is the same as 'LCp0p0' , and is clearly a theorem of S4. We may say, then, that:
If X is a theorem of Gamma-4, f*(X) is a theorem of S4.
We shall now go on to show both that the converse of the above statement holds, and that the set of theorems of S4 maps into the set of theorems of Gamma-4 by the function g*: (f* and g*, we should recall, are the functions f and g of chapter I extended to account for the broken cut). Gamma-4 contains all that alpha contains and more. We shall have accomplished our purpose, then, if we can show that the axioms and rule of S4 beyond those of the CPC map appropriately into the set of theorems of Gamma-4. First of all, we may easily prove the following:
| alpha rules |
.gif) |
(12) |
| (12), Rgam |
.gif) |
(13) |
The graph at (13) is clearly a correlate by g* or h* of our axiom 2 for S4, 'CNpRp'. Now:
| Gamma-4 axiom, Rbcl |
.gif) |
(14) |
| (14), Rins |
.gif) |
(15) |
| (15), Ritr |
.gif) |
(16) |
| (16), Rbcl |
.gif) |
(17) |
| (17), Ritr |
.gif) |
(18) |
| (18), Rngm |
.gif) |
(19) |
| (19), Rbcl, Rnbc |
.gif) |
(20) |
Now in (20), take
![]() as
as
![]() and
and ![]() as
as ![]() ; the
graph resulting from these substitutions contains a "replica"
of (20) itself. Deiterate this "replica" with (20) and apply Rnbc
and Rngm to obtain
; the
graph resulting from these substitutions contains a "replica"
of (20) itself. Deiterate this "replica" with (20) and apply Rnbc
and Rngm to obtain
.gif) |
(21) | |
| by alpha rules |
.gif) |
(22) |
| (22), Rins |
.gif) |
(23) |
| (23), Ritr |
.gif) |
(24) |
We may now move, by purely alpha methods, employing (21), (24), and the alpha-provable graph [this is like transitivity of implication in PC]
.gif) |
(25) |
to
.gif) |
(26) |
The graph at (26) will be found, upon examination, to correspond to our axiom 1¢ for S4, 'CRCRpRqCpq'. The graph of (24) corresponds to 'CRNRpRp', which becomes, on transposition of antecedent and consequent, 'CLpLLp', the characteristic reduction formula of S4.
Note that with
![]() as an axiom
of Gamma-4, the equivalent of RL holds in Gamma-4. This is
so because any graph derivable as a theorem upon the blank SA alone will be
derivable as a theorem within the "necessity biclosure" which is the Gamma-4
axiom; this point is illustrated by the deduction leading
to the graph of (20) above. It is now fairly clear that both:
as an axiom
of Gamma-4, the equivalent of RL holds in Gamma-4. This is
so because any graph derivable as a theorem upon the blank SA alone will be
derivable as a theorem within the "necessity biclosure" which is the Gamma-4
axiom; this point is illustrated by the deduction leading
to the graph of (20) above. It is now fairly clear that both:
A is s a theorem of S4 iff g*(A) is a theorem of Gamma-4,
and
If f*(X) is a theorem of S4, then X is a theorem of Gamma-4.
The latter by an extension of the argument leading to the proof of its analog in chapter I.
Gamma-4 is then a graphical version of the Lewis modal S4. One might suspect that there are other Lewis modal systems which may be formulated in the broken cut notation; this in fact is the case.
3.23 Gamma-4.2: Another "Lewis-Modal" Broken Cut System
Situated between the Lewis-modal systems S4 and S5 are at least two other systems. They are situated between these systems in the sense that their sets of theorems include those of S4 and are included in those of S5. These systems may be formulated by subjoining to S4 certain additional axioms. One of these systems, S4.2, is formed by adding to S4 the axiom
CMLpLMp.
The other, S4.3, is formed by adding to S4 the axiom
ALCLpgLCLqp.
S4.2 is contained in S4.3, We shall here sat down a broken cut system, Gamma-4.2, which bears the same relation to S4,2 that Gamma-4 bears to S4.
The system Gamma-4.2 is based upon Gamma-4. It is just the same
as Gamma-4 except for a slightly more liberal restriction attached to the
rules Ritr and Rdit. Gamma-4
permitted graphs of form
![]() to be iterated
and deiterated through broken cuts; Gamma-4.2 will
permit as well graphs of form
to be iterated
and deiterated through broken cuts; Gamma-4.2 will
permit as well graphs of form
![]() to be so
iterated. Otherwise the systems are the same.
to be so
iterated. Otherwise the systems are the same.
All that we have said about Gamma-4 and S4, then, applies to Gamma-4.2 and S4.2; we have in addition, however, to prove the rules of iteration and deiteration with the new restriction in S4.2, and to prove a graph in Gamma-4.2 corresponding to the special axiom of S4.2.
Recall how we went about the proof of the rules of iteration and deiteration in S4. Whether or not these rules held there was a function of whether or not the schema
EKLpd1KLpdLp
held in S4. The above schema holds in S4.2, to be sure, as well as in S4. But we must show something more for S4.2; the restriction on the rules of iteration and deiteration has been relaxed in this system to permit graphs enclosed by two broken cuts to be iterated or deiterated through broken cuts. The pair of broken cuts is correlated by our translation functions to the modal prefix 'RR', which is equivalent to 'ML'. This suggests that the additional schema which we must show to exist in S4.2 is
EKMLpd1KMLpdMLp
A little reflection will show us that this is indeed the case. Let us turn to step (8) in the deductions of the preceding section, and instead of substituting Lp for p, substitute MLp (we begin the numbering anew in this section):
| CLMLpCd1dMLp | (1) |
Now, in S4.2 the following thesis holds -- it is not a law of S4:
| CMLpLMLp | (2) | |
| (1), (2), PC | CMLpCd1dMLp | (3) |
| (3), PC | CKMLpd1KMLpdMLp | (4) |
We noted that the converse of the analogous formula in Section 3.22 is proven much as is that formula itself; so too will the converse of (4) follow, and we may state that
| EKMLpd1KMLpdMLp | (5). |
The formula at (5) is the one we wanted, and we are safe in saying that appropriate analogs of the rules of iteration and deiteration with their Gamma-4.2 restrictions hold in S4.2. Since all else in Gamma-4.2 is as in Gamma-4, we may conclude that
A graph X is a theorem of Gamma-4.2 only if f*(X) is a theorem of S4.2.
To show that the converse of the above holds, and also that the set of S4.2 theorems maps into the set of Garmna-4.2 theorems by g*, we must show only that there is a theorem of Gamma-4.2 which corresponds by g* and h* to the special axiom of S4.2, 'CMLpLMp' -- or, in 'R', 'CRRpNRRNp'.
| Gamma-4 axiom |
|
(6) |
| (6), Rins |
.gif) |
(7) |
| (6), Ritr, (in Gamma-4.2 version) |
.gif) |
(8) |
| (8), Rngm |
.gif) |
(9) |
| (8), Rbcl |
.gif) |
(10) |
The graph of (10) states 'CRRpNRRNp', which is the same as 'CMLpLMp', Note the characteristic Gamma-4.2 operation at step (8). It is now safe for us to state, on the basis of the above, our work in Section 3.22, and the relationship between S4 and S4.2, that both:
If f*(X) is an S4.2 theorem, then X is a theorem of Gamma-4.2,
and
A is a theorem of S4.2 iff g*(A) is a theorem of Gamma-4-.2.
The systems S4.2 and Gamma-4.2 are then translatable into each other, and also may be considered equivalent in the same sense that alpha is equivalent to the CPC,
3.24 Gamma-5: The Limiting "Lewis-Modal" Broken Cut System
In many respects, the system S5 may be considered a "limiting" system among the Lewis-modal calculi -- to go into an e extensive study of this, however, would really be outside the scope of this paper.(n1)
The system Gamma-5 is to be a "broken-cut" version of S5; this is why we have called it a "limiting" broken cut system. As might be suspected, Gamma-5 differs from Gamma-4 and Gamma-4.2 only in having a different, more lenient restriction upon its application of the rules of iteration and deiteration. The statement of this restriction is quite simple:
In Gamma-5, the rules Ritr and Rdit apply as they do in alpha, except that a graph X may be iterated or deiterated across a broken cut only if each of X's minimal graphs is in the "scope" of a broken cut belonging to X, that is, provided each of the minimal graphs of X is part of a subgraph of X whose "outermost sign" is a broken cut.
As was the case in Sections 3.22 and 3.23, we shall state a formula whose theoremhood in S5 will guarantee the existence in S5 of derived rules of inference analogous to the rules of iteration and deiteration with the above restriction. The formula is
| where a is any formula of S5 having each of its propositional variables in the scope of a modal operator belonging to a: | EKad1Kada | (1) |
All the theorems of S4 and S4.2, of course, hold in S5; the schema at (1) is one which does not hold in general in S4 and S4.2, but which will be shown to hold in S5. As was the case in Section 3.23, we shall first turn to step (8) in the deductions of Section 3.22, and now, instead of substituting ' Lp' for 'p', we shall substitute
a, where a is any wff having each of its propositional variables in the scope of a modal operator belonging to a . The result is| CLaCd1da | (2) |
Now, there is a pair of rules of inference, due to Prior, which hold in S5 and which -- when subjoined to the CPC -- actually form a basis sufficient for S5.(n1) The rules are:
| R1: | If
|
| R2: | If
|
We have, by PC alone:
| Caa | (3) |
But let
a be of such a form that each of its propositional variables is part of a subformula of a beginning with a modal operator; this means both that the proviso of R2 is fulfilled and that a is the same as the a of the schema at (2). Then:| (3), R2 | CaLa | (4) |
| (2), (4 ), PC | CaCd1da | (5) |
| (5), PC | CKad1Kada | (6) |
Again, the converse of (6) will be easily provable, and we may state:
| EKad1Kada | (7) |
where a, of course, is as required in (1).
But (7) is the schema we needed, and so, in the light of all that has gone before, we may state
If X is a theorem of Gamma-5, then f*(X) is a theorem of S5.
To show that the converse of the above holds and that the set of S5 theorems maps into the set of Gamma-5 theorems by it would be sufficient to show that a graphical correlate of our axiom 1¢¢ is a theorem of Gamma-5; 1¢¢ is, of course, 'CRRCpqCRqRp'. But actually it will not be necessary to develop a proof for this particular graph. We know that if the formula 'CMLpLp' is added to a base sufficient for S4, the result is the system S5, Another formula which will do the job, and which, in fact, is just a transposed version of 'CMLpLp' is
CNLpLNLp.
Another way of writing this formula is
CRpNRRp.
Since Gamma-5, with a more liberal restriction on its rules of iteration and deiteration than either of the other such systems we have discussed, will contain all the theorems of both of these systems, it is clear that if a graph corresponding to the last mentioned axiom can be proven in Gamma-5, then graphs corresponding to all S5 theses will be derivable. The proof is as follows:
| Gamma-4 axiom |
|
(8) |
| (8), Rins |
.gif) |
(9) |
| (9), Ritr, (Gamma-5 version) |
.gif) |
(10) |
| (10), Rbcl |
.gif) |
(11) |
The graph of (11), a theorem of Gamma-5, corresponds by g* or h* to 'CRpNRRp', We are then safe in asserting that both:
If f*(X) is an S5 theorem, then X is a theorem of Gamma-5,
and
A is a theorem of S5 iff g*(A) is a theorem of Gamma-5.
The systems S5 and Gamma-5 are then translatable into each other, in our technical sense of translatable; and we may consider them equivalent in the same sense that alpha and the CPC are equivalent.
3.25 A Summary of the Broken Cut Systems Here Presented
In the preceding sections we have shown how systems equivalent to some contemporary modal systems may be formulated within the "broken cut" notation of Peirce's gamma graphs. The method of setting up these systems is quite simple. We add to the notation and rules of alpha the broken cut and the rules which permit us to change an evenly enclosed or unenclosed alpha cut into a broken cut, and an oddly enclosed broken cut into an alpha cut. We allow the rules of insertion in odd and erasure in even and of biclosure to hold just as they do in alpha, counting broken cuts as if they were alpha cuts to determine whether an enclosure is odd or even. If we add no new graphical axiom and allow the rules of iteration and deiteration to apply with no restrictions, the system obtained, Gamma-MR, is equivalent to Ł-modal.
If we add as an axiom the graph
![]() and place
certain restrictions on the rules of iteration and deiteration, we shall obtain
several different systems, depending on what the restrictions are.
and place
certain restrictions on the rules of iteration and deiteration, we shall obtain
several different systems, depending on what the restrictions are.
If we state that only graphs of form
![]() may be
iterated or reiterated through broken cuts, we get the system Gamma-4,
which is equivalent to the Lewis-modal S4.
may be
iterated or reiterated through broken cuts, we get the system Gamma-4,
which is equivalent to the Lewis-modal S4.
If we permit also graphs of form
![]() to be iterated
or deiterated through broken cuts, the system yielded is Gamma-4.2, which
is equivalent to the Lewis-modal S4.2.
to be iterated
or deiterated through broken cuts, the system yielded is Gamma-4.2, which
is equivalent to the Lewis-modal S4.2.
If we permit any graph all of whose minimal graphs are within the scope of broken cuts belonging to that graph to be so iterated or deiterated, we get Gamma-5, which is equivalent to the system S5.
It is not by accident that the Lewis-modal broken cut systems are so formulable. In an article on these systems(n1) I have shown that S4 and S4.2 may be formulated by the subjunction of Prior' s rules R1 and R2 (which we saw in Section 3.24) to the CPC, changing the proviso of R2 to read, "Provided a is completely modalized." I distinguish between S4, S4.2, and S5 by stating for each of these systems what it is to be completely modalized. In S4 we find that a formula is completely modalized if it begins with an 'L' or is a conjunction of formulas each of which begins with an 'L'. In S4.2 we find that in addition formulas beginning with 'ML' will be completely modalized. For S5, complete modalization is as in Prior's version of the proviso.
It is interesting to note that these definitions of "complete modalization" correspond to the restrictions on iteration and deiteration for the respective systems Gamma-4, Gamma-4.2, and Gamma-5. We might, then, state the restriction on these rules in another way, and specify that for all three of these systems iteration or deiteration through a broken cut is pemitted only for a "completely modalized graph" -- this would be a thread connecting these three gamma-systems. We would then identify each of these systems by a specification of what it is in that system for a graph to be completely modalized.
It is not at all impossible that other Lewis-modal systems might be formulated as broken cut systems -- at least I know of no reason why it should be impossible. At the moment, however, we shall go no further in this direction. We will remark, however, that the formulability of these broken cut systems in really so simple a manner is another tribute to the power of the graphs and to the ingenuity of the man who first thought of them.
3.3 Cleaning Up
It is sad to note, perhaps, that from certain points of view the Existential Graphs, into which Peirce poured so much effort, are a failure. The final formulation of the gamma graphs as he envisaged it did not come off, and indeed, seems to have been doomed from the start. From this failure follows the failure of the graphs as the ultimate analytical instrument of deductive reasoning in the broadest sense. And this makes the graphs, from this point of view, just an unfinished wing in the uncompleted structure that was the philosophy of C. S. Peirce. But the graphs need not be viewed only from this point of view. As logical systems they are astoundingly successful. They seem somewhat awkward to work with, especially till you get the hang of them, but so too are many contemporary systems, when considered in their primitive notation. The graphs are, as we have seen, systems of considerable power, both in the theorems derivable within them, and in the insights they afford into logic in general.
Much remains to be done with the graphs. We have offered a sketch, in the Introduction, of how we feel the graphs fit into Peirce' s philosophy as a whole; this sketch could be expanded into an interesting study of considerable length, I am sure. Much might also be said about the place of the graphs in Peirce' s theory of signs. There are also intriguing little suggestions by Peirce regarding formal features of the graphs, such as the "state of information LI" which he mentions in 4.251 -- here we might find matter for further study and expansion, as we have studied and expanded the broken cut systems.
This paper has studied the more important parts of the graphs, those about which Peirce told us the most; it has studied them as logics. And from the point of view which this paper has adopted, we can only say that the graphs are not a failure at all, but a grand success.