
A CASUAL thumbing through Volumes III and IV of the Collected Papers of C. S. Peirce will turn up a fair number of kinds of diagrams each of which has some claim to the title "Logical Diagram" or "Logical Graph" In this paper I shall examine in detail one family of these diagrams -- or better, of systems of these diagrams -- to which the name "Graphical Logic" may fairly be applied. These systems are the systems of "Existential Graphs," and the principal material on them is located in Volume IV of the Collected Papers, in paragraphs 372 to 584.
Peirce developed these systems about the turn of the century -- Murray Murphey gives the year as 1896.(n1) Peirce called the graphs his "chef d'oeuvre,"(n2) but for the chef d'oeuvre of one of the great logicians, they have received scant attention till now. The present work aims at a thorough study of the existential graphs, using the methods of contemporary logic, I shall attempt to determine what the existential graphs are as systems, and how certain of these systems may be fruitfully extended in the light of modern formal logic.
Although the primary aim of this paper is a study of the graphs as formal. systems, I shall also devote some space in this introduction to a brief investigation of the graphs as part of Peirce's philosophy; I shall here present my view on why Peirce considered the existential graphs to be his most important work.
By 1885 Peirce had developed his "algebra of logic" into a fairly rich system or group of systems (3.359 ff.). He had definite ideas as to the raison d'etre of a system of symbolic logic; the purpose of such a system is "simply and solely the investigation of the theory of logic, and not at all the construction of a calculus to aid the drawing, of inferences" (4.3?3). Some comment on Peirce's use of the word calculus in in order here, It is fairly clear that he was thinking of a calculus as a "computing aid" of some kind, possibly a system to be used as logarithms, for instance, frequently are. Peirce saw "calculi" as systems which would reduce to a minimum the number of steps in a deduction from premises to a conclusion. A logic, on the other hand, would be a system which would break down the steps in the deduction to the smallest possible units and thereby exhibit the deductive process involved. For Peirce, then, a calculus is a tool for turning out answers to specific problems, while a logic is a tool for investigating the deductive process itself. (We have taken time to distinguish between Peirce's use of these terms since "logic" is often taken to mean the same as "calculus" in contemporary literature on logic.)
Referring to the investigation of the deductive process, Peirce states, "This, then, is the purpose for which my logical algebras were designed" (4.429). But he adds, "In my opinion, they do not sufficiently fulfill" this purpose (4.429).
"This purpose," Peirce felt, was better fulfilled by the systems of existential graphs than by the algebra of logic We shall examine in some detail the reasons why Peirce felt this way; first, however, we shall see what the existential graphs are, We shall familiarize ourselves with the symbols of these systems and with! the rules that govern these systems; this will be a helpful -- or even necessary -- prologue both to our examination of the graphs as Peirce now them and to our rigorous formal study of the graphs as logical systems, which will commence in chapter I.
Symbols of the Existential Graphs
Before we consider the graphs as part of Peirce's philosophy or enter into a rigorous formal study of these systems, , we shall introduce ourselves to the terminology and deductive method of the graphs, and we shall note some strands which connect the various systems.
First of all, Peirce defines "graph" as "the propositional expression in the System of Existential Graphs of any possible state of the universe" (4.359). The existential graphs are then intended by Peirce to be systems of "propositions" or "assertions."
Peirce presents the graphs as three general systems called, respectively, "alpha," "beta," and "gamma." This division corresponds fairly well to his division of the "algebra of logic" into "non-relative logic," "first-intentional logic of relations," and "second-intentional logic of relations" (3.359 ff. ), The first and possibly most important sign of the graphical systems -- one common to all three of them -- is the "sheet of assertion" (far which we shall often use the abbreviation "SA" ). SA is a surface upon which the graphs are to be "scribed" according to the "rules of transformation" of the systems. SA itself, even before any of these rules has been applied to it, is to be considered a graph (4.396). Also, according to Peirce, the SA is to be taken as "representing the universe of discourse, and as asserting whatever is taken for granted . . . to be true of that universe" (4.396). The SA in its "initial state" (before any of the rules we shall subsequently state has been applied to it), then, may be considered to represent a kind of "postulate set" to be operated upon by appropriate rules, The content of the "postulates" will depend upon what we wish to "reason about" with the graphs We might Imagine a sheet of assertion, for example, being set up initially to "deductively reason about" one of those cute little problems we find in the Lewis Carroll logic books. In this case we would consider the special "extralogical" premises or postulates needed for the problem at hand to be part of the initial SA. For the purpose of this paper, that of examining the graphs as formal systems, we shall find that very little is the way of such postulates or premises is needed. For alpha, as an example, all we will need to begin with is a completely blank SA.
Among the signs which may, under appropriate circumstances, be scribed upon SA is one common to all three general graph systems. In some places (as in 4.399) Peirce calls this sign a "cut";
 |
| The Alpha Cut |
in others (as in 4.435) he refers to it as a "sep" -- from the Latin saepes, "fence." The "alpha cut," which we will ordinarily refer to simply as the "cut," except when there is danger of confusion, is defined by Peirce as "a self-returning linear separation (naturally represented by a finely drawn or peculiarly colored line) which severs all that it encloses from the sheet of assertion on which is stands itself, or from any other area on which it stands itself" (4.399). The cut "cuts off" what it encloses from the area on which it stands. If a graph is an assertion, a sentence, then the enclosure of that graph by a cut is, in effect, an assertion that the enclosed graph Is not asserted. The cut, then, may be considered a negation sign, inasmuch as it cuts something off from the asserted universe of discourse represented by SA. We shall find, indeed, that the alpha cut is completely analogous to the ordinary negation sign of the propositional calculus. And if two or more graphs occur in the same area, with no cuts between then, they may be considered to be asserted simultaneously in. that area; such "unseparated occurrence" of graphs is analogous to PC conjunction.
Peirce mentions in passing other kinds of cuts than the one referred to above. The one of these other cuts to which he gives a significant amount of attention is one belonging to the gamma part of the graphs; it may be called the "broken cut."
 |
 |
 |
| The Broken Cut | The Scroll: Two Versions | |
As the name implies, it consists of a broken rather than a continuous line {4.516) and may be interpreted as asserting "possibly not" of its contents; a system containing the broken cut among its signs may therefore be considered a modal system.
In 4.436 and 4.437 we find Peirce referring to what we sight want to consider a superfluous sign, and referring to it in in language which indicates that he thought of it as a primitive kind of sign. The sign is the "scroll," which consists of two cuts, one enclosing; the other, whether they are connected by a node or not, Although the scroll is merely two cuts, and although we shall seldom refer to it by name, we shall find that the notion of the scroll -- that is, of two cuts acting as a unit -- does play a fairly important part at certain phases of our detailed discussion of alpha in chapter I.
Next we shall consider signs characteristic of each of the systems. The alpha system might be considered a set of graphical manipulations of "unanalysed" statements; that is, the "minimal unit" of alpha is a graph representing a complete, closed sentence. Alpha does not contain the apparatus for expressing or analysing the components of its minimal or atomic sentences; in this it is much like contemporary propositional calculi. We may In fact, consider alpha to contain, among its signs, "propositional variables" directly analogous to those of the ordinary PC; Peirce himself employs letters of the Roman alphabet in his alpha graphs much as we use propositional variables in the PC.
We remarked earlier that comparisons could be drawn between Peirce's division of the existential graphs and division of the algebra of logic. In such a comparison. the beta graphs would be juxtaposed to the "first-intentional logic of relatives" In the one case as in the other, we enter the field. of "analysed atomic sentences," sentences which contain a predicate and signs representing individuals for which the predicate holds iff the sentence is true. Peirce's favorite term for such a predicate is "rhema," or "rheme" (3.420 ff., 4.438 ff.). ' "unanalyzed expression" of a rheme in the systems of existential graphs -- specifically, in beta -- is called by Peirce a "spot" (4.403, 4.441). Some explication may be in order. A rheme is "a blank form of proposition produced by . . . erasures [the spaces left by which] can be filled, each with a proper name, to make a proposition again" (4.431). In other words, "_____ is good." and "_____ gives _____ to _____" are examples of rhemes, the first being monadic (or unary) and the other triadic (or ternary). we see from 4.438 that Peirce recognizes a 0-adic rheme, a rheme which, since it contains no blanks, is already a sentence; the unanalysed expression in in the system of graphs of such a rheme might be considered to be one of the "atomic graphs" of alpha.
The "spot," then, as the unanalysed expression of a rheme with one or more blanks, would be a kind of predicate symbol, analogous to symbols with that function in the predicate calculus of today.
Peirce specifies that "on the periphery of every spot, a certain place shall be appropriated to each blank of the rheme, and such a place shall be called a 'hook' of the spot" (4.403). He wished the graphs to be graphic; the hooks are to be conceived of as connecting the predicate in question to the signs representing the individuals of which it is true.
|
|
| Binary Spot with "Dots" Attached to its Hooks |
Strangely enough, however, we shall not in practice see these hooks; in any graph properly so called, all hooks are already filled, connected to the appropriate signs for individuals. A spot with empty hooks would not even be analogous to an open sentence in the predicate calculus; it would rather be like the non-well-formed-formula which an n-ary predicate followed by fewer than n individual variables would be.
When we come to the method of representation of individuals in beta, we come to a point of marked difference between the notation of beta and that of ordinary predicate calculi. In an ordinary predicate calculus, individuals are referred to by individual variables, which variables are capable of standing as arguments of predicates of the system. in beta, however,
A heavy dot attached at the hook of a spot shall be understood as filling the corresponding blank of the rheme of the spot with an indefinite sign of an individual, so that when there is a dot attached to every hook; the result shall be a proposition (4.404).
and further (we state paragraphs directly from CP):
4.405. A very heavily marked point whether isolated, the extremity of a heavy line or at the furcation of a heavy line, shall denote a single individual without itself indicating what individual it is.
4.406 A heavily marked line without any sort of interruption . . . shall, under the name of a line of identity, be a graph subject to all the conventions relating to graphs, and asserting precisely the identity of the individuals denoted by its extremities.
Instead of representing individuals by means of letters of the alphabet, beta uses "dots," and it asserts the identity of what is represented, by one dot and what is represented by another by the simple device of allowing each to stand as the terminal of a heavy line drawn on the SA.
|
|
| Unary Spots Connected by "Line of Identity" |
In practice we shall find that much of Peirce's complex terminology for these may be avoided; instead of speaking of "dots," "ligatures," and like terminological complexities which Peirce seemed to delight in using, we shall find that we can get by with the notion of line of identity alone -- for which see chapter II.
Peirce also provides a subsidiary means of representing individuals in beta. I say "subsidiary," because -- in 4.460, for example -- he advocates it as an alternate notation whose purpose is to avoid complex tangles of lines of identity, This notation is the "selective." A selective is a sign, normally a letter of the Roman alphabet, which actually resembles in appearance and behavior the (bound) individual variable of the ordinary predicate calculus. But Peirce felt that the use of the selective can be avoided (as indeed it can -- see 4.462), and should be avoided (4.473, 4.561n). As we shall see in the final section of this introduction, Peirce's preference for the line of identity to the exclusion of the selective and his reasons for this preference offer us important clues as to why he considered the existential graphs to be so important.
 |
 |
| A Graph with a Line of Identity | The Same Graph with the LI Replaced by Selectives |
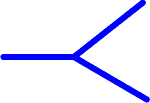
In 4.406 Peirce informs us that "a point upon which three lines of identity abut is a graph expressing the relation of teridentity." As Peirce indicates in 4.445, this sign -- the branching of a line of identity -- gives us the apparatus for identifying any number of points on the sheet.
 |
| A Branching |
One more bit of Peircean terminology may be mentioned at this point; a "network" of lines of identity, all of which are connected to each other and which may cross cuts and contain branchings is called by Peirce a "ligature" (4.407). The ligature, or network of lines of identity, ties together as representing the same individual all the points along its length, but it is not necessarily itself a graph. We might note here that Peirce was loath to say flatly that a line of identity is capable of crossing a cut (4.401, 4.406), and so had to develop elaborate conventions to account for what happens when a line of identity appears to cross a cut. We shall find in chapter II, however, that we may so set things up that we may think of lines of identity as crossing cuts and so avoid some of the terminology and conventions which Peirce feels it is necessary to use.
At this point we come to another distinctive feature of the beta graphs. Peirce formulated the system not only so that it contained signs for predicates and for individuals, but so that it would be able to quantify over the individuals represented as well. This is accomplished quite simply::
Any line of identity whose outermost part is evenly enclosed [that is, by an even number of or by no cuts] refers to something, and any one whose outermost part is oddly enclosed [that is, by an odd number of cuts] refers to anything there might be (4.458).
The type of quantification applying to a given line of identity, then, is determined by examining the line and noting how many cuts enclose the least-enclosed part of the line. The very interesting feature here is that no explicit sign for quantification -- that is, no quantifier -- is required to "get quantification" in beta.
Although this by no means has been an exhaustive catalogue of the signs of the existential graphs, it will suffice as an introduction to the notation. Mention will be made of other signs at appropriate points in the text.
Transformations in the Existential Graphs
We are now in possession of a considerable number of signs of the graphs. The next step is to see how these signs work. As we remarked earlier, the starting point in alpha for our purposes is simply a blank SA. Casting about for an interpretation of a blank SA, we might take it as an exemplification of "He who says nothing does not lie"; or, since a blank SA is to be considered a graph, and so is to be taken as asserting something, as being a proposition, we might interpret it as asserting -- in Fregean fashion -- "The True" (or perhaps we might prefer to say "denoting" here rather than "asserting" -- from this point of view, the blank SA would be a "pure denotation" of "The True," with no connotation at all).
For the purposes of beta, one additional starting point or "axiomatic graph" is to be considered. Peirce states that
since a Dot [the dot may here be considered a limiting case of the "freestanding" line of identity] merely asserts that some individual object exists . . . it may be inserted in any Area (4.567).
This amounts to an axiomatic assertion of the "dot" -- or of the simple line of identity with no branchings and no connections, situated entirely in one area. The "assertion of the dot" amounts to a declaration of the non-emptyness of the beta universe of discourse. We thus see that the "axioms" required for alpha and beta s we shall study them are of the very simplest and most elementary kind.
For gamma as its signs have been presented, Peirce offers no additional axiomatic graphs. We shall find in our detailed examination of parts of gamma in chapter III, however, that some interesting systems may be evolved in the notation of gamma through the use of certain such graphs.
We shall now list the "rules of transformation"(n1) for the graphs essentially as we shall employ them in this paper; if the systems of graphs are considered systems of logic, these rules of transformation are, in effect, the rules of inference of the logics involved. Those rules will enable us to produce "proofs" of "theorems" within these logics, taking the first step of any proof as the appropriate "axiomatic graph" mentioned above. The principal references in Peirce for these rules are 4.492, 4.505, and 4.516. Note that we shall employ a decimal system in numbering these rules, using 0 as the number to the left of the decimal point; the purpose of this is to make the numbering of these rules consistent with the numbering of the lemmas, metatheorems, and corollaries of the following chapters. Following are the rules for alpha:
| 0.01 | In any area of the sheet enclosed by an odd number of cuts any graph may be scribed (This is the rule of "Insertion in Odd"). |
| 0.02 | In any area of the sheet enclosed by an even number of, or by no cuts, any graph may be erased (rule of "Erasure in Even"). |
| 0.03 | If a graph X occurs in any area of the sheet, X may be iterated (that is, "written again") in that same area or in any area enclosed by at least all the cuts by which the original occurrence of X was enclosed (rule of "Iteration"). |
| 0.04 | This rule is the exact converse of 0.03 -- it is the rule of "Deiteration." |
| 0.05 | Any graph occurring in any area of the sheet may have scribed about it two cuts; there is to be no graph in the annular space between the cuts thus inserted (rule of "Biclosure"). |
| 0.06 | This rule is the exact converse of 0.05 -- this is the rule of "Negative Biclosure" Note that two cuts removed by this rule are to have nothing in the annular space between them. |
We shall now turn to the rules of transformation for the beta system. These are rules designed specifically to handle transformations involving lines of identity; it will be noted that they closely parallel the alpha rules given above, and might, in fact be considered clauses extending the alpha rules to deal with lines of identity. We will here remark, by the way, that following our statement of the rules for beta and for gamma, we shall present some illustrations of the applications of these rules. These, then, are the rules which in addition to 0.01-0.06 above are needed for the beta system:
| 0.07 | In any area enclosed by an odd number of cuts, two "loose ends" of lines of identity may be joined (rule of "joining in odd"). | ||||||||
| 0.08 | In any area enclosed by an even number of cuts, or by no cuts, any line of identity may be broken by erasing a portion of it (rule of "breaking in even"). | ||||||||
| 0.09 |
|
||||||||
| 0.10 | This rule is the exact converse of 0.09; it has three clauses corresponding to those of 0.09. and it may be called the rule of "beta deiteration." | ||||||||
| 0.11 | Any graph may be enclosed by two cuts as in 0.05, with the added provision that lines of identity may pass from entirely outside the outer to entirely inside the inner cut; all they are allowed is "free direct passage" through the annular space between the cuts. Aside from such lines of identity -- which may not even branch within the annular space -- no sign of any kind is permitted between the two cuts [when they are scribed]. This rule may be called "beta biclosure." | ||||||||
| 0.12 | This rule is the exact converse of 0.11; it may be called "negative beta biclosure." It permits the removal of two cuts which might have been inserted by 0.11. | ||||||||
We shall state now the rules which Peirce offers for transformations involving the "broken cut" of gamma. We shall comment at length on these rules in chapter III of this paper. These rules are drawn from 4.516:
| 0.13 | In a broken cut already on SA any graph may be inserted. |
| 0.14 | A broken cut in an area enclosed by an odd number of cuts (which may be either alpha or broken cuts) may be transformed to an alpha cut (by "filling in" the breaks in it). |
| 0.15 | An alpha cut in an area enclosed by an even number of or by no cuts may be transformed to a broken cut (by erasing parts of it). |
We shall now present some simple examples of transformations permitted by the above rules. Note that the "right arrow" -- ® -- indicates permission to transform "in one direction only." The "double arrow" -- « -- indicates "intertransformability." The examples then are:
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
I have considered it unnecessary to offer an example of 0.13. It should be clear by now that the alpha cut is very close in it function to the negation sign of the Classical Propositional Calculus -- the rules of biclosure are the most obvious indication of this. Again, the simultaneous occurrence of a number of graphs may be interpreted as the conjunction of the sentences represented by those graphs. The spots of the beta system behave much like the predicates of the ordinary first-order calculus; the line of identity, however, is a sign with a very complex usage in beta, as should now be evident. It behaves sometimes like a variable, sometimes like a sentence, and sometimes like a quantifier. We shall investigate, in detail and formally, the alpha and beta systems in chapters I and II respectively. In chapter III we shall enter into a study of certain systems which may be classified as gamma systems. But before we do this, before we begin to make use of the "raw material" we have presented up to this point, we shall take a quick look at the existential graphs as they stand in the philosophy of Peirce.
The Continuity Interpretation
The systems of existential graphs are, as we shall see, systems of logic, and systems of logic in a very well-defined sense. Peirce had developed logics along more ordinary lines before he began his work on the graphs; nevertheless, he clearly preferred the graphs to his algebras of logic. As we quoted Peirce a bit earlier:
[The development of a thorough understanding of mathematical reasoning] is the purpose for which my logical algebras were designed, but which, in my opinion, they do not sufficiently fulfill. The present system of existential graphs is far more perfect in that respect (4.429).
But why on earth did he believe that? What is there in the notation of the graphs that, for Peirce, makes them superior to the ordinary logical algebras? It should be understood, first of all, that "mathematical reasoning" covers considerable ground for Peirce. His definition of mathematics was "the science which draws necessary conclusions" (4.229). "Mathematical reasoning," then, in the broadest sense, is deductive reasoning, and Peirce's comments in 4.228 indicate to us that he did not wish to restrict it to a narrower notion in this case. And we find Peirce stating that "mathematics meddles with every other sciences without exception. There is no science whatever to which is not attached an application of mathematics" (1.245). For Peirce, this is virtually equivalent to saying that mathematical or deductive reasoning is an integral part of reality itself. The development of a thorough understanding of mathematical reasoning is a first and absolutely essential step towards the development of a thorough understanding of reality. The algebras of logic and the graphs were to foster such an understanding by presenting an analysis of the deductive process, by "breaking up inferences into the greatest possible number of steps, and exhibiting them under the most general categories possible" (4.373).
And for the analysis of the deductive process, Peirce preferred the systems of existential graphs to the algebras of logic. We can get a clue to the reasons for this preference by investigating a passage in which he discusses certain of the signs of the graphs. We will recall that we earlier mentioned a sign of the beta system called the "selective." the selective, as we noted, is used in many places where a line of identity might be used; it is, however, much like the ordinary bound variable of the algebras of logic -- rather than being a line, it is simply a letter of the alphabet. Peirce criticises the selective as a sign of the graphical systems; this criticism of the selective may be applied directly to the variables of the algebras of logic to give a strong indication of why he preferred the graphs to those algebras. "The first respect," he states," in which Selectives are not as analytical as they might be, and therefore ought to be, is in representing identity" (4.561n). Peirce remarks here that the way that two occurrences of a given selective (and the same would be true for two occurrences of a variable in an algebra) represent the same object is by "a special convention of interpretation." Peirce feels that given two occurrences of such a selective -- or variable -- although we know by convention that they are to be considered to represent the same object, "There is here no analysis of identity" (4.561n). Peirce wants a sign which will not merely be conventionally understood as signifying identity, but which will "wear its meaning on its sleeve," so to speak; which will offer in its very representation of identity an analysis of identity. And "the line of identity which may be substituted for the selectives very explicitly represents identity to belong to the genus Continuity and to the species Linear Continuity" (4.561n). Identity is a continuity, and so too is an unbroken line. The self-identical individual is far better represented, Peirce felt, by a continuous line than by a batch of discrete occurrences of an individual variable, provided only a formalism can be found which gives the line the powers that the representative of an individual should have. In Peirce's opinion the beta formalism does the trick, and so the beta line of identity is far superior to the selective or the ordinary variable to represent the self-identical individual. And Peirce goes even further in telling us about this representing function of the graphs: "The continuity of [the sheet of assertion] being two dimensional . . . should represent an external continuity, and especially an continuity of experiential appearance" (4.561n). And the sheet of assertion,
in representing the field of attention, represents the general object of tat attention, the Universe of Discourse. This being the case, the continuity of the [sheet of assertion] in those places where, nothing being scribed, no particular attention is paid, is the most appropriate icon possible of the continuity of the Universe of Discourse where it only receives general attention as that Universe (4.561n).
We see from these remarks that Peirce felt that the graphs had a certain natural appropriateness about them for the task which he set them to do, and we see further that he felt that the continuity present in certain basic symbols of the graphs was the factor that made the graphs superior to the logical algebras for that task of representation and analysis.
Now the alpha and beta sheets of assertion represent simply a universe of existent individuals, and the different parts of the sheet represent facts or true assertions made concerning that universe. At the cuts we pass into other areas, areas of conceived propositions which are not realized (4.512).
The cuts are discontinuities on the sheet of assertion, and they are meant by Peirce to correspond to "discontinuities of the universe of discourse." The non-existent, the unrealized, is in a definite sense discontinuous with the existent and realized insofar as it is not part of the universe of existent individuals. In general, a cut is a break in the continuity of any area indicates a certain break in continuity between what is inside and what is outside of it. The contents of a cut on the alpha or beta sheet of assertion represents that which is not part of the "continuity of experiential appearance."
In attempting to get across the idea of how the graphs represent, Peirce states:
You may regard the ordinary blank sheet of assertion as a film upon which there is, as it were, an undeveloped photograph of the facts in the universe. I do not mean a literal picture, because its elements as propositions and the meaning of a proposition is abstract and altogether of a different nature from a picture. But I ask you to imagine all the true propositions to have been formulated; an since facts blend into one another, it can only be in a continuum that we can conceive this to be done. . . . Of this continuum the blank sheet of assertion may be imagined to be a photograph (4.512).
Peirce then states, "So far I have called the sheet a photograph, so as not to overwhelm you with all the difficulties of the conception at once. But let us rather call it a map" (4.513) And just what is a map? Well, "a map of the simplest kind represents all the points of one surface by corresponding points of another surface in such a manner as to preserve the continuity unbroken, however great may be the distortion" (4.513). It is hardly necessary to add that if an existential graph is a map, it is not the "simplest kind" of map. Point in a given graph are intended to be correlated with what may loosely be called "features of the universe of discourse represented by the sheet of assertion upon which that graph is scribed," rather than with "points of another surface." If "_____ is red" and "_____ is round" are beta spots, they are to be correlated with the properties of being red and being round; it is quite clear that in the actual existing universe we do not have "redness" and "roundness" floating about as "things in themselves," without individuals that are red or round. This jibes with Peirce's refusal to call a spot whose hooks are empty a graph (4.439). But let the two spots mentioned be connected by a line of identity and we do have a graph, the graphs which states, "There is something both red and round." The continuity of the line of identity between spots expresses, for Peirce, the continuity which is the self-identity of the thing which is both red and round. It is thus that the graphs are to be considered "maps"; they are not pictures of facts -- for who ever saw a fact that looked like an existential graph -- but they are supposed to indicate continuity where there is continuity, and to represent discontinuity where there is discontinuity. A break in a line of identity is one such representation of discontinuity; the cut, as we have remarked, is another, of another kind.
All this emphasis on continuity is by no means accidental. The Peirce of the existential graphs, especially of the passages from which we have been quoting, is as well the Peirce of synechism.(n1) It is unquestionable that "continuity" is the key word of Peirce's synechism -- all that is real is, insofar as it is real, continuous in some way or another. One passage, perhaps, will emphasize Peirce's rather firm commitment to the notion of continuity as a heuristic tool:
Upon the assault of the enemy, when pressed for the explanation of any fact, I lock myself up in my castle of impregnable logic and squirt out melted continuity upon the heads of my besiegers below.(n1)
And closely connected to synechism is what Peirce sometimes called "synectics," but which is better known by the name of "topology." Murphey states, in fact, that
the model upon which Peirce based his metaphysics quite obviously is the topology of Listing. And this is in fact what one would expect, for his work in mathematics had led him to the conclusion that topology is the mathematics of pure continua. If there is any formal system which ought to provide the key to the synechistic world, it is synectics or topology.(n2)
There is no doubt whatever that Peirce in his later years was fascinated by topology, even though the only topology he knew was that of Listing, which was a rather low octane brand. It is also clear that he thought topology to be the mathematics of pure continua, and that continuity has a key place in his philosophy. The only point in doubt is just how Peirce planned to correlate the "synechistic world" with Listing's topology. For it is far from evident how we get from "continuity is the master key, and topology is the mathematics of pure continua" to "topology is the master key." Murphey does not feel that Peirce was able to make this particular jump successfully, and I would tend to agree with Murphey. But the interesting thing from our point of view is how Peirce attempted that jump. I submit that Peirce tried it in a manner which, apparently, did not strike Murphey. It was through the existential graphs, I suggest, that Peirce tried to see the was from "the mathematics of pure continua" to "the synechistic world" -- those same existential graphs that Murphey dismisses as merely one of the factors in Peirce's "lack of philosophical productivity" at the close of the nineteenth century.(n1)
Peirce's "Algebra of Logic" owes its name and a large part of its form to what, in the later nineteenth century, became the algebra of real numbers. Although there are similarities between the algebra of logic and the algebra of real numbers, there is no doubt that they are different branches of mathematics. It seems to me that the relation between the existential graphs and Listing's topology is a very similar kind of thing. Peirce never indicates that the graphs are topology, even though it is very difficult to look at his presentations of them without thinking of topology. The graphs, in fact, rather than being a topological system, were to help us reason about topology and solve its problems, much as they were to help us solve the problems of mathematical reasoning in general (4.428). But much as the algebra of logic was fashioned after the image of the algebra of real numbers, I believe that the existential graphs were fashioned after the image of Listing's topology. As what became the algebra of real numbers offered the algebra of logic a "pattern" into which its signs should fall and an indication of how its signs should behave, Listing's topology offered the existential graphs a pattern into which their signs should fall and an indication of the way their signs should behave. Where the systems of 3.359 ff., for example, constitute an "algebra of logic," the existential graphs constitute a "topology of logic." And it is the features that they share with topology that render the graphs superior as a logical system, in the Peircean sense, to the algebra of logic.
Thus, while topology was, for Peirce, the mathematics of pure continua, the existential graphs were the apparatus for representing symbolically the world of continua, the world of reality. Listing's topology of itself offered little more help to Peirce's project of synechism than did real number algebra, of itself. It was necessary for Peirce to develop a logic of continua, a system which would permit a mapping of the continua of reality into itself. This, I feel, is the reason why Peirce in his later years put so much work into the graphs. And this too, I am sure, is the explanation for that puzzling "subtitle" which Peirce attached to the systems of graphs -- "My chef d'oeuvre." The study of logical systems for their own sake as formal, mathematical systems was far from the chief interest of C. S. Peirce; hence it is unlikely that he would consider the graphs his major work because they are interesting formal systems. His fascination with and regard for the graphs goes beyond that; he saw for them, I am sure, a key place in his synechism. More than just a hint of this is given in a passage with which Peirce concludes a discussion of "An Improvement on the Gamma Graphs" (4.573 ff.):
We here reach a point at which novel considerations about the constitution of knowledge and therefore of the constitution of nature burst in upon the mind with cataclysmical multitude and resistlessness. It is that synthesis of tychism and pragmatism for which I long ago proposed the name, Synechism, to which one thus returns; but this time with stronger reasons than ever before (4.584).
But so far we have explicitly mentioned only the alpha and beta graphs in their "continuity interpretation." The alpha-beta sheet of assertion was to be considered as representing a very specific universe of discourse, the "universe of actual existent fact" (4.514). Synechism, however, was concerned with far more than this. Any "account of reality," in fact, which stopped with the actually existing universe and said nothing of the realm of possibility must, from the synechistic point of view, be radically incomplete. If we are correct about the place of the graphs in the thought of Peirce, then, we would expect him to have make provision for "the worlds of the possible" in his presentation of the graphs. He dud just his; gamma was to be the system which did for reality as a whole what he felt that alpha and beta did for the "universe of actual existent fact." We have seen that the alpha and beta sheet of assertion, a two-dimensional "space," a surface, was to represent this "universe of actual existent fact" although strictly speaking, at least three dimensions are required for a complete representation of beta, since there are instances when lines of identity are to be considered as crossing each other without joining; this offers no difficulties for what follows, for we can replace "surface" with "three-dimensional space," and "three-dimensional space" with "four-dimensional space" with no difficulty at all. Peirce, taking the alpha or beta SA as a surface, remarks:
. . . in order to represent to our minds the relation between the universe of possibilities and the universe of actual existent facts, if we are going to think of the latter as a surface, we must think of the former as a three-dimensional space in which any surface would represent all the facts that might exist in one existential universe (4.514).
Gamma, then, is -- quite literally -- to add another dimension to the existential graphs. For gamma was to be the system which supplied the formalism necessary for the symbolic expression of the relationships between different universes of discourse. Alpha and beta are to offer an analysis of the "deductive [mathematical] reasoning" of the continua of the actually existing universe, but gamma was supposed to present an analysis of the deductive process existing between and relating the possible universes of discourse, including the actual existing universe of the alpha-beta sheet. The importance for Peirce of gamma must not be understated. The universe of "actual existent fact" does not exist in a vacuum, nor did it spring full-panoplied from the head of Zeus. What is today an "existent fact" may yesterday have been a "not-yet-realized fact," a possibility; today it is in the realm of alpha and beta, while yesterday it was not -- what is the connection between that fact as of yesterday it was not -- what is the connection between that fact as of yesterday and as of today? The synechistic explanation must be that at both instances that fact must be part of a continuum which -- unlike the continua represented an alpha and beta -- transcends universes of discourse. But what is that continuum, and how are we to represent continua of that sort? This is the problem which gamma was to solve when it had been "brought to perfection." But how are we to go about the representations required of gamma? Peirce suggests that in order to handle the extra dimension required of gamma, we take as our gamma "sheet of assertion" not a single sheet, but "a book of separate sheets, tacked together at points, if not otherwise connected" (4.512) We are asked to think of the cut as being literally a cutting of the paper, which extends "down to one or another depth into the paper, so that the overturning of the piece cut out may expose one stratum or another, those being distinguished by their tints; the different tints representing different kinds of possibility" (4.578). The operation of "scribing" a cut now consists of two steps, cutting through the paper and turning over the portion we have cut out. That which is written on the reverse side of any of the sheets is to be considered denied in the universe of discourse which that sheet represents (4.574). When the area on the reverse of one of the sheets is "turned up" by the scribing of a cut, the denial of any graphs scribed on that area is asserted for the universe of discourse connected with the sheet to which the area belongs. We can picture, in this system, a nest of cuts with different cuts belonging to it penetrating to different strata of the book of sheets and expressing an extremely complex modal graph. All kinds of possible denial and possible assertion would be involved, and the situation could be extremely confusing.
It could be extremely confusing, that is, unless Peirce is at least able to provide us with a comprehensive set of rules of transformation for gamma which will enable us to know exactly which cuts we are allowed to make and what we may write in which area. Well, Peirce tells us quite frankly that so far a gamma goes, he was "able to gain mere glimpses, sufficient only to show me its reality, and to rouse my intense curiosity, without giving me any real insight into it" (4.576). The truth is that he was not able to discover such a comprehensive set of rules. We can see just about where he intended to fit it into his synechism. We can see what he hoped to do with it, but we can see as well as he could that he was not able to realize those hopes. The final formulation of gamma was for Peirce an El Dorado, a golden city glistening just beneath the horizon.
Peirce set down a large number of signs which he considered within the scope of gamma. With most of these signs he did little more than to set them down. Since gamma was to be a logic of "second intentions," it is not strange at all that he set down signs of gamma which were to be a sort of metalanguage for the graphs. For gamma was to be able to reason about ideas, and if this was the case, some provision should be made in it for such signs. 4.524-529 offer examples of such symbols. An examination of these signs leads us to the conclusion that this project was presented by Peirce as one of the threads that his successors were going to have to weave into the warp of the completed gamma fabric. He gives us no specific rules for working with those signs, and tells us very little about how they are to be used.
There is also another suggestion, in 4.470, which is interesting but to which Peirce devotes very little time. Here he shows us a different kind of line of identity, one which expresses the identity of spots rather than of individuals. This is an intriguing move, since it strongly suggests at least the second order predicate calculus, with spots now acquiring quantifications. Peirce did very little with this idea, so far as I am able to determine, but it seems to me that there would not be too much of a problem in working it into a graphical system which would stand to the higher order calculi as beta stands to the first-order calculus. The continuity interpretation of the "spot line of identity" is fairly clear; it maps the continuity of a property or a relation. The redness of an apple is the same, in a sense, as the redness of my face if I am wrong; the continuity of the special line of identity introduced in 4.470 represents graphically this sameness. This sameness or continuity is not the same as the identity of individuals; although its representation is scribed upon the beta sheet of assertion, its "second intentional" nature seems to cause Peirce to classify it with the gamma signs. The same may be said of the "metalinguistic signs" mentioned above.
The metalinguistic and "higher-order" signs are, however, peripheral to the main thrust of gamma as envisioned by Peirce. As we noted, and as an examination of 4.510 ff. and 4.573 ff. will verify, gamma was for him, above all, the "three-dimensional," the multi-sheet system. As we also noted, he was unable to come even close to a complete formulation of rules for that system (the multi-sheet formulation is, I believe, doomed from the start by its very complexity if for no other reason). But he did try to make a start:
In endeavoring to begin the construction of the gamma part of the system of existential graphs, what I had to do was to select, from the enormous mass of ideas thus suggested, a small number convenient to work with. It did not seem to be convenient to use more than one actual sheet at one time; but it seemed that various different kinds of cuts would be wanted (4.514).
He then begins telling us about one of these cuts, the "broken cut," which we mentioned earlier in this introduction. In chapter III we shall study several interesting systems constructible with the use of the broken cut.
Before we get to chapter II, however, we will have to move through chapters I and II, in which we will view in detail the alpha and the beta systems respectively.