|
Existential
Graphs - 4.418-529 |
| |
| |
Chapter 4: On Existential
Graphs, Euler's Diagrams, and Logical Algebra |
| |
CHAPTER 4 |
| |
ON EXISTENTIAL GRAPHS,
EULER'S DIAGRAMS,
AND LOGICAL ALGEBRAP(*1) |
| |
§INTRODUCTION |
| 418. |
A diagram is a representamen
(*2)
which is predominantly an icon of
relations and is aided to be so by conventions.
Indices are also more or less
used. It should be carried out upon a perfectly
consistent system of
representation, founded upon a simple and easily
intelligible basic idea. |
| |
|
|
| 419. |
A graph is a superficial diagram composed of the sheet upon which
it is written or drawn, of spots or their equivalents, of lines of connection,
and (if need be) of enclosures. The type, which it is supposed more or less to
resemble, is the structural formula of the chemist. |
| |
|
|
| 420. |
A logical graph is a graph representing logical relations iconically, so as to be an aid to logical analysis. |
| |
|
|
| 421. |
An existential graph is a logical graph governed by a. system of
representation founded upon the idea that the sheet upon which it is written,
as well as every portion of that sheet, represents one recognized universe,
real or fictive, and that every graph drawn on that sheet, and not cut off from
the main body of it by an enclosure, represents some fact existing in that
universe, and represents it independently of the representation of another such
fact by any other graph written upon another part of the sheet, these graphs,
however, forming one composite graph. |
| |
|
|
| 422. |
No other system of existential graphs than that herein set forth
having hitherto been proposed, this one will need, for the present, no more
distinctive designation. Should such designation hereafter become desirable, I
desire that this system should be called the Existential System of 1897, in
which year I wrote an account of it and offered it for publication to the
Editor of The Monist, who declined it on the ground that it might later be
improved upon. No changes have been found desirable since that date, although
it has been under continual examination; but the exposition has been rendered
more formal. |
| |
|
|
| 423. |
The following exposition of this system will be arranged as
follows: Part I will explain the expression of ordinary forms of language in
graphs and the interpretation of the latter into the former in three sections,
as follows:
A will state all the fundamental conventions of the system, separating those which are essentially different, showing the need which each is designed to meet together with the reasons for meeting it by the particular convention chosen, so far as these can be given at this stage of the development. A complete discussion will be given in an Appendix
(*1) to this part. To aid the
understanding of all this, various logical analyses will be interspersed where they become pertinent.
B will enunciate other rules of interpretation whose validity will be demonstrated from the fundamental conventions as premisses. This section will also introduce certain modifications of some of the signs established in A, the modified signs being convenient, although good reasons forbid their being considered fundamental.
C will redescribe the system in a compact form, which, on account of its uniting into one many rules that had, in the first instance; to be considered separately, is more easily grasped and retained in the mind.
Part II will develop formal "rules," or permissions, by which one graph
may be transformed into another without danger of passing from truth to falsity
and without recurring to any interpretation of the graphs; such transformations
being of the nature of immediate inferences. The part will be divided into
sections corresponding to those of Part I.
A will prove the basic rules of transformation directly from the fundamental conventions of A of Part I.
B will deduce further rules of transformation from those of A, without further recourse to the principles of transformation.
C will restate the rules in more compact form.
Part III will show how the system may be made useful.(*1) |
| |
|
|
| |
Part I. PRINCIPLES OF INTERPRETATION
P |
| |
A. Fundamental Conventions
P |
| |
§1. OF CONVENTIONS NOS. 1 AND 2(*1)
P |
| 424. |
In order to understand why this system of expression has the
construction it has, it is indispensable to grasp the precise purpose of it,
and not to confuse this with four other purposes, to wit:
- First, although the study of it and practice with it will be highly
useful in helping to train the mind to accurate thinking, still that
consideration has not had any influence in determining the characters of the
signs employed; and an exposition of it, which should have that aim, ought to
be based upon psychological researches of which it is impossible here to take
account.
- Second, this system is not intended to serve as a universal language
for mathematicians or other reasoners, like that of Peano.
- Third, this system is not intended as a calculus, or apparatus by which
conclusions can be reached and problems solved with greater facility than by
more familiar systems of expression. Although some writers
(*2) have studied the
logical algebras invented by me with that end apparently in view, in my own
opinion their structure, as well as that of the present system, is quite
antagonistic to much utility of that sort. The principal desideratum in a
calculus is that it should be able to pass with security at one bound over a
series of difficult inferential steps. What these abbreviated inferences may
best be, will depend upon the special nature of the subject under discussion.
But in my algebras and graphs, far from anything of that sort being attempted,
the whole effort has been to dissect the operations of inference into as many
distinct steps as possible.
- Fourth, although there is a certain fascination about these graphs, and
the way they work is pretty enough, yet the system is not intended for a
plaything, as logical algebra has sometimes been made, but has a very serious
purpose which I proceed to explain.
|
| |
|
|
| 425. |
Admirable as the work of research of the special sciences --
physical and psychical -- is, as a whole, the reasoning [employed in them] is
of an elementary kind except when it is mathematical, and it is not
infrequently loose. The philosophical sciences are greatly inferior to the
special sciences in their reasoning. Mathematicians alone reason with great
subtlety and great precision. But hitherto nobody has succeeded in giving a
thoroughly satisfactory logical analysis of the reasoning of mathematics. That
is to say, although every step of the reasoning is evidently such that the
collective premisses cannot be true and yet the conclusion false, and although
for each such step, A, we are able to draw up a self-evident general rule that
from a premiss of such and such a form such and such a form of conclusion will
necessarily follow, this rule covering the particular inferential step, A, yet
nobody has drawn up a complete list of such rules covering all mathematical
inferences. It is true that mathematics has its calculus which solves problems
by rules which are fully proved; but, in the first place, for some branches of
the calculus those proofs have not been reduced to self-evident rules, and in
the second place, it is only routine work which can be done by simply following
the rules of the calculus, and every considerable step in mathematics is
performed in other ways. |
| |
|
|
| 426. |
If we consult the ordinary treatises on logic for an account of
necessary reasoning, all the help that they afford is the rules of syllogism.
They pretend that ordinary syllogism explains the reasoning of mathematics; and
books have professed to exhibit considerable parts of the reasoning of the
first book of Euclid's Elements stated in the form of syllogisms. But if this
statement is examined, it will be found that it represents transformations of
statements to be made that are not reduced to strict syllogistic form; and on
examination it will be found that it is precisely in these transformations that
the whole gist of the reasoning lies. The nearest approach to a logical
analysis of mathematical reasoning that has ever been made was Schröder's
statement, with improvements, in a logical algebra of my invention, of
Dedekind's reasoning (itself in a sort of logical form) concerning the
foundations of arithmetic.(*1) But though this relates only to an exceptionally
simple kind of mathematics, my opinion -- quite against my natural leanings
toward my own creation -- is that the soul of the reasoning has even here not
been caught in the logical net. |
| |
|
|
| 427. |
No other book has, during the nineteenth century, been deeply
studied by so large a proportion of the strong intellects of the civilized
world as Kant's Critic of the Pure Reason; and the reason has undoubtedly been
that they have all been greatly struck by Kant's logical power. Yet Kant, for
all this unquestionable power, had paid so little attention to logic that he
makes it manifest that he supposed that ordinary syllogism explains
mathematical reasoning, and indeed [in] the simplest mood of syllogism,
Barbara. Now, at the very utmost, from n propositions only 1/4n2 conclusions
can be drawn by Barbara. In the thirteen books of Euclid's Elements there [are]
14 premisses (5 postulates and 9 axioms) excluding the definitions, which are
merely verbal. Therefore, even if these premisses were related to one another
in the most favorable way, which is far from being the case, there could only
be 49 conclusions from them. But Euclid draws over ten times that number (465
propositions, 27 corollaries, and 17 lemmas) besides which his editors have
inserted hundreds of corollaries. There are 48 propositions in the first book.
Moreover, in Barbara or any sorites, or complexus of such syllogisms, to
introduce the same premiss twice is idle. But throughout mathematics the same
premisses are used over and over again. Moreover a person of fairly good mind
and some logical training will instantly see the syllogistic conclusions from
any number of premisses. But this is far from being true of mathematical
inferences. |
| |
|
|
| 428. |
There is reason to believe that a thorough understanding of the
nature of mathematical reasoning would lead to great improvements in
mathematics. For when a new discovery is made in mathematics, the demonstration
first found is almost always replaced later by another much simpler. Now it may
be expected that, if the reasoning were thoroughly understood, the unnecessary
complications of the first proof would be eliminable at once. Indeed, one might
expect that the shortest route would be taken at the outset. Then again,
consider the state of topical geometry, or geometrical topics, otherwise called
topology. Here is a branch of geometry which not only leaves out of
consideration the proportions of the different dimensions of figures and the
magnitudes of angles (as does also graphics, or projective geometry --
perspective, etc.) but also leaves out of account the straightness or mode of
curvature of lines and the flatness or mode of bending of surfaces, and
confines itself entirely to the connexions of the parts of figures
(distinguishing, for example, a ring from a ball). Ordinary metric geometry
equally depends on the connections of parts; but it depends on much besides.
It, therefore, is a far more complicated subject, and can hardly fail to be of
its own nature much the more difficult. And yet geometrical topics stands idle
with problems to all appearance very simple staring it unsolved in the face,
merely because mathematicians have not found out how to reason about it. Now a
thorough understanding of mathematical reasoning must be a long stride toward
enabling us to find a method of reasoning about this subject as well, very
likely, as about other subjects that are not even recognized to be
mathematical. |
| |
|
|
| 429. |
This, then, is the purpose for which my logical algebras were
designed but which, in my opinion, they do not sufficiently fulfill. The
present system of existential graphs is far more perfect in that respect, and
has already taught me much about mathematical reasoning. Whether or not it will
explain all mathematical inferences is not yet known.
Our purpose, then, is to study the workings of necessary inference.
What we want, in order to do this, is a method of representing diagrammatically
any possible set of premisses, this diagram to be such that we can observe the
transformation of these premisses into the conclusion by a series of steps each
of the utmost possible simplicity. |
| |
|
|
| 430. |
What we have to do, therefore, is to form a perfectly consistent
method of expressing any assertion diagrammatically. The diagram must then
evidently be something that we can see and contemplate. Now what we see appears
spread out as upon a sheet. Consequently our diagram must be drawn upon a
sheet. We must appropriate a sheet to the purpose, and the diagram drawn or
written on the sheet is to express an assertion. We can, then, approximately
call this sheet our sheet of assertion. The entire graph, or all that is drawn
on the sheet, is to express a proposition, which the act of writing is to
assert. |
| |
|
|
| 431. |
But what are
our assertions to be about? The answer must be that they
are to be about an arbitrarily hypothetical universe, a
creation of a mind. For it is necessary
reasoning alone that we intend to study; and the
necessity of such reasoning consists in this, that not
only does the conclusion happen to be true of a
pre-determinate universe, but will be true, so
long as the premisses are true, howsoever the universe may subsequently turn out to be
determined. Thus, conformity to an existing, that is, entirely determinate,
universe does not make necessity, which consists in what always will be, that
is, what is determinately true of a universe not yet entirely determinate.
Physical necessity consists in the fact that whatever may happen will conform
to a law of nature; and logical necessity, which is what we have here to deal
with, consists of something being determinately true of a universe not entirely
determinate as to what is true, and thus not existent. In order to fix our
ideas, we may imagine that there are two persons, one of whom, called the grapheus, creates the universe by the continuous development of his idea of it,
every interval of time during the process adding some fact to the universe,
that is, affording justification for some assertion, although, the process
being continuous, these facts are not distinct from one another in their mode
of being, as the propositions, which state some of them, are. As fast as this
process in the mind of the grapheus takes place, that which is thought acquires
being, that is, perfect definiteness, in the sense that the effect of what, is
thought in any lapse of time, however short, is definitive and irrevocable; but
it is not until the whole operation of creation is complete that the universe
acquires existence, that is, entire determinateness, in the sense that nothing
remains undecided. The other of the two persons concerned, called the graphist,
is occupied during the process of creation in making successive modifications
(i.e., not by a continuous process, since each modification, unless it be
final, has another that follows next after it), of the entire graph.
Remembering that the entire graph is whatever is, at any time, expressed in
this system on the sheet of assertion, we may note that before anything has
been drawn on the sheet, the blank is, by that definition, a graph. It may be
considered as the expression of whatever must be well-understood between the graphist and the interpreter of the graph before the latter can understand what
to expect of the graph. There must be an interpreter, since the graph, like
every sign founded on convention, only has the sort of being that it has if it
is interpreted; for a conventional sign is neither a mass of ink on a piece of
paper or any other individual existence, nor is it an image present to
consciousness, but is a special habit or rule of interpretation and consists
precisely in the fact that certain sorts of ink spots -- which I call its
replicas -- will have certain effects on the conduct, mental and bodily, of the
interpreter. So, then, the blank of the blank sheet may be considered as
expressing that the universe, in process of creation by the grapheus, is
perfectly definite and entirely determinate, etc. Hence, even the first writing
of a graph on the sheet is a modification of the graph already written. The
business of the graphist is supposed to come to an end before the work of
creation is accomplished. He is supposed to be a mind-reader to such an extent
that he knows some (perhaps all) the creative work of the grapheus so far as it
has gone, but not what is to come. What he intends the graph to express
concerns the universe as it will be when it comes to exist. If he risks an
assertion for which he has no warrant in what the grapheus has yet thought, it
may or may not prove true. |
| |
|
|
| 432. |
The above
considerations constitute a sufficient reason for
adopting the following convention, which is hereby
adopted:
Convention No. 1. A certain sheet, called the sheet of assertion, is
appropriated to the drawing upon it of such graphs that whatever may be at any
time drawn upon it, called the entire graph, shall be regarded as expressing an
assertion by an imaginary person, called the graphist, concerning a universe,
perfectly definite and entirely determinate, but the arbitrary creation of an
imaginary mind, called the grapheus. |
| |
|
|
| 433. |
The convention which has next to be considered is the most
arbitrary of all. It is, nevertheless, founded on two good reasons. A diagram
ought to be as iconic as possible; that is, it should represent relations by
visible relations analogous to them. Now suppose the graphist finds himself
authorized to write each of two entire graphs. Say, for example, that he can
draw:
The pulp of some oranges is red;
and that he is equally authorized to draw:
To express oneself naturally is the last perfection
of a writer's art.
Each proposition is true independently of the other, and either may therefore
be expressed on the sheet of assertion. If both are written on different parts
of the sheet of assertion, the independent presence on the sheet of the two
expressions is analogous to the independent truth of the two propositions that
they would, when written separately, assert. It would, therefore, be a highly
iconic mode of representation to understand,
The pulp of some oranges is red.
To express oneself naturally is the last perfection of a writer's art.
where both are written on different parts of the sheet, as the assertion of
both propositions. |
| |
|
|
| 434. |
It is a subsidiary recommendation of a mode of diagrammatization,
but one which ought to be accorded some weight, that it is one that the nature
and habits of our minds will cause us at once to understand, without our being
put to the trouble of remembering a rule that has no relation to our natural
and habitual ways of expression. Certainly, no convention of representation
could possess this merit in a higher degree than the plan of writing both of
two assertions in order to express the truth of both. It is so very natural,
that all who have ever used letters or almost any method of graphic
communication have resorted to it. It seems almost unavoidable, although in my
first invented system of graphs, which I call entitative graphs,(*1)
propositions
written on the sheet together were not understood to be independently asserted
but to be alternatively asserted. The consequence was that a blank sheet
instead of expressing only what was taken for granted had to be interpreted as
an absurdity. One system seems to be about as good as the other, except that
unnaturalness and aniconicity haunt every part of the system of entitative
graphs, which is a curious example of how late a development simplicity is.
These two reasons will suffice to make every reader very willing to accede to
the following convention, which is hereby adopted. Convention No. 2. Graphs on different parts of the sheet, called
partial graphs, shall independently assert what they would severally assert,
were each the entire graph. |
| |
|
|
| |
§2. OF CONVENTION NO. 3
P |
| 435. |
If a system of expression is to be adequate to the analysis of all
necessary consequences,(*P1) it is requisite that it should be able to express
that an expressed consequent, C, follows necessarily from an expressed
antecedent, A. The conventions hitherto adopted do not enable us to express
this. In order to form a new and reasonable convention for this purpose we must
get a perfectly distinct idea of what it means to say that a consequent follows
from an antecedent. It means that in adding to an assertion of the antecedent
an assertion of the consequent we shall be proceeding upon a general principle
whose application will never convert a true assertion into a false one. This,
of course, means that so it will be in the universe of which alone we are
speaking. But when we talk logic -- and people occasionally insert logical
remarks into ordinary discourse -- our universe is that universe which embraces
all others, namely The Truth, so that, in such a case, we mean that in no
universe whatever will the addition of the assertion of the consequent to the
assertion of the antecedent be a conversion of a true proposition into a false
one. But before we can express any proposition referring to a general
principle, or, as we say, to a "range of possibility," we must first find means
to express the simplest kind of conditional proposition, the conditional de inesse, in which "If A is true, C is true" means only that, principle or no
principle, the addition to an assertion of A of an assertion of C will not be a
conversion of a true assertion into a false one. That is, it asserts that the
graph of Fig. 69, anywhere on the sheet of assertion, might be transformed into
the graph of Fig. 70 without passing from truth to falsity. |
| |
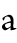 |
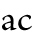 |
|
Figure 69 |
Figure 70 |
|
| |
This conditional
de inesse has to be expressed as a graph in such a way as
distinctly to express in our system both a and c, and to exhibit their relation
to one another. To assert the graph thus expressing the conditional de inesse,
it must be drawn upon the sheet of assertion, and in this graph the expressions
of a and of c must appear; and yet neither a nor c must be drawn upon the sheet
of assertion. How is this to be managed? Let us draw a closed line which we may
call a sep (sæpes, a fence), which shall cut off its contents from the sheet of
assertion. Let this sep together with all that is within it, considered as a
whole, be called an enclosure, this close, being written on the sheet of
assertion, shall assert the conditional de inesse; but that which it encloses,
considered separately from the sep, shall not be considered as on the sheet of
assertion. Then, obviously, the antecedent and consequent must be in separate
compartments of the close. In order to make the representation of the relation
between them iconic, we must ask ourselves what spatial relation is analogous
to their relation. Now if it be true that "If a is true, b is true" and "If b
is true, c is true," then it is true that "If a is true, c is true." This is
analogous to the geometrical relation of inclusion. So naturally striking is
the analogy as to be (I believe) used in all languages to express the logical
relation; and even the modern mind, so dull about metaphors, employs this one
frequently. It is reasonable, therefore, that one of the two compartments
should be placed within the other. But which shall be made the inner one? Shall
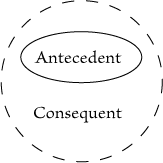
we express the conditional de inesse by Fig. 71 or by Fig. 72? In order to
decide which is the more appropriate mode of representation, one should observe
that the consequent of a conditional proposition asserts what is true, not
throughout the whole universe of possibilities considered, but in a subordinate
universe marked off by the antecedent. This is not a fanciful notion, but a
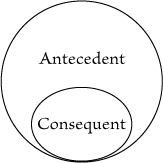
truth. Now in Fig. 72, the consequent appears in a special part of the sheet
representing the universe, the space between the two lines containing the
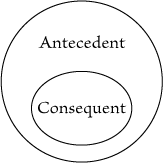
definition of the sub-universe.
|
| |
 |
 |
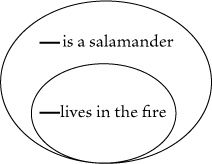
|
Figure 71(*1) |
Figure 72 |
|
| |
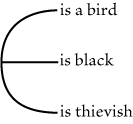
There is no such expressiveness in Fig. 71 -- or, if there be, it is only of a
superficial and fanciful sort. Moreover, the necessity of using two kinds of
enclosing lines -- a necessity which, we shall find, does not exist in Fig. 72
-- is a defect of Fig. 71; and when we come to consider the question of
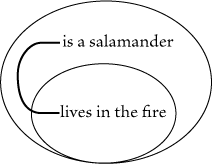
convenience, the superiority of Fig. 72 will appear still more strongly. This,
then, will be the method for us to adopt.
|
| |
|
|
| 436. |
The two seps
of Fig. 72, taken together, form a curve which I shall
call a scroll. The node is of no particular
significance. The scroll may equally well be drawn as in
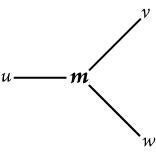
Fig. 73. |
| |
 |
|
Figure 73 |
|
| |
The only
essential feature is that there should be two seps, of which the inner, however drawn,
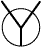
may be called the inloop. The node merely serves to aid the mind in the
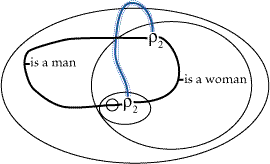
interpretation, and will be used only when it can have this effect. The two
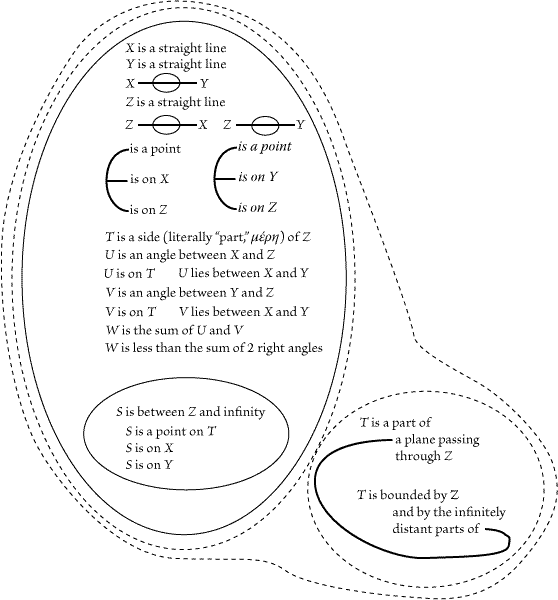
compartments will be called the inner, or second, close, and the
outer close,
the latter excluding the former. The outer close considered as containing the inloop will be called the
close. |
| |
|
|
| 437. |
Convention No. 3. An
enclosure shall be a graph consisting of a
scroll with its contents.
The scroll shall be a real curve of two closed branches, the one within
the other, called seps, and the inner specifically called the
loop; and these
branches may or may not be joined at a node.
The contents of the scroll shall consist of whatever is in the area
enclosed by the outer sep, this area being called the close and
consisting of the inner, or second,
close, which is the area enclosed by the loop,
and the outer, or first close,
which is the area outside the loop but inside the outer
sep.
When an enclosure is written on the sheet of assertion, although it is
asserted as a whole, its contents shall be cut off from the sheet, and shall
not be asserted in the assertion of the whole. But the enclosure shall assert
de inesse that if every graph in the outer close be true, then every graph in
the inner close is true. |
| |
|
|
| |
§3. OF CONVENTIONS NOS. 4 TO 9(*1P) |
|
438. |
Let a heavy dot or dash be used in place of a noun which has been
erased from a proposition. A blank form of proposition produced by such
erasures as can be filled, each with a proper name, to make a proposition
again, is called a rhema, or, relatively to the proposition of which it is
conceived to be a part, the predicate of that proposition. The following are
examples of rhemata: |
| |
 |
| |
Every proposition has one predicate and one only. But what that predicate is
considered to be depends upon how we choose to analyze it. Thus, the
proposition |
| |
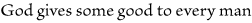 |
| |
may be considered as having for its predicate either of the following rhemata: |
| |
 |
| |
In the last case the entire proposition is considered as predicate. A rhema
which has one blank is called a monad; a rhema of two blanks, a dyad; a rhema
of three blanks, a triad; etc. A rhema with no blank is called a medad, and is
a complete proposition. A rhema of more than two blanks is a polyad. A rhema of
more than one blank is a relative. Every proposition has an ultimate predicate,
produced by putting a blank in every place where a blank can be placed, without
substituting for some word its definition. Were this done we should call it a
different proposition, as a matter of nomenclature. If on the other hand, we
transmute the proposition without making any difference as to what it leaves
unanalyzed, we say the expression only is different, as, if we say, |
| |
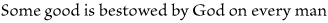 |
| |
Each part of a proposition which might be replaced by a proper name, and still
leave the proposition a proposition is a subject of the proposition.(*P1) It is,
however, the rhema which we have just now to attend to. |
| |
|
|
| 439. |
A rhema is, of course, not a proposition. Supposing, however, that
it be written on the sheet of assertion, so that we have to adopt a meaning for
it as a proposition, what can it most reasonably be taken to mean? Take, for
example, Fig. 74. Shall this, since it represents the universe, be taken to
mean that "Something in the universe is beautiful," or that "Anything in the
universe is beautiful," or that "The universe, as a whole, is beautiful"? The
last interpretation may be rejected at once for the reason that we are
generally unable to assert anything of the universe not reducible to one of the
other forms except what is well-understood between graphist and interpreter. We
have, therefore, to choose between interpreting Fig. 74 to mean "Something is
beautiful" |
| |
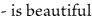 |
 |
|
Figure 74 |
Figure 75 |
|
| |
and to mean "Anything is beautiful." Each asserts the rhema of an individual;
but the former leaves that individual to be designated by the grapheus, while
the latter allows the rhema [interpreter q to fill the blank with any proper
name he likes. If Fig. 74 be taken to mean "Something is beautiful," then Fig.
75 will mean "Everything is beautiful"; while if Fig. 74 be taken to mean
"Everything is beautiful," then Fig. 75 will mean "Something is beautiful." In
either case, therefore, both propositions will be expressible, and the main
question is, which gives the most appropriate expressions? The question of
convenience is subordinate, as a general rule; but in this case the difference
is so vast in this respect as to give this consideration more than its usual
importance. |
| |
|
|
| 440. |
In order to decide the question of appropriateness, we must ask
which form of proposition, the universal or the particular, "Whatever
salamander there may be lives in fire," or "Some existing salamander lives in
fire," is more of the nature of a conditional proposition; for plainly, these
two propositions differ in form from "Everything is beautiful" and "Something
is beautiful" respectively, only in their being limited to a subsidiary
universe of salamanders. Now to say "Any salamander lives in fire" is merely to
say "If anything, X, is a salamander, X lives in fire." It differs from a
conditional, if at all, only in the identification of X which it involves. On
the other hand, there is nothing at all conditional in saying "There is a
salamander, and it lives in fire." Thus the interpretation of Fig. 74 to mean "Something is beautiful" is
decidedly the more appropriate; and since reasonable arrangements generally
prove to be the most convenient in the end, we shall not be surprised when we
come to find, as we shall, the same interpretation to be incomparably the
superior in that respect also.
|
| |
|
|
| 441. |
Convention No. 4. In this system, the unanalyzed expression of a rhema shall be called a
spot. A distinct place on its periphery shall be
appropriated to each blank, which place shall be called a hook. A spot with a
dot at each hook shall be a graph expressing the proposition which results from
filling every blank of the rhema with a separate sign of an indesignate
individual existing in the universe and belonging to some determinate category,
usually that of "things." |
| |
|
|
| 442. |
In many reasonings it becomes necessary to write a copulative
proposition in which two members relate to the same individual so as to
distinguish these members. Thus we have to write such a proposition as,
A is greater than something that is greater than B,
so as to exhibit the two partial graphs of Fig. 76. |
| |
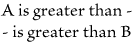 |
|
Figure 76 |
|
| |
The proposition we wish to express adds to those of Fig. 76 the assertion of
the identity of the two "somethings." But this addition cannot be effected as
in Fig. 77. |
| |
 |
|
Figure 77 |
|
| |
For the "somethings," being indesignate, cannot be described in general terms.
It is necessary that the signs of them should be connected in fact. No way of
doing this can be more perfectly iconic than that exemplified in Fig. 78. |
| |
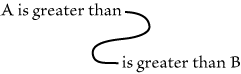 |
|
Figure 78 |
|
| |
Any sign of such identification of individuals may be called a
connexus, and the particular sign here used, which we shall do well to adopt,
may be called a line of identity. |
| |
|
|
| 443. |
Convention No. 5. Two coincident points, not more, shall denote
the same individual. |
| |
|
|
| 444. |
Convention
No. 6. A heavy line, called a line of identity,
shall be a graph asserting the numerical identity of the
individuals denoted by its two extremities. |
| |
|
|
| 445. |
The next
convention to be laid down is so perfectly natural that
the reader may well have a difficulty in perceiving that
a separate convention is required for it. Namely, we may
make a line of identity branch to express the identity
of three individuals. Thus, Fig. 79 |
| |
 |
|
Figure 79 |
|
| |
will express
that some black bird is thievish. No doubt, it would
have been easy to draw up Convention No. 4 in such a
form as to cover this procedure. But it is not our
object in this section to find ingenious modes of
statement which, being borne in mind, may serve as rules
for as many different acts as possible. On the contrary,
what we are here concerned to do is to distinguish all
proceedings that are essentially different. Now it is
plain that no number of mere bi-terminal bonds, each
terminal occupying a spot's hook, can ever assert the
identity of three things, although |
| |
 |
|
Figure 80 |
|
| |
when we once
have a three-way branch, any higher number of terminals
can be produced from it, as in Fig. 80. |
| |
|
|
| 446. |
We ought to, and must, then, make a distinct convention to cover
this procedure, as follows: Convention No. 7. A branching line of identity shall express a triad
rhema signifying the identity of the three individuals, whose designations are
represented as filling the blanks of the rhema by coincidence with the three
terminals of the line. |
| |
|
|
| 447. |
Remark how peculiar a sign the line of identity is. A sign, or, to
use a more general and more definite term, a representamen, is of one or other
of three kinds:(*1) it is either an icon, an index, or a symbol. An icon is a representamen of what it represents and for the mind that interprets it as
such, by virtue of its being an immediate image, that is to say by virtue of
characters which belong to it in itself as a sensible object, and which it
would possess just the same were there no object in nature that it resembled,
and though it never were interpreted as a sign. It is of the nature of an
appearance, and as such, strictly speaking, exists only in consciousness,
although for convenience in ordinary parlance and when extreme precision is not
called for, we extend the term icon to the outward objects which excite in
consciousness the image itself. A geometrical diagram is a good example of an
icon. A pure icon can convey no positive or factual information; for it affords
no assurance that there is any such thing in nature. But it is of the utmost
value for enabling its interpreter to study what would be the character of such
an object in case any such did exist. Geometry sufficiently illustrates that.
Of a completely opposite nature is the kind of representamen termed an index.
This is a real thing or fact which is a sign of its object by virtue of being
connected with it as a matter of fact and by also forcibly intruding upon the
mind, quite regardless of its being interpreted as a sign. It may simply serve
to identify its object and assure us of its existence and presence. But very
often the nature of the factual connexion of the index with its object is such
as to excite in consciousness an image of some features of the object, and in
that way affords evidence from which positive assurance as to truth of fact may
be drawn. A photograph, for example, not only excites an image, has an
appearance, but, owing to its optical connexion with the object, is evidence
that that appearance corresponds to a reality. A symbol is a representamen
whose special significance or fitness to represent just what it does represent
lies in nothing but the very fact of there being a habit, disposition, or other
effective general rule that it will be so interpreted. Take, for example, the
word "man." These three letters are not in the least like a man; nor is the
sound with which they are associated. Neither is the word existentially
connected with any man as an index. It cannot be so, since the word is not an
existence at all. The word does not consist of three films of ink. If the word
"man" occurs hundreds of times in a book of which myriads of copies are
printed, all those millions of triplets of patches of ink are embodiments of
one and the same word. I call each of those embodiments a replica of the
symbol. This shows that the word is not a thing. What is its nature? It
consists in the really working general rule that three such patches seen by a
person who knows English will effect his conduct and thoughts according to a
rule. Thus the mode of being of the symbol is different from that of the icon
and from that of the index. An icon has such being as belongs to past
experience. It exists only as an image in the mind. An index has the being of
present experience. The being of a symbol consists in the real fact that
something surely will be experienced if certain conditions be satisfied.
Namely, it will influence the thought and conduct of its interpreter. Every
word is a symbol. Every sentence is a symbol. Every book is a symbol. Every
representamen depending upon conventions is a symbol. Just as a photograph is an
index having an icon incorporated into it, that is,
excited in the mind by its force, so a symbol may have
an icon or an index incorporated into it, that is, the
active law that it is may require its interpretation to
involve the calling up of an image, or a composite
photograph of many images of past experiences, as
ordinary common nouns and verbs do; or it may require
its interpretation to refer to the actual surrounding
circumstances of the occasion of its embodiment, like
such words as that, this, I, you, which, here, now,
yonder, etc. Or it may be pure symbol, neither iconic
nor indicative, like the words and, or, of, etc. Peirce: |
| |
|
|
| 448. |
The value of an icon consists in its exhibiting the features of a
state of things regarded as if it were purely imaginary. The value of an index
is that it assures us of positive fact. The value of a symbol is that it serves
to make thought and conduct rational and enables us to predict the future. It
is frequently desirable that a representamen should exercise one of those three
functions to the exclusion of the other two, or two of them to the exclusion of
the third; but the most perfect of signs are those in which the iconic,
indicative, and symbolic characters are blended as equally as possible. Of this
sort of signs the line of identity is an interesting example. As a conventional
sign, it is a symbol; and the symbolic character, when present in a sign, is of
its nature predominant over the others. The line of identity is not, however,
arbitrarily conventional nor purely conventional. Consider any portion of it
taken arbitrarily (with certain possible exceptions shortly to be considered)
and it is an ordinary graph for which Fig. 81 might perfectly well be
substituted. But when we consider the |
| |
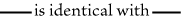 |
|
Figure 81 |
|
| |
connexion of this portion with a next adjacent portion, although the two
together make up the same graph, yet the identification of the something, to
which the hook of the one refers, with the something, to which the hook of the
other refers, is beyond the power of any graph to effect, since a graph, as a
symbol, is of the nature of a law, and is therefore general, while here there
must be an identification of individuals. This identification is effected not
by the pure symbol, but by its replica which is a thing. The termination of one
portion and the beginning of the next portion denote the same individual by
virtue of a factual connexion, and that the closest possible; for both are
points, and they are one and the same point. In this respect, therefore, the
line of identity is of the nature of an index. To be sure, this does not affect
the ordinary parts of a line of identity, but so soon as it is even conceived,
[it is conceived] as composed of two portions, and it is only the factual
junction of the replicas of these portions that makes them refer to the same
individual. The line of identity is, moreover, in the highest degree iconic.
For it appears as nothing but a continuum of dots, and the fact of the identity
of a thing, seen under two aspects, consists merely in the continuity of being
in passing from one apparition to another. Thus uniting, as the line of
identity does, the natures of symbol, index, and icon, it is fitted for playing
an extraordinary part in this system of representation. |
| |
|
|
| 449. |
There is no difficulty in interpreting the line of identity until
it crosses a sep. To interpret it in that case, two new conventions will be
required. How shall we express the proposition "Every salamander lives in fire,"
or "If it be true that something is a salamander then it will always be true
that that something lives in fire"? If we omit the assertion of the identity of
the somethings, the expression is obviously given in Fig. 82. |
| |
 |
|
Figure 82 |
|
| |
To that, we
wish to add the expression of individual identity. We
ought to use our line of identity for that. Then, we
must draw Fig. 83. |
| |
 |
|
Figure 83 |
|
| |
It would be unreasonable, after having adopted the line of identity as
our instrument for the expression of individual identity, to hesitate to employ
it in this case. Yet to regularize such a mode of expression two new
conventions are required. For, in the first place, we have not hitherto had any
such sign as a line of identity crossing a sep. This part of the line of
identity is not a graph; for a graph must be either outside or inside of each
sep.*1 In order, therefore, to legitimate our interpretation of Fig. 83, we
must agree that a line of identity crossing a sep simply asserts the identity
of the individual denoted by its outer part and the individual denoted by its
inner part. But this agreement does not of itself necessitate our
interpretation of Fig. 83; since this might be understood to mean, "There is
something which, if it be a salamander, lives in fire," instead of meaning, "If
there be anything that is a salamander, it lives in fire." But although the
last interpretation but one would involve itself in no positive contradiction,
it would annul the convention that a line of identity crossing a sep still
asserts the identity of its extremities -- not, indeed, by conflict with that
convention, but by rendering it nugatory. What does it mean to assert de inesse
that there is something, which if it be a salamander, lives in fire? It
asserts, no doubt, that there is something. Now suppose that anything lives in
fire. Then of that it will be true de inesse that if it be a salamander, it
lives in fire; so that the proposition will then be true. Suppose that there is
anything that is not a salamander. Then, of that it will be true de inesse that
if it be a salamander, it lives in fire; and again the proposition will be
true. It is only false in case whatever there may be is a salamander while
nothing lives in fire. Consequently, Fig. 83 would be precisely equivalent to
Fig. 84 [Click here to view], |
| |
 |
|
Figure 84 |
|
| |
and there
would be no need of any line of identity's crossing a
sep. It would then be impossible to express a universal
categorical analytically except by resorting to an unanalytic expression of
such a proposition or something substantially equivalent to that.(*P1)
Two conventions, then, are necessary. In stating them, it will be well
to avoid the idea of a graph's being cut through by a sep, and confine
ourselves to the effects of joining dots on the sep to dots outside and inside
of it.
|
| |
|
|
| 450. |
Convention No. 8. Points on a sep shall be considered to lie
outside the close of the sep so that the junction of such a point with any
other point outside the sep by a line of identity shall be interpreted as it
would be if the point on the sep were outside and away from the sep. |
| |
|
|
| 451. |
Convention No. 9. The junction by a line of identity of a point on
a sep to a point within the close of the sep shall assert of such individual as
is denoted by the point on the sep, according to the position of that point by
Convention No. 8, a hypothetical conditional identity, according to the
conventions applicable to graphs situated as is the portion of that line that
is in the close of the sep. |
| |
|
|
| 452. |
It will be well to illustrate these conventions by some examples.
Fig. 85 asserts that if it be true that something is good, then this assertion
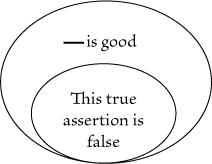
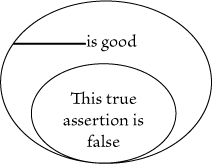
is false. That is, the assertion is that nothing is good. But in Fig. 86, the
terminal of the line of identity on the outer sep asserts that something, X,
exists, and it is only of this existing individual, X, that it is asserted that
if that is good the assertion is false. It therefore means |
| |
 |
 |
|
Figure
85 |
Figure
86 |
|
| |
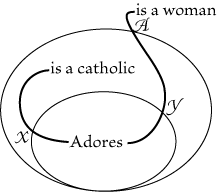
"Something is not good." On Fig. 87 and Fig. 88 the points on the seps are
marked with letters, for convenience of reference. Fig. 87 asserts that
something, A, is a woman; and that if there is an individual, X, that is a
catholic, and an individual, Y, that is identical with A, then X adores Y; that
is, some woman is adored by all catholics, if there are any. Fig. 88 asserts
that if there be an individual, X, and if X is a catholic, then X adores
somebody that is a woman. That is, whatever |
| |
 |
 |
|
Figure
87 |
Figure
88 |
|
| |
catholic there may be adores some woman or other. This does
not positively assert that any woman exists, but only that if
there is a catholic, then there is a woman whom he adores.
|
| |
|
|
| 453. |
A triad rhema gives twenty-six affirmative forms of
simple general propositions, as follows: |
| |
|
| |
For a tetrad there are 150 such forms; for a pentad 1082; for a hexad 9366;
etc. |
| |
|
|
| |
B. Derived Principles of InterpretationP |
| |
§1. OF THE PSEUDOGRAPH AND CONNECTED SIGNSP |
| 454. |
It is, as will soon appear, sometimes desirable to express a
proposition either absurd, contrary to the understanding between the graphist
and the interpreter, or at any rate well-known to be false. From any such
proposition, as antecedent, any proposition whatever follows as a consequent de
inesse. Hence, every such proposition may be regarded as implying that
everything is true; and consequently all such propositions are equivalent. The
expression of such a proposition may very well fill the entire close in which
it is, since nothing can be added to what it already implies. Hence we may
adopt the following secondary convention. Convention No. 10. The pseudograph, or expression in this system of a
proposition implying that every proposition is true, may be drawn as a black
spot entirely filling the close in which it is. |
| |
|
|
| 455. |
Since the size of signs has no significance, the blackened close
may be drawn invisibly small. Thus Fig. 97 [may be scribed] as in Fig. 98, or
even as in Fig. 99, Fig. 100, or lastly as in Fig. 101.(*1) |
| |
 |
 |
 |
 |
 |
|
Figure 97 |
Figure 98 |
Figure 99 |
Figure 100 |
Figure 101 |
|
| |
|
|
| 456. |
Interpretational Corollary 1. A scroll with its contents having
the pseudograph in the inner close is equivalent to the precise denial of the
contents of the outer close.
For the assertion, as in Fig. 97, that de inesse if a is true
everything is true, is equivalent to the assertion that a is not true, since if
the conditional proposition de inesse be true a cannot be true, and if a is not
true the conditional proposition de inesse, having a for its antecedent, is
true. Hence the one is always true or false with the other, and they are
equivalent.
This corollary affords additional justification for writing Fig. 97 as
in Fig. 101, since the effect of the loop enclosing the pseudograph is to make
a precise denial of the absurd proposition; and to deny the absurd is
equivalent to asserting nothing. |
| |
|
|
| 457. |
Interpretational Corollary 2. A disjunctive proposition may be
expressed by placing its members in as many inloops of one sep. But this will
not exclude the simultaneous truth of several members or of all.
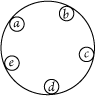
Thus, Fig. 102 will express that either
a or b or
c or d or e is true. For it will deny the simultaneous denial of all. |
| |
 |
|
Figure 102 |
|
| |
|
|
| 458. |
Interpretational Corollary 3. A graph may be interpreted by
copulations and disjunctions. Namely, if a graph within an odd number of seps
be said to be oddly enclosed, and a graph within no sep or an even number of seps be said to be
evenly enclosed, then spots in the same compartment are
copulated when evenly enclosed, and disjunctively combined when oddly enclosed;
and any line of identity whose outermost part is evenly enclosed refers to
something, and any one whose outermost part is oddly enclosed refers to
anything there may be. And the interpretation must begin outside of all seps
and proceed inward. And spots evenly enclosed are to be taken affirmatively;
those oddly enclosed negatively.
For example, Fig. 83 may be read, Anything whatever is either not a
salamander or lives in fire. Fig. 87 may be read, Something, A, is a woman, and
whatever X may be, either X is not a catholic or X adores A. Fig. 88 may be
read, Whatever X may be, either X is not a catholic or there is something Y,
such that X adores Y and Y is a woman. Fig. 96 may be read, Whatever A may be,
there is something C, such that whatever B may be, A blames B to C. Fig. 103
may be read, Whatever X and Y may be, either X is not a
saint or Y is not a saint or X loves Y; that is, Every
saint there may be loves every saint. So Fig. 104 |
| |
 |
 |
|
Figure 103 |
Figure 104 |
|
| |
may be read,
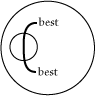
Whatever X and Y may be, either X is not best or Y is
not best or X is identical with Y; that is, there are
not two bests. Fig. 105 [Click here to view] may be
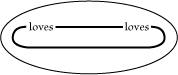
read, Whatever X and Y may be, either X does not love Y
or Y does not love X; that is, no two love each other.
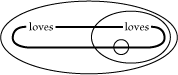
Fig. 106 [Click here to view] may be read, Whatever X
and Y may be either X does not love Y or there is
something L and X is not L but Y loves L; that is,
nobody loves anybody who does not love somebody else |
| |
 |
 |
|
Figure 105 |
Figure 106 |
|
| |
|
|
| 459. |
Interpretational Corollary 4. A sep which is vacant,
except for a line of identity traversing it, expresses
with its contents the non-identity of the extremities of
that line. |
| |
|
|
| |
§2. SELECTIVES AND PROPER NAMESP |
| 460. |
It is sometimes impossible upon an ordinary surface to draw a
graph so that lines of identity will not cross one another. If, for example, we
express that x is a value that can result from raising z to the power whose
exponent is y, by means of Fig. 107, and express that u is a value that can
result from multiplying w by v, by Fig. 108, then in order to express that |
| |
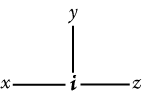 |
 |
|
Figure 107 |
Figure 108 |
|
| |
whatever values
x, y, and z may be, there is a value resulting from raising x
to a power whose exponent is a value of the product of z by y which same value
is also one of the values resulting from raising to the power z a value
resulting from raising x to the power y (this being one of the propositions
expressed by the equation x(yz) = (xy)z) we may draw Fig. 109 ; |
| |
|
| |
but there is an unavoidable intersection of two lines of identity. In
such a case, and indeed in any case in which the lines of identity become too
intricate to be perspicuous, it is advantageous to replace some of them by
signs of a sort that in this system are called selectives. A selective is very
much of the same nature as a proper name; for it denotes an individual and its
outermost occurrence denotes a wholly indesignate individual of a certain
category (generally a thing) existing in the universe, just as a proper name,
on the first occasion of hearing it, conveys no more. But, just as on any
subsequent hearing of a proper name, the hearer identifies it with that
individual concerning which he has some information, so all occurrences of the
selective other than the outermost must be understood to denote that identical
individual. If, however, the outermost occurrence of any given selective is
oddly enclosed, then, on that first occurrence the selective will refer to any
individual whom the interpreter may choose, and in all other occurrences to the
same individual. If there be no one outermost occurrence, then any one of those
that are outermost may be considered as the outermost. The later capital
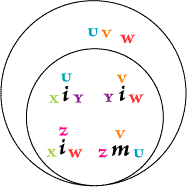
letters are used for selectives. For example, Fig. 109 is otherwise expressed
in Figs. 110 and 111. |
| |
 |
 |
|
Figure 110(z2) |
Figure 111 |
|
| |
Fig. 111 may
be read, "Either no value is designated as
U,
or no value is designated as V,
or no value is designated as W,
or else a value designated as
Y results from raising
W
to the V power, and a value
designated as Z
results from multiplying U
by V, and a value
designated as X results
from raising Y to the
U power, while this same value
X results from raising
W to the Z
power." |
| |
|
|
| 461. |
Convention No. 11. The capital letters of the alphabet shall be
used to denote single individuals of a well-understood category, the individual
existing in the universe, the early letters preferably as proper names of
well-known individuals, the later letters, called selectives, each on its first
occurrence, as the name of an individual (that is, an object existing in the
universe in a well-understood category; that is, having such a mode of being as
to be determinate in reference to every character as wholly possessing it or
else wholly wanting it), but an individual that is indesignate (that is, which
the interpreter receives no warrant for identifying); while in every occurrence
after the first, it shall denote that same individual. Of two occurrences of
the same selective, either one may be interpreted as the earlier, if and only
if, enclosed by no sep that does not enclose the other. A selective at its
first occurrence shall be asserted in the mode proper to the compartment in
which it occurs. If it be on that occurrence evenly enclosed, it is only
affirmed to exist under the same conditions under which any graph in the same
close is asserted; and it is then asserted, under those conditions, to be the
subject filling the rhema-blank corresponding to any hook against which it may
be placed. If, however, at its first occurrence, it be
oddly enclosed, then, in the disjunctive mode of
interpretation, it will be denied, subject to the
conditions proper to the close in which it occurs, so
that its existence being disjunctively denied, a
non-existence will be affirmed, and as a subject, it
will be universal (that is, freed from the
condition of wholly possessing or wholly wanting each
character) and at the same time designate (that is, the
interpreter will be warranted in identifying it with whatever the context may
allow), and it will be, subject to the conditions of the close, disjunctively
denied to be the subject filling the rhema-blank of the hook against which it
may be placed. In all subsequent occurrences it shall
denote the individual with which the interpreter may, on
its first occurrence, have identified it, and otherwise
will be interpreted as on its first occurrence. Resort must be had to the examples to trace out the sense of this long
abstract statement; and the line of identity will aid in explaining the
equivalent selectives. Fig. 112 may be read |
| |
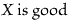 |
 |
|
Figure 112 |
Figure 113 |
|
| |
there exists
something that may be called X and it is good. Fig. 113,
the precise denial of Fig. 112, may be read "Either
there is not anything to be called X or whatever there
may be is not good," or "Anything you may choose to call
X is not good," or "all things are non-good." "Anything"
is not an individual subject, since the two
propositions, "Anything is good" and "Anything is bad,"
do not exhaust the possibilities. Both may be false. |
| |
|
|
| 462. |
Convention No. 12. The use of selectives may be avoided, where it
is desired to do so, by drawing parallels on both sides of the lines of
identity where they appear to cross.(*1) |
| |
|
|
| |
§3. OF ABSTRACTION AND ENTIA RATIONIS
(*1)P |
| 463. |
The term abstraction bears two utterly different meanings in
philosophy. In one sense it is applied to a psychological act by which, for
example, on seeing a theatre, one is led to call up images of other theatres
which blend into a sort of composite in which the special features of each are
obliterated. Such obliteration is called precisive abstraction. We shall have
nothing to do with abstraction in that sense. But when that fabled old doctor,
being asked why opium put people to sleep, answered that it was because opium
has a dormative virtue, he performed this act of immediate inference:
| |
Opium causes people to sleep; |
| Hence, |
Opium possesses a power of causing sleep |
The peculiarity of such inference is that the conclusion relates to something
-- in this case, a power -- that the premiss says nothing about; and yet the
conclusion is necessary. Abstraction, in the sense in which it will here be
used, is a necessary inference whose conclusion refers to a subject not
referred to by the premiss; or it may be used to denote the characteristic of
such inference. But how can it be that a conclusion should necessarily follow
from a premiss which does not assert the existence of that whose existence is
affirmed by it, the conclusion itself? The reply must be that the new
individual spoken of is an ens rationis; that is, its being consists in some
other fact. Whether or not an ens rationis can exist or be real, is a question
not to be answered until existence and reality have been very distinctly
defined. But it may be noticed at once, that to deny every mode of being to
anything whose being consists in some other fact would be to deny every mode of
being to tables and chairs, since the being of a table depends on the being of
the atoms of which it is composed, and not vice versa. |
| |
|
|
| 464. |
Every symbol is an
ens rationis, because it consists in a habit,
in a regularity; now every regularity consists in the future conditional
occurrence of facts not themselves that regularity. Many important truths are
expressed by propositions which relate directly to symbols or to ideal objects
of symbols, not to realities. If we say that two walls collide, we express a
real relation between them, meaning by a real relation one which involves the
existence of its correlates. If we say that a ball is red, we express a
positive quality of feeling really connected with the ball. But if we say that
the ball is not blue, we simply express -- as far as the direct expression goes
-- a relation of inapplicability between the predicate blue, and the ball or
the sign of it. So it is with every negation. Now it has already been shown
that every universal proposition involves a negation, at least when it is
expressed as an existential graph. On the other hand, almost every graph
expressing a proposition not universal has a line of identity. But identity,
though expressed by the line as a dyadic relation, is not a relation between
two things, but between two representamens of the same thing. |
| |
|
|
| 465. |
Every rhema whose blanks may be filled by signs of ordinary
individuals, but which signifies only what is true of symbols of those
individuals, without any reference to qualities of sense, is termed a rhema of
second intention. For second intention is thought about thought as symbol.
Second intentions and certain entia rationis demand the special attention of
the logician. Avicenna defined logic as the science of second intentions, and
was followed in this view by some of the most acute logicians, such as Raymund
Lully, Duns Scotus, Walter Burleigh, and Armandus de Bello Visu; while the
celebrated Durandus ā Sancto Porciano, followed by Gratiadeus Esculanus, made
it relate exclusively to entia rationis, and quite rightly. |
| |
|
|
| 466. |
Interpretational Corollary 5. A blank, considered as a medad,
expresses what is well-understood between graphist and interpreter to be true;
considered as a monad, it expresses "_ exists" or "_
is true"; considered as a
dyad, it expresses " _ coexists with
_" or "and." |
| |
|
|
| 467. |
Interpretational Corollary 6. An empty sep with its surrounding
blank, as in Fig. 114, is the pseudograph. Whether it be taken as medad, monad,
or dyad, for which purpose it will be written as in Figs. 115, 116, it is the
denial of the blank. |
| |
 |
 |
 |
|
Figure 114 |
Figure 115 |
Figure 116 |
|
| |
|
|
| 468. |
Interpretational Corollary 7. A line of identity traversing a sep
will signify non-identity. Thus Fig. 117 will express that
there are at least two men. |
| |
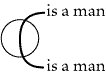 |
|
Figure 117 |
|
| |
|
|
| 469. |
Interpretational Corollary 8. A branching of a line of identity
enclosed in a sep, as in Fig. 118, will express that three
individuals are not all identical. |
| |
 |
|
Figure 118 |
|
| |
We now come to another kind of graphs which may go under the general
head of second intentional graphs.(*1)
|
| |
|
|
| 470. |
Convention No. 13. The letters,
r0
r1,
r2,
r3,
etc., each
with a number of hooks greater by one than the subscript number, may be taken
as rhemata, signifying that the individuals joined to the hooks, other than the
one vertically above the {r}, taken in their order clockwise, are capable of
being asserted of the rhema indicated by the line of identity joined vertically
to the r. |
| |
 |
|
Figure 119 |
|
| |
Thus, Fig. 119 expresses that there is a relation
in which every man stands to some woman to whom no other man stands in the same
relation; that is, there is a woman corresponding to every man or, in other
words, there are at least as many women as men. The dotted lines, between
which, in Fig. 119, the line of identity denoting the ens rationis is
placed, are by no means necessary. |
| |
|
|
| 471. |
Convention No. 14. The line of identity representing an
ens
rationis may be placed between two rows of dots, or it may be drawn in ink of
another colour, and any graph, which is to be spoken of as a thing, may be
enclosed in a dotted oval with a dotted line attached to it. Other entia
rationis may be treated in the same way, the patterns of the dotting being
varied for those of different category.
The graph of Fig. 120 is an example. It may be
read, as follows: "Euclid *2 enunciates it as a postulate that if two straight
lines are cut by a third straight line so that those angles the two make with
the third, these angles lying between the first two lines(τας
έντος γωνιας) and on the same side of the third, are less than two right angles, then that
those two lines shall meet on that same side; and in this enunciation, by a
side, μέρη, of the third line must be understood part of a plane that contains
that third line, which part is bounded by that line and by the infinitely
distant parts of the plane." . . . |
| |
 |
|
Figure 120 |
|
| |
|
|
| |
C. RecapitulationP |
| 472. |
The principles of interpretation may now be restated more
concisely and more comprehensibly. In this resume, it will be assumed that selectives, which should be regarded as a mere abbreviating device, and which
constitute a serious exception to the general idea of the system, are not used.
A person, learning to use the system and not yet thoroughly expert in it, might
be led to doubt whether every proposition is capable of being expressed without
selectives. For a line of identity cannot identify two individuals within
enclosures outside of one another without passing out of both enclosures, while
a selective is not subject to that restriction. It can be shown, however, that
this restriction is of no importance nor even helps to render thought clear.
Suppose then that two designations of individuals are to be identified, each
being within a separate nest of seps, and the two nests being within a common
nest of outer seps. The question is whether this identification can always be
properly effected by a line of identity that passes out of the two separate
nests of seps, and if desired, still farther out. The answer is plain enough
when we consider that, having to say something of individuals, some to be named
by the grapheus, others by the graphist, we can perfectly well postpone what we
have to say until all these individuals are indicated; that is to say, the
order in which they are to be specified by one and the other party. But if this
be done, these individuals will first appear, even if selectives are used, in
one nest of seps entirely outside of all the spots; and then these selectives
can be replaced by lines of identity. |
| |
|
|
| 473. |
The respect in which selectives violate the general idea of the
system is this; the outermost occurrence of each selective has a different
significative force from every other occurrence -- a grave fault, if it be
avoidable, in any system of regular and exact representation. The consequence
is that the meaning of a partial graph containing a selective depends upon
whether or not there be another part, which may be written on a remote part of
the sheet in which the same selective occurs farther out. But the idea of this
system is that assertions written upon different parts of the sheet should be
independent of one another, if, and only if, they have no common part. When
lines of identity are used to the exclusion of selectives, no such
inconvenience can occur, because each line of one partial graph will retain
precisely the same significative force, no matter what part outside of it be
removed (though if a line be broken, the identity of the individuals denoted by
its two parts will no longer be affirmed); and even if everything outside a sep
be removed (the sep being unbreakable by any removal of a partial graph, or
part which written alone would express a proposition) still there remains a
point on the sep which retains the same force as if the line had been broken
quite outside and away from the sep. |
| |
|
|
| 474. |
Rejecting the selectives, then, the principles of interpretation
reduce themselves to simple form, as follows:
- The writing of a proposition on the sheet of assertion unenclosed is
to be understood as asserting that proposition; and that, independently of any other
proposition on the sheet, except so far as the two
may have some part or point in common.
- A "spot," or unanalyzed
expression of a rhema, upon this system, has upon
its periphery a place called a "hook" appropriated
to every blank of the rhema; and whenever it is
written a heavily marked point occupies each hook.
Now every heavily marked point, whether isolated or
forming a part of a heavy line, denotes an denotes an indesignate individual, and being unenclosed affirms the
existence of some such individual; and if it occupy a hook of a spot it is the
corresponding subject of the rhema signified by the spot. A heavy line is to be
understood as asserting, when unenclosed, that all its points denote the same
individual, so that any portion of it may be regarded as a spot.
- A sep, or lightly drawn oval, when unenclosed is
with its contents (the whole being called an
enclosure) a graph, entire or partial, which
precisely denies the proposition which the entire
graph within it would, if unenclosed, affirm. Since,
therefore, an entire graph, by the above principles,
copulatively asserts all the partial graphs of which
it is composed, and takes every indesignate individual, denoted by a heavily marked point that may be a
part of it, in the sense of "something," it follows that an unenclosed
enclosure disjunctively denies all the partial graphs which compose the
contents of its sep, and takes every heavily marked point included therein in
the sense of "anything" whatever. Consequently, if an enclosure is oddly
enclosed, its evenly enclosed contents are copulatively affirmed; while if it
be evenly enclosed, its oddly enclosed contents are disjunctively denied.
- A heavily marked point upon a sep, or line of enclosure, is to be
regarded as no more enclosed than any point just outside of and away from the
sep, and is to be interpreted accordingly. But the effect of joining a heavily
marked point within a sep to such a point upon the sep itself by means of a
heavy line is to limit the disjunctive denial of existence (which is the effect
of the sep upon the point within it) to the individual denoted by the point
upon the sep. No heavy line is to be regarded as cutting a sep; nor can any
graph be partly within a sep and partly outside of it; although the entire
enclosure (which is not inside the sep) may be part of a graph outside of the
sep.(*1)
- A dotted oval is sometimes used to show that that which is within it
is to be regarded as an ens rationis.
|
| |
|
|
| |
PART II. THE PRINCIPLES OF ILLATIVE TRANSFORMATIONP |
| |
A. Basic PrinciplesP |
| |
§1. SOME AND ANY |
| 475. |
The first part of this tract was a grammar of this language of
graphs. But one has not mastered a language as long as one has to think about
it in another language. One must learn to think in it about facts. The present
part is designed to show how to reason in this language without translating it
into another, the language of our ordinary thought. This reasoning, however,
depends on certain first principles, for the justification of which we have to
make a last appeal to instinctive thought. |
| |
|
|
| 476. |
The purpose of reasoning is to proceed from the recognition of the
truth we already know to the knowledge of novel truth. This we may do by
instinct or by a habit of which we are hardly conscious. But the operation is
not worthy to be called reasoning unless it be deliberate, critical,
self-controlled. In such genuine reasoning we are always conscious of
proceeding according to a general rule which we approve. It may not be
precisely formulated, but still we do think that all reasoning of that perhaps
rather vaguely characterized kind will be safe. This is a doctrine of logic. We
never can really reason without entertaining a logical theory. That is called
our logica utens.(*1) |
| |
|
|
| 477. |
The purpose of logic is attained by any single passage from a premiss to a conclusion, as long as it does not at once happen that the premiss
is true while the conclusion is false. But reasoning proceeds upon a rule, and
an inference is not necessary, unless the rule be such that in every case the
fact stated in the premiss and the fact stated in the conclusion are so related
that either the premiss will be false or the conclusion will be true. (Or both,
of course. "Either A or B" does not properly exclude "both A and B.") Even
then, the reasoning may not be logical, because the rule may involve matter of
fact, so that the reasoner cannot have sufficient ground to be absolutely
certain that it will not sometimes fail. The inference is only logical if the
reasoner can be mathematically certain of the excellence of his rule of
reasoning; and in the case of necessary reasoning he must be mathematically
certain that in every state of things whatsoever, whether now or a million
years hence, whether here or in the farthest fixed star, such a premiss and
such a conclusion will never be, the former true and the latter false. It would
be far beyond the scope of this tract to enter upon any thorough discussion of
how this can be. Yet there are some questions which concern us here -- as, for
example, how far the system of rules of this section is eternal verity, and how
far it merely characterizes the special language of existential graphs -- and
yet trench closely upon the deeper philosophy of logic; so that a few remarks
meant to illuminate those pertinent questions and to show how they are
connected with the philosophy of logic seem to be quite in order. |
| |
|
|
| 478. |
Mathematical certainty is not absolute certainty. For the greatest
mathematicians sometimes blunder, and therefore it is possible -- barely
possible -- that all have blundered every time they added two and two. Bearing
in mind that fact, and bearing in mind the fact that mathematics deals with
imaginary states of things upon which experiments can be enormously multiplied
at very small cost, we see that it is not impossible that inductive processes
should afford the basis of mathematical certainty; and any mathematician can
find much in the history of his own thought, and in the public history of
mathematics to show that, as a matter of fact, inductive reasoning is
considerably employed in making sure of the first mathematical premisses.
Still, a doubt will arise as to whether this is anything more than a
psychological need, whether the reasoning really rests upon induction at all. A
geometer, for example, may ask himself whether two straight lines can enclose
an area of their plane. When this question is first put, it is put in reference
to a concrete image of a plane; and, at first, some experiments will be tried
in the imagination. Some minds will be satisfied with that degree of certainty:
more critical intellects will not. They will reflect that a closed area is an
area shut off from other parts of the plane by a boundary all round it. Such a
thinker will no longer think of a closed area by a composite photograph of
triangles, quadrilaterals, circles, etc. He will think of a predictive rule --
a thought of what experience one would intend to produce who should intend to
establish a closed area. |
| |
|
|
| 479. |
That step of thought, which consists in interpreting an image by a
symbol, is one of which logic neither need nor can give any account, since it
is subconscious, uncontrollable, and not subject to criticism. Whatever account
there is to be given of it is the psychologist's affair. But it is evident that
the image must be connected in some way with a symbol if any proposition is to
be true of it. The very truth of things must be in some measure representative. |
| |
|
|
| 480. |
If we admit
that propositions express the very reality, it is not
surprising that the study of the nature of propositions
should enable us to pass from the knowledge of one fact
to the knowledge of another.(*P1)
|
| |
|
|
| 481. |
We frame a system of expressing propositions -- a written language
-- having a syntax to which there are absolutely no exceptions. We then satisfy
ourselves that whenever a proposition having a certain syntactical form is
true, another proposition definitely related to it -- so that the relation can
be defined in terms of the appearance of the two propositions on paper -- will
necessarily also be true. We draw up our code of basic rules of such illative
transformations, none of these rules being a necessary consequence of others.
We then proceed to express in our language the premisses of long and difficult
mathematical demonstrations and try whether our rules will bring out their
conclusions. If, in any case, not, and yet the demonstration appears sound, we
have a lesson in logic to learn. Some basic rule has been omitted, or else our
system of expression is insufficient. But after our system and its rules are
perfected, we shall find that such analyses of demonstrations teach us much
about those reasonings. They will show that certain hypotheses are superfluous,
that others have been virtually taken for granted
without being expressly. laid down; and they will show
that special branches of mathematics are characterized
by appropriate modes of reasoning, the knowledge of
which will be useful in advancing them. We may now lay
all that aside, and begin again, constructing an
entirely different system of expression, developing it
from an entirely different initial idea, and having
perfected it, as we perfected the former system, we
shall analyze the same mathematical demonstrations. The
results of the two methods will agree as to what is and
what is not a necessary consequence. But a consequence
that either method will represent as an immediate
application of a basic rule, and therefore as simple,
the other will be pretty sure to analyze into a series
of steps. If it be not so, in regard to some inference
the one method will be merely a disguise of the other.
To say that one thing is simpler than another is an
incomplete proposition, like saying that one ball is to
the right of another. It is necessary to specify what
point of view is assumed, in order to render the
sentence true or false. |
| |
|
|
| 482. |
This remark has its application to the business now in hand, which
is to translate the effect of each simple illative transformation of an
existential graph into the language of ordinary thought and thus show that it
represents a necessary consequence. For it will be found that it is not the
operations which are simplest in this system that are simplest from the point
of view of ordinary thought; so that it will be found that the simplest way to
establish by ordinary thought the correctness of our basic rules will be to
begin by proving the legitimacy of certain operations that are less simple from
the point of view of the existential graphs. |
| |
|
|
| 483. |
The first proposition for assent to which I shall appeal to
ordinary reason is this; when a proposition contains a number of anys and
somes, or their equivalents, it is a delicate matter to alter the form of
statement while preserving the exact meaning. Every some, as we have seen,(*1)
means that under stated conditions, an individual could be specified of which
that which is predicated of the some is [true], while every any means that what
is predicated is true of no matter what [specified] individual; and the
specifications of individuals must be made in a certain order, or the meaning
of the proposition will be changed. Consider, for example, the following
proposition: "A certain bookseller only quotes a line of poetry in case it was
written by some blind authoress, and he either is trying to sell any books she
may have written to the person to whom he quotes the line or else intends to
reprint some book of hers." Here the existence of a bookseller is categorically
affirmed; but the existence of a blind authoress is only affirmed conditionally
on that bookseller's quoting a line of poetry. As for any book by her, none
such is positively said to exist, unless the bookseller is not endeavoring to
sell all the books there may be by her to the person to whom he
quotes the line.
|
| |
|
|
| 484. |
Now the point to which I demand the assent of reason is that all
those individuals, whose selection is so referred to, might be named to begin
with, thus: "There is a certain individual, A, and no matter what Z and Y may
be, an individual, B, can be found such that whatever X may be, there is
something C, and A is a bookseller and if he quotes Z to Y, and if Z is a line
of poetry and Y is a person, then B is a blind poetess who has written Z, and
either X is not a book published by B or A tries to sell X to Y or else C is a
book published by B and A intends to reprint C." This is the precise equivalent
of the original proposition, and any proposition involving somes and anys, or
their equivalents, might equally be expressed by first thus defining exactly
what these somes and anys mean, and then going on to predicate concerning them
whatever is to be predicated. This is so evident that any proof of it would
only confuse the mind; and anybody who could follow the proof will easily see
how the proof could be constructed. But after the somes and anys have thus been
replaced by letters, denoting each one individual, the subsequent statement
concerns merely a set of designate individuals. |
| |
|
|
| |
§2. RULES FOR DINECTED GRAPHS |
| 485. |
In order, then, to make evident to ordinary reason what are the
simple illative transformations of graphs, I propose to imagine the lines of
identity to be all replaced by selectives, whose first occurrences are entirely
outside the substance of the graph in a nest of seps, where each selective
occurs once only and with nothing but existence predicated of it (affirmatively
or negatively according as it is evenly or oddly enclosed). I will then show
that upon such a graph certain transformations are permissible, and then will
suppose the selectives to be replaced by lines of identity again. We shall thus
have established the permissibility of certain transformations without the
intervention of selectives. |
| |
|
|
| 486. |
There will therefore be two branches to our inquiry. First, what
transformations may be made in the inner part of the graph where all the selectives have proper names, and secondly what transformations may be made in
the outer part where each selective occurs but once. It will be found that the
second inquiry almost answers itself after the first has been investigated, and
further, that the first class of transformations are precisely the same as if
all the first occurrences of selectives were erased and the others were
regarded as proper names. We therefore begin by inquiring what transformations
are permissible in a graph which has no connexi at all, neither lines of
identity nor selectives. |
| |
|
|
| 487. |
First of all, let us inquire what are those modes of illative
transformation by each of which any graph whatever, standing alone on the sheet
of assertion, may be transformed, and, at the same time, what are those modes
of illative transformation from each of which any graph whatever, standing
alone on the sheet of assertion, might result. Let us confine ourselves, in the
first instance, to transformations not only involving no connexi, but also
involving no entia rationis nor seps. Let us suppose a graph, say that of Fig.
121, |
| |
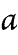 |
|
Figure 121 |
|
| |
to be alone upon the sheet of assertion. In what ways can it be illatively
transformed without using connexi nor seps nor other entia rationis? In the
first place, it may be erased; for the result of erasure, asserting nothing at
all, can assert nothing false. In the second place, it can be iterated, as in
Fig. 122; |
| |
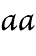 |
|
Figure 122 |
|
| |
for the result
of the iteration asserts nothing not asserted already.
In the third place, any graph, well-understood (before
the original graph was drawn) to be true, can be
inserted, as in The Fig. 123. |
| |
 |
|
Figure 123 |
|
| |
Evidently, these are the only modes of transformation
that conform to the assumed conditions. Next, let us
inquire in what manner any graph, say that of Fig. 124, |
| |
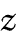 |
|
Figure 124 |
|
| |
can result. It cannot, unless of a special nature, result from insertion, since
the blank is true and the graph may be false; but it can result by any
omission, say of y from the graph of Fig. 125, |
| |
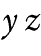 |
|
Figure 125 |
|
| |
whether y be true or false, or whatever its relation to
z, since the result
asserts nothing not asserted in the graph from which it results. |
| |
|
|
| 488. |
We may now employ the following:
Conditional Principle No. 1. If any graph, a, were it written alone on
the sheet of assertion, would be illatively transformable into another graph,
z, then if the former graph, a, is a partial graph of an entire graph involving
no connexus or sep, and written on the sheet of assertion, a may still be
illatively transformed in the same way.
For let a be a partial graph of which the other part is
m, in Fig. 126. |
| |
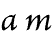 |
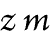 |
|
Figure 126 |
Figure 127 |
|
| |
Then, both a and
m will be asserted. But since a would be illatively
transformable into z if it were the entire graph, it follows that if a is true
z is true. Hence, the result of the transformation asserts only
m which is
already asserted, and z which is true if a, which is already asserted, is true. |
| |
|
|
| 489. |
By means of this principle we can evidently deduce the following:
Categorical Basic Rules for the Illative Transformation of Graphs
dinectively built up from partial graphs not separated by seps.
- Any partial graph may be erased.
- Any partial graph may be iterated.
- Any graph well-understood to be true may be
inserted.
It is furthermore clear that no transformation of such graphs is
logical, that is, results from the mere form of the graph, that is not
justified by these rules. For a transformation not justified by these rules
must insert something not in the premiss and not well-understood to be true.
But under those circumstances, it may be false, as far as appears from the
form. |
| |
|
|
| 490. |
Let us now consider graphs having no connexi or entia rationis
other than seps. Here we shall have the following
Conditional Principle No. 2. If a graph, a, were it written alone on
the sheet of assertion, would be illatively transformable into a sep containing
nothing but a graph, z, then in case nothing is on the sheet of assertion
except this latter graph, z, this will be illatively transformable into a sep
containing nothing but a. For to say that Fig. 123 [?121] is illatively transformable into Fig.
128, is to say that if a is true, then if z were true, anything you like would
be true; while to say that Fig. 124 is illatively transformable into Fig. 129
is to say that if z is true, then if a were true, anything you like would be
true. But each of these amounts to saying that if a and z were both true
anything you like would be true. Therefore, if either [transformation] is true
so is the other. |
| |
|
|
| 491. |
Conditional Principle No. 3. If a sep containing nothing but a
graph, a, would, were it written alone on the sheet of assertion, be illatively
transformable into a graph, z, then if a sep, containing nothing but the latter
graph, z, were written alone on the sheet of assertion, [this would] be
illatively transformable into the graph, a. |
| |
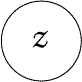 |
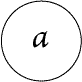 |
|
Figure 128 |
Figure 129 |
|
| |
For to say that Fig. 129 is illatively transformable into Fig. 124 is
to say that by virtue of the forms of a and z, if a is false, z is true; in
other words, by virtue of their forms, either a or z is true. But this is
precisely the meaning of saying that Fig. 128 is illatively transformable into
Fig. 123 [?121]. |
| |
|
|
| 492. |
By means of these principles we can deduce the following:
Basic Categorical Rules for the Illative Transformation of Graphs
dinectively built up from Partial Graphs and from Graphs separated by seps.
Rule 1. Within an even finite number (including none) of seps, any
graph may be erased; within an odd number any graph may be inserted.
Rule 2. Any graph may be iterated within the same or additional seps,
or if iterated, a replica may be erased, if the erasure leaves another outside
the same or additional seps.
Rule 3. Any graph well-understood to be true (and therefore an
enclosure having a pseudograph within an odd number of its seps) may be
inserted outside all seps.
Rule 4. Two seps, the one enclosing the
other but nothing outside that other, can be
removed.
|
| |
|
|
| 493. |
These rules have now to be demonstrated. The former set of rules,
already demonstrated, apply to every graph on the sheet of assertion composed
of dinected partial graphs not enclosed; for the reasoning of the
demonstrations so apply. It is now necessary to demonstrate, from Conditional
Principle No. 2, the following Principle of Contraposition: If any graph, say
that of Fig. 123 [?121], is illatively transformable into another graph, say
that of Fig. 124, then an enclosure consisting of a sep containing nothing but
the latter graph, as in Fig. 130, is illatively transformable into |
| |
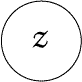 |
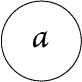 |
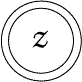 |
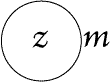 |
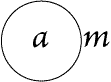 |
|
Figure 130 |
Figure 131 |
Figure 132 |
Figure 133 |
Figure 134 |
|
| |
an enclosure consisting of a sep containing nothing but the first graph, as in
Fig. 131. In order to prove this principle, we must first prove that any graph
on the sheet of assertion is illatively transformable by having two seps drawn
round it, the one containing nothing but the other with its contents. For let z
be the original graph. Then, it has to be shown that Fig. 124 is transformable
into Fig. 132. Now Fig. 130 on the sheet of assertion is illatively
transformable into itself since any graph is illatively transformable into any
graph that by virtue of its form cannot be false unless the original graph be
false, and Fig. 130 cannot be false unless Fig. 130 is false. But from this it
follows, by Conditional Principle No. 2, that Fig. 124 is illatively
transformable into Fig. 132. Q. E. D. The principle of contraposition, which
can now be proved without further difficulty, is that if any graph, a, (Fig.
123[?121], is illatively transformable into any graph, z, (Fig. 124) then an
enclosure (Fig. 130) consisting of a sep enclosing nothing but the latter
graph, z, is transformable into an enclosure (Fig. 131) consisting of a sep
containing nothing but the first graph, a. If a is transformable into z, then,
by the rule just proved, it is transformable into Fig. 132, consisting of z
doubly enclosed with nothing between the seps. But if Fig. 123 [?121] is
illatively transformable into Fig. 132, then, by Conditional Principle No. 2,
Fig. 130 is illatively transformable into Fig. 131, Q. E. D. |
| |
|
|
| 494. |
Supposing, now, that Rule 1 holds good for any insertion or
omission within not more than any finite number, N, of seps, it will also hold
good for every insertion or omission within not more than N+1 seps. For in any
graph on the sheet of insertions of which a partial graph is an enclosure
consisting of a sep containing only a graph, z, involving a nest of N seps, let
the partial graph outside this enclosure be m, so that Fig. 133 is the entire
graph. Then application of the rule within the N+1 seps will transform z into
another graph, say a, so that Fig. 134 will be the result. Then a, were it
written on the sheet of assertion unenclosed and alone, would be illatively
transformable into z, since the rule is supposed to be valid for an insertion
or omission within N seps. Hence, by the principle of contraposition, Fig. 130
will be transformable into Fig. 131, and by Conditional Principle No. 1, Fig.
133 will be transformable into Fig. 134. It is therefore proved that if Rule 1
is valid within any number of seps up to any finite number, it is valid for the
next larger whole number of seps. But by Rule 1 of the former set of rules, it
is valid for N = 0, and hence it follows that it is valid within seps whose
number can be reached from 0 by successive additions of unity; that is, for any
finite number. Rule 1 is, therefore, valid as stated. It will be remarked that
the partial graphs may have any multitude whatsoever; but the seps of a nest
are restricted to a finite multitude, so far as this rule is concerned. A graph
with an endless nest of seps is essentially of doubtful meaning, except in
special cases. Thus Fig. 135, |
| |
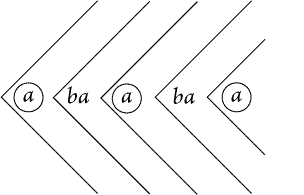 |
|
Figure 135 |
|
| |
supposed to
continue the alternation endlessly, evidently merely
asserts the truth of
a.(*1) But
if instead of ba, b were everywhere to stand alone, the graph would certainly
assert either a or b to be true and would certainly be true if a were true, but
whether it would be true or false in case b were true and not a is essentially
doubtful. |
| |
|
|
| 495. |
Rule 2 is so obviously demonstrable in the same way that it will
be sufficient to remark that unenclosed iterations of unenclosed graphs are
justified by Rule 2 of the former set of rules. Then, since Fig. 136 is
illatively transformable into |
| |
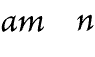 |
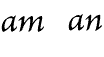 |
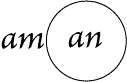 |
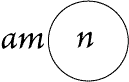 |
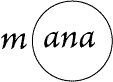 |
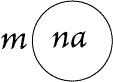 |
|
Figure 136 |
Figure 137 |
Figure 138 |
Figure 139 |
Figure 140 |
Figure 141 |
|
|
| |
Fig. 137, it follows from the principle of contraposition that Fig. 138 is
illatively transformable into Fig. 139. Or we may reason that to say that Fig.
137 follows from Fig. 136 is to say that, am being true, an follows from
n;
while to say that Fig. 139 follows from Fig. 138, is to say that, am being
true, as before, if from an anything you like follows, then from n anything you
like follows. In the same way Fig. 140 is transformable into Fig. 141. |
| |
|
|
| 496. |
The transformations the reverse of these, that is of Fig. 137 into
Fig. 136, of Fig. 139 into Fig. 138, and of Fig. 141 into Fig. 140 are
permitted by Rule 1. Then by the same Fermatian reasoning by which Rule 1 was
demonstrated, we easily show that a graph can anywhere be illatively inserted
or omitted, if there is another occurrence of the same graph in the same
compartment or farther out by one sep. For if Fig. 138 is transformable into
Fig. 139, then by the principle of contraposition, Fig. 142 is transformable
into Fig. 143, and by Conditional Principle No. 1, Fig. 144 is transformable in
Fig. 145. Having thus proved that iterations and deiterations are always
permissible in the same compartment as the leading replica or in a compartment
within one additional sep, we have no difficulty in extending this to any
finite interval. |
| |
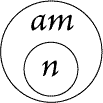 |
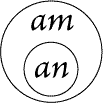 |
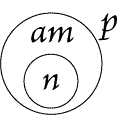 |
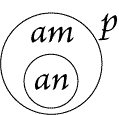 |
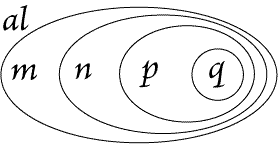 |
|
Figure 142 |
Figure 143 |
Figure 144 |
Figure 145 |
Figure 146 |
|
| |
Thus, Fig. 146 is transformable into Fig. 147, this into Fig. 148, this
successively into Figs. 149 to 153. Thus, the second rule is fully
demonstrable. Rule 3 is self-evident. |
| |
|
|
| 497. |
We have thus far had no occasion to appeal to Conditional
Principle No. 3; but it is indispensable for the proof of Rule 4. We have to
show that if any graph, which [we] may denote by z is surrounded by two seps
with nothing |
| |
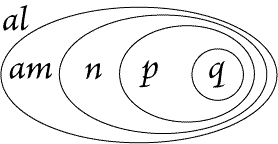 |
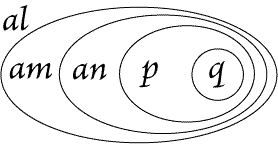 |
|
Figure 147 |
Figure 148 |
|
| |
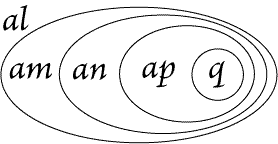 |
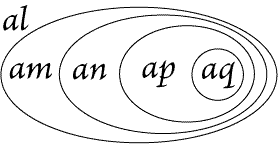 |
|
Figure 149 |
Figure 150 |
|
| |
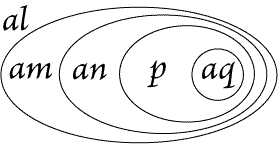 |
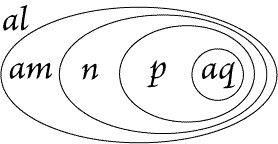 |
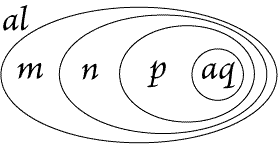 |
|
Figure 151 |
Figure 152 |
Figure 153 |
|
| |
between as in Fig. 132, then the two seps may be illatively removed as in Fig.
124. Now if the graph, z, occurred within one sep, as in Fig. 130, this, as we
have seen, would be transformed into itself. Hence, by Conditional Principle
No. 3, Fig. 132, can be illatively transformed into Fig. 124. Q. E. D. |
| |
|
|
| 498. |
The list of rules given for dinected graphs is complete. This is
susceptible of proof; but the proof belongs in the next section of this
chapter, where I may perhaps insert it. It is not interesting. |
| |
|
|
| |
B. Rules for Lines of Identity |
| 499. |
We now pass to the consideration of graphs connected by lines of
identity. A small addition to our nomenclature is required here. Namely, we
have seen that a line of identity is a partial graph; and as a graph it cannot
cross a sep. Let us, then, call a series of lines of identity abutting upon one
another at seps, a ligature; and we may extend the meaning of the word so that
even a single line of identity shall be called a ligature. A ligature composed
of more than one line of identity may be distinguished as a compound ligature.
A compound ligature is not a graph, because by a graph we mean something which,
written or drawn alone on the sheet of assertion, would, according to this
system, assert something. Now a compound ligature could not be written alone on
the sheet of assertion, since it is only by means of the intercepting sep,
which is no part of it, that it is rendered compound. The different spots, as
well as the different hooks, upon which a ligature abuts, may be said to be
ligated by that ligature; and two replicas of the same graph are said to have
the same ligations only when all the corresponding hooks of the two are ligated
to one another. When a ligature cuts a sep, the part of the ligature outside
the sep may be said to be extended to the point of intersection on the sep,
while the part of the ligature inside may be said to be joined to that point. |
| |
|
|
| 500. |
It has already(*1) been pointed out that the mass of ink on the
sheet by means of which a graph is said to be "scribed" is not, strictly
speaking, a symbol, but only a replica of a symbol of the nature of an index.
Let it not be forgotten that the significative value of a symbol consists in a
regularity of association, so that the identity of the symbol lies in this
regularity, while the significative force of an index consists in an
existential fact which connects it with its object, so that the identity of the
index consists in an existential fact or thing. When symbols, such as words,
are used to construct an assertion, this assertion relates to something real.
It must not only profess to do so, but must really do so; otherwise, it could
not be true; and still less, false. Let a witness take oath, with every legal
formality, that John Doe has committed murder, and still he has made no
assertion unless the name John Doe denotes some existing person. But in order
that the name should do this, something more than an association of ideas is
requisite. For the person is not a conception but an existent thing. The name,
or rather, occurrences of the name, must be existentially connected with the
existent person. Therefore, no assertion can be constructed out of pure symbols
alone. Indeed, the pure symbols are immutable, and it is not them that are
joined together by the syntax of the sentence, but occurrences of them --
replicas of them. My aim is to use the term "graph" for a graph-symbol,
although I dare say I sometimes lapse into using it for a graph-replica. To say
that a graph is scribed is accurate, because "to scribe" means to make a
graphical replica of. By "a line of identity," on the other hand, it is more
convenient to mean a replica of the linear graph of identity. For here the
indexical character is more positive; and besides, one seldom has occasion to
speak of the graph. But the only difference between a line of identity and an
ordinary dyadic spot is that the latter has its hooks marked at points that are
deemed appropriate without our being under any factual compulsion to mark them
at all, while a simple line such as is naturally employed for a line of
identity must, from the nature of things, have extremities which are at once
parts of it and of whatever it abuts upon. This difference does not prevent the
rules of the last list from holding good of such lines. The only occasion for
any additional rule is to meet that situation, in which no other graph-replica
than a line of identity can ever be placed, that of having a hook upon a sep. |
| |
|
|
| 501. |
As to this, it is to be remarked that an enclosure -- that is, a
sep with its contents -- is a graph; and those points on its periphery, that
are marked by the abuttal upon them of lines of identity, are simply the hooks
of the graph. But the sep is outside its own close. Therefore an unmarked point
upon it is just like any other vacant place outside the sep. But if a line
inside the sep is prolonged to the sep, at the instant of arriving at the sep,
its extremity suddenly becomes identified -- as a matter of fact, and there as
a matter of signification -- with a point outside the sep; and thus the
prolongation suddenly assumes an entirely different character from an ordinary,
insignificant prolongation. This gives us the following: Conditional Principle No.
4. Only the connexions and continuity of
lines of identity are significant, not their shape or size. The connexion or
disconnexion of a line of identity outside a sep with a marked or an unmarked
point on the sep follows the same rules as its connexion or disconnexion with
any other marked or unmarked point outside the sep, but the junction or
disjunction of a line of identity inside the sep with a point upon the sep
always follows the same rules as its connexion or disconnexion with a marked
point inside the sep.
In consequence of this principle, although the categorical rules
hitherto given remain unchanged in their application to lines of identity, yet
they require some modifications in their application to ligatures. |
| |
|
|
| 502. |
In order to see that the principle is correct, first consider Fig.
154. Now the rule of erasure of an unenclosed graph certainly allows the
transformation of this into Fig. 155, which must therefore be interpreted to
mean "Something is not ugly," and must not be confounded with Fig. 156,
"Nothing is ugly." But Fig. 156 is transformable into Fig. 157; that is, the
line of identity with a loose end can be carried to any vacant place within the
sep. If, therefore, Fig. 155 were to be treated as if the end of the line were
loose, it could be illatively transformed into Fig. 156. But the line can no
more be separated from the point of the sep than it could from any marked point
within the sep -- any more, for example, than |
| |
 |
 |
 |
 |
|
Figure 154 |
Figure 155 |
Figure 156 |
Figure 157 |
|
| |
Fig. 158, "Nothing good is ugly" could be transformed into Fig. 159, "Either
nothing is ugly or nothing is good." So Fig. 160 can, by the rule of insertion
within odd seps, be transformed to Fig. 161, and must be interpreted, like
that, "Everything acts on everything," and not, as in Fig. 162, "Everything
acts on something or other." But if the vacant point on the sep could be
treated like an ordinary point, Fig. 162 could be illatively transformed into
Fig. 160, which the interpretation forbids. Although in this argument special
graphs |
| |
 |
 |
 |
 |
 |
|
Figure 158 |
Figure 159 |
Figure 160 |
Figure 161 |
Figure 162 |
|
| |
are used, it is evident that the argument would be just the same whatever
others were used, and the proof is just as conclusive as if we had talked of
"any graph whatever, x," etc., as well as being clearer. The principle of
contraposition renders |
| |
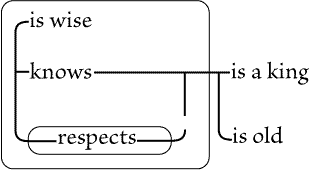 |
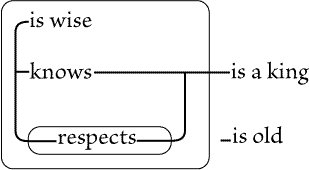 |
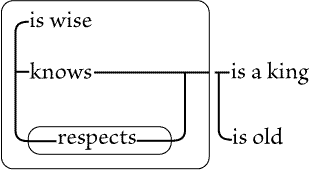 |
|
Figure 163 |
Figure 164 |
Figure 165 |
|
| |
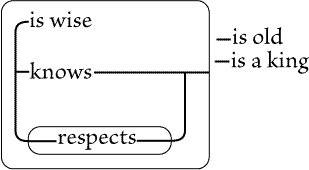 |
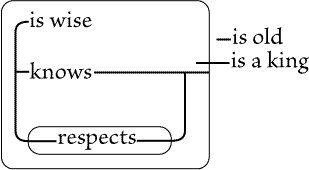 |
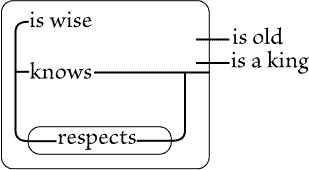 |
|
Figure 166 |
Figure 167 |
Figure 168 |
|
| |
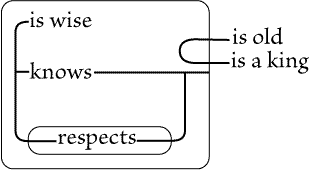 |
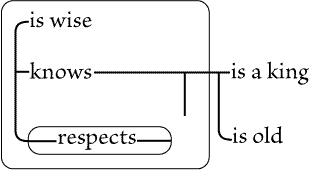 |
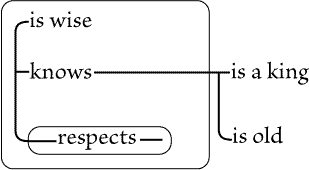 |
|
Figure 169 |
Figure 170 |
Figure 171 |
|
| |
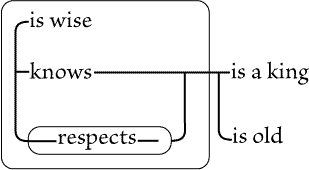 |
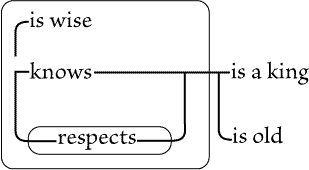 |
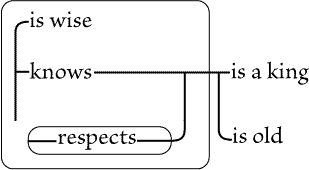 |
|
Figure 172 |
Figure 173 |
Figure 174 |
|
| |
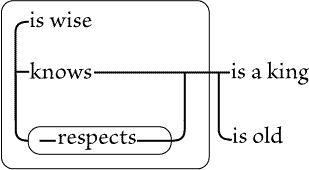 |
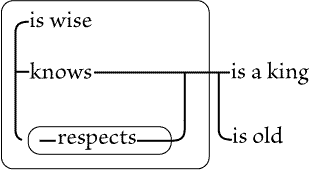 |
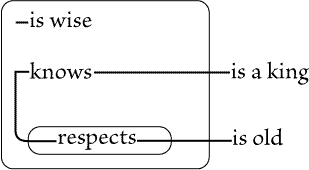 |
|
Figure 175 |
Figure 176 |
Figure 177 |
|
| |
|
| |
it evident that the same thing would hold for any finite nests of seps. |
|
| 503. |
On the other hand, it is easy to show that the illative connexion
or disconnexion of a line exterior to the sep with a point on the sep follows
precisely the same rules as if the point were outside of
and away from the sep Figs. 163-177 furnish grounds for the demonstration of this. Fig. 163
asserts that there is an old king whom every wise person that knows him
respects. The connexion of "is old" with "is king" can be illatively severed by
the rule of erasure, as in Fig. 164; so that the old person shall not be
asserted to be identical with the king whom all wise people that know him
respect; and once severed the connexion cannot be illatively restored. So it is
precisely if the line of identity outside the outer sep is cut at the sep, as
in Fig. 165, which asserts that somebody is respected by whatever wise person
there may be that knows him, and asserts that there is an old king, but fails
to assert that the old king is that respected person. Here, as before, the line
can be illatively severed but cannot be illatively restored. It is evident that
this is not because of the special significance of the "spots" or unanalyzed
rhemata, but that it would be the same in all cases in which a line of identity
should terminate at a point on a sep where a line inside that sep should also
terminate. Fig. 166 shows both lines broken, so that this might equally and for
the same reason result from the illative transformation of Fig. 164 or of Fig.
165. The lines, being broken as in Fig. 166, can be distorted in any way and
their extremities can be carried to any otherwise vacant places outside the
outer sep, and afterwards can be brought back to their present places. In this
respect, a vacant point on a sep is just like any other vacant point outside
the close of the sep. If the line of identity attached to "is old" be carried
to the sep, as in Fig. 167, certainly no addition is thereby made to the
assertion. Once the ligature is carried as far as the sep, the rule of
insertion within an odd number of seps permits it to be carried still further,
as is done in Fig. 167, with the ligature attached to "is a king." This whole
graph may be interpreted, "Something is old and something is a king." But this
last does not exist unless something is respected by whatever that is wise
there may be that knows it. The graph of Fig. 167 can be illatively
retransformed into Fig. 166, by first severing the ligature attached to "is a
king" outside the sep by the rule of erasure, when the part of the ligature
inside may be erased by the rule of deiteration, and finally the part outside
the close of the sep may be erased by the rule of erasure. On the other hand
the ligatures attached in Fig. 167 to "is old" and "is a king" might, after
Fig. 167 had been converted in Fig. 168, be illatively joined inside the sep by
the rule of insertion, as in Fig. 169, which asserts that there is something
old and there is a king; and if there is an old king something is respected by
whatever wise thing there may be that knows it. This is not illatively
retransformable in Fig. 168. It thus abundantly shows that an unenclosed line
can be extended to a point on an unenclosed sep under the same conditions as to
any other unenclosed point. For there is evidently nothing peculiar about the
characters of being old and of being a king which render them different in this
respect from graphs in general. Let us now see how it is in regard to singly
enclosed lines in their relations to points on seps in the same close. If in
Fig. 163 we sever the ligature denoting the object accusative of "respects,"
just outside the inner sep, as in Fig. 170, the interpretation becomes, "There
is an old king, and whoever that is wise there may be who knows him, respects
everybody." This is illatively transformable into Fig. 163 by the rule of
insertion under odd enclosures, just as if the marked point on the sep were a
hook of any spot. We may, of course, by the rule of erasure within even seps,
cut away the ligature from the sep internally, getting Fig. 171, "There is an
old king, whom anybody that knows respects somebody or other." The point on the
sep being now unmarked, it makes no difference whether the outside ligature is
extended to it, as in Fig. 172, or not. It is the same if the ligature denoting
the subject nominative of "respects" be broken outside the inner sep, as in
Fig. 174. Whether this be done, or whether the line of identity joining "is
wise" to "knows" be cut, as in Fig. 173, in either case we get a graph
illatively transformable into Fig. 163, but not derivable from Fig. 163 by any
illative transformation. If, however, the line of identity within the inner sep
be retracted from the sep, as in Figs. 175 and 176, it makes no difference
whether the line outside the sep be extended to the unmarked point on the sep
or not. One cannot even say that one form of interpretation better fits the one
figure and another the other: they are absolutely equivalent. Thus, the
unmarked point on the oddly enclosed sep is just like any other unmarked point
exterior to the close of the sep as far as its relations with exterior lines of
identity are concerned. |
| |
|
|
| 504. |
The principle of contraposition extends this Conditional Principle
No. 4 to all seps, within any finite number of seps. By means of this principle the rules of illative transformation
hitherto given will easily be extended so as to apply to graphs with ligatures
attached to them, and the one rule which it is necessary to add to the list
will also be readily deduced. In the following statement, each rule will first
be enunciated in an exact and compendious form and then, if necessary, two
remarks will be added, under the headings of "Note A" and "Note B." Note A will
state more explicitly how the rule applies to a line of identity; while Note B
will call attention to a transformation which might, without particular care,
be supposed to be permitted by the rule but which is really not permitted. |
| |
|
|
| |
C. Basic Categorical Rules for the Illative Transformation
of All GraphsP |
| 505. |
Rule 1. Called
The rule of Erasure and of Insertion. In even seps,
any graph-replica can be erased; in odd seps any graph-replica can be inserted.
Note A. By even seps is meant any finite even number of seps, including
none; by odd seps is meant any odd number of seps.
This rule permits any ligature, where evenly enclosed, to be severed,
and any two ligatures, oddly enclosed in the same seps, to be joined. It
permits a branch with a loose end to be added to or retracted from any line of
identity.
It permits any ligature, where evenly enclosed, to be severed from the
inside of the sep immediately enclosing that evenly enclosed portion of it, and
to be extended to a vacant point of any sep in the same enclosure. It permits
any ligature to be joined to the inside of the sep immediately enclosing that
oddly enclosed portion of it, and to be retracted from the outside of any sep
in the same enclosure on which the ligature has an extremity.
Note B. In the erasure of a graph by this
rule, all its ligatures must be cut. The rule does not
permit a sep to be so inserted as to intersect any
ligature, nor does it permit any erasure to accompany an
insertion
It does not permit the insertion of a sep within even seps |
| |
|
|
| 506. |
Rule 2. Called
The Rule of Iteration and Deiteration. Anywhere
within all the seps that enclose a replica of a graph, that graph may be
iterated with identical ligations, or being iterated, may be deiterated. Note A. The operation of iteration consists in the insertion of a new
replica of a graph of which there is already a replica, the new replica having
each hook ligated to every hook of a graph-replica to which the corresponding
hook of the old replica is ligated, and the right to iterate includes the right
to draw a new branch to each ligature of the original replica inwards to the
new replica. The operation of deiteration consists in erasing a replica which
might have illatively resulted from an operation of iteration, and of
retracting outwards the ligatures left loose by such erasure until they are
within the same seps as the corresponding ligature of the replica of which the
erased replica might have been the iteration.
The rule permits any loose end of a ligature to be extended inwards
through a sep or seps or to be retracted outwards through a sep or seps. It
permits any cyclical part of a ligature to be cut at its innermost part, or a
cycle to be formed by joining, by inward extensions, the two loose ends that
are the innermost parts of a ligature. If any hook of the original replica of the iterated graph is ligated to
no other hook of any graph-replica, the same should be the case with the new
replica. Note B. This rule does not confer a right to ligate any hook to another
nor to deligate any hook from another unless the same hooks, or corresponding
hooks of other replicas of the same graphs (these replicas being outside every
sep that the hooks ligated or deligated are outside), be ligated otherwise, and
outside of every sep that the new ligations or deligations are outside of.
This rule does not confer the right to extend any
ligature outwardly from within any sep, nor to retract
any ligature inwardly from without any sep. |
| |
|
|
|
507. |
Rule
3. Called The Rule of Assertion. Any graph
well-understood to be true may be scribed unenclosed.
Note A. This rule is to be understood as permitting the explicit
assertion of three classes of propositions; first, those that are involved in
the conventions of this system of existential graphs; secondly, any
propositions known to be true but which may not have been thought of as
pertinent when the graph was first scribed or as pertinent in the way in which
it is now seen to be pertinent (that is to say, premisses may be added if they
are acknowledged to be true); thirdly, any propositions which the scription of
the graph renders true or shows to be true. Thus, having graphically asserted
that it snows, we may insert a graph asserting "that it snows is asserted" or
"it is possible to assert that it snows without asserting that it is winter." |
| |
|
|
| 508. |
Rule 4. Called
The Rule of Biclosure. Two seps, one within the
other, with nothing between them whose significance is affected by seps, may be
withdrawn from about the graph they doubly enclose. Note A. The significance of a ligature is not affected by a sep except
at its outermost part, or if it passes through the close of the sep; and
therefore ligatures passing from outside the outer sep to inside the inner one
will not prevent the withdrawal of the double sep; and such ligatures will
remain unaffected by the withdrawal.
Note B. A ligature passing twice through the outer sep without passing
through the inner one, or passing from within the inner one into the
intermediate space and stopping there, will be equivalent to a graph and will
preclude the withdrawal. |
| |
|
|
| 509. |
Rule 5. Called
The Rule of Deformation. All parts of the graph may
be deformed in any way, the connexions of parts remaining unaltered; and the
extension of a line of identity outside a sep to an otherwise vacant point on
that sep is not to be considered to be a connexion. |
| |
|
|
| |
Chapter 5: The Gamma Part of Existential Graphs |
| |
CHAPTER 5 |
| |
THE GAMMA PART OF EXISTENTIAL GRAPHS(*1) |
| 510. |
The alpha part of graphs . . . is able to represent no reasonings
except those which turn upon the logical relations of general terms. |
| |
|
|
| 511. |
The beta part . . . is able to handle with facility and dispatch reasonings of a very intricate kind, and propositions which ordinary language
can only express by means of long and confusing circumlocutions. A person who
has learned to think in beta graphs has ideas of the utmost clearness and
precision which it is practically impossible to communicate to the mind of a
person who has not that advantage. Its reasonings generally turn upon the
properties of the relations of individual objects to one another. But it is able to do nothing at all with many ideas which we are all
perfectly familiar with. Generally speaking it is unable to reason about
abstractions. It cannot reason for example about qualities nor about relations
as subjects to be reasoned about. It cannot reason about ideas. It is to supply
that defect that the gamma part of the subject has been invented. But this
gamma part is still in its infancy. It will be many years before my successors
will be able to bring it to the perfection to which the alpha and beta parts
have been brought. For logical investigation is very slow, involving as it does
the taking up of a confused mass of ordinary ideas, embracing we know not what
and going through with a great quantity of analyses and generalizations and
experiments before one can so much as get a new branch fairly inaugurated. . .
. |
| |
|
|
| 512. |
The gamma part of graphs, in its present condition, is
characterized by a great wealth of new signs; but it has no sign of an
essentially different kind from those of the alpha and beta part. The alpha
part has three distinct kinds of signs, the graphs, the sheet of assertion, and
the cuts. The beta part adds two quite different kinds of signs, spots, or lexeis, and ligatures with selectives. It is true that a line of identity is a
graph; but the terminal of such a line, especially a terminal on a cut where
two lines of identity have a common point, is radically different. So far, all
the gamma signs that have presented themselves, are of those same kinds. If
anybody in my lifetime shall discover any radically disparate kind of sign,
peculiar to the gamma part of the system, I shall hail him as a new Columbus.
He must be a mind of vast power. But in the gamma part of the subject all the
old kinds of signs take new forms. . . . Thus in place of a sheet of assertion,
we have a book of separate sheets, tacked together at points, if not otherwise
connected. For our alpha sheet, as a whole, represents simply a universe of
existent individuals, and the different parts of the sheet represent facts or
true assertions made concerning that universe. At the cuts we pass into other
areas, areas of conceived propositions which are not realized. In these areas
there may be cuts where we pass into worlds which, in the imaginary worlds of
the outer cuts, are themselves represented to be imaginary and false, but which
may, for all that, be true, and therefore continuous with the sheet of
assertion itself, although this is uncertain. You may regard the ordinary blank
sheet of assertion as a film upon which there is, as it were, an undeveloped
photograph of the facts in the universe. I do not mean a literal picture,
because its elements are propositions, and the meaning of a proposition is
abstract and altogether of a different nature from a picture. But I ask you to
imagine all the true propositions to have been formulated; and since facts
blend into one another, it can only be in a continuum that we can conceive this
to be done. This continuum must clearly have more dimensions than a surface or
even than a solid; and we will suppose it to be plastic, so that it can be
deformed in all sorts of ways without the continuity and connection of parts
being ever ruptured. Of this continuum the blank sheet of assertion may be
imagined to be a photograph. When we find out that a proposition is true, we
can place it wherever we please on the sheet, because we can imagine the
original continuum, which is plastic, to be so deformed as to bring any number
of propositions to any places on the sheet we may choose. |
| |
|
|
| 513. |
So far I have called the sheet a photograph, so as not to
overwhelm you with all the difficulties of the conception at once. But let us
rather call it a map -- a map of such a photograph if you like. A map of the
simplest kind represents all the points of one surface by corresponding points
of another surface in such a manner as to preserve the continuity unbroken,
however great may be the distortion. A Mercator's chart, however, represents
all the surface of the earth by a strip, infinitely long, both north and south
poles being at infinite distances, so that places near the poles are magnified
so as to be many times larger than the real surfaces of the earth that they
represent, while in longitude the whole equator measures only two or three
feet; and you might continue the chart so as to represent the earth over and
over again in as many such strips as you pleased. Other kinds of map, such as
my Quincuncial Projection which is drawn in the fourth volume of the American
Journal of Mathematics,(*1) show the whole earth over and over again in checkers,
and there is no arrangement you can think of in which the different
representations of the same place might not appear on a perfectly correct map.
This accounts for our being able to scribe the same graph as many times as we
please on any vacant places we like. Now each of the areas of any cut
corresponds exactly to some locus of the sheet of assertion where there is
mapped, though undeveloped, the real state of things which the graph of that
area denies. In fact it is represented by that line of the sheet of assertion
which the cut itself marks. |
| |
|
|
| 514. |
By taking time enough I could develop this idea much further, and
render it clearer; but it would not be worth while, for I only mention it to
prepare you for the idea of quite different kinds of sheets in the gamma part
of the system. These sheets represent altogether different universes with which
our discourse has to do. In the Johns Hopkins Studies in Logic(*1) -- I printed a
note of several pages on the universe of qualities -- marks, as I then called
them. But I failed to see that I was then wandering quite beyond the bounds of
the logic of relations proper. For the relations of which the so-called "logic
of relatives" treats are existential relations, which the nonexistence of
either relate or correlate reduces to nullity. Now, qualities are not, properly
speaking, individuals. All the qualities you actually have ever thought of
might, no doubt, be counted, since you have only been alive for a certain
number of hundredths of seconds, and it requires more than a hundredth of a
second actually to have any thought. But all the qualities, any one of which
you readily can think of, are certainly innumerable; and all that might be
thought of exceed, I am convinced, all multitude whatsoever. For they are mere
logical possibilities, and possibilities are general, and no multitude can
exhaust the narrowest kind of a general. Nevertheless, within limitations,
which include most ordinary purposes, qualities may be treated as individuals.
At any rate, however, they form an entirely different universe of existence. It
is a universe of logical possibility. As we have seen, although the universe of
existential fact can only be conceived as mapped upon a surface by each point
of the surface representing a vast expanse of fact, yet we can conceive the
facts [as] sufficiently separated upon the map for all our purposes; and in the
same sense the entire universe of logical possibilities might be conceived to
be mapped upon a surface. Nevertheless, in order to represent to our minds the
relation between the universe of possibilities and the universe of actual
existent facts, if we are going to think of the latter as a surface, we must
think of the former as three-dimensional space in which any surface would
represent all the facts that might exist in one existential universe. In
endeavoring to begin the construction of the gamma part of the system of
existential graphs, what I had to do was to select, from the enormous mass of
ideas thus suggested, a small number convenient to work with. It did not seem
to be convenient to use more than one actual sheet at one time; but it seemed
that various different kinds of cuts would be wanted. |
| |
|
|
| 515. |
I will begin with one of the gamma cuts. I call it the broken cut.
I scribe it thus |
| |
 |
|
Figure 178 |
|
| |
This does not assert that it does not rain. It only asserts that the alpha and
beta rules do not compel me to admit that it rains, or what comes to the same
thing, a person altogether ignorant, except that he was well versed in logic so
far as it embodied in the alpha and beta parts of existential graphs, would not
know that it rained.(*1) |
| |
|
|
| 516. |
The rules of
this cut are very similar to those of the alpha cut.
Rule 1. In a broken cut already
on the sheet of assertion any graph may be inserted.
Rule 2. An evenly enclosed
alpha cut may be half erased so as to convert it into a
broken cut, and an oddly enclosed broken cut may be
filled up to make an alpha cut. Whether the enclosures
are by alpha or broken cuts is indifferent.
Consequently |
| |
 |
|
Figure 179 |
|
| |
will mean that the graph
g is beta-necessarily true.(*1) By Rule 2, this is
converted into |
| |
 |
|
Figure 180 |
|
| |
which is equivalent to |
| |
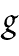 |
|
Figure 181 |
|
| |
the simple assertion of
g. By the same rule Fig. 180 is transformable into |
| |
 |
|
Figure 182 |
|
| |
which means that the beta rules do not make
g false.(*2)
That is g is beta-possible.(*3)
So if we start from |
| |
 |
|
Figure 183 |
|
| |
which denies the last figure and thus asserts that it is beta-impossible that
g
should be true,(*4) Rule 2 gives |
| |
 |
equivalent to |
 |
|
Figure 184 |
|
Figure 185 |
|
| |
the simple denial of
g.(*5) And from this we get again |
| |
|
| |
|
|
| 517. |
It must be remembered that possibility and necessity are relative
to the state of information. Of a certain graph g let us suppose that I am in such a state of
information that it may be true and may be false; that is I can
scribe on the sheet of assertion Figs. 182 and 186. Now
I learn that it is true. This gives me a right to scribe
on the sheet Figs. 182, 186 and 181. But now relative to
this new state of information, Fig. 186 ceases to be
true; and therefore relatively to the new state of
information we can scribe Fig. 179.(*1) |
| |
|
|
| 518. |
You thus perceive that we should fall into inextricable confusion
in dealing with the broken cut if we did not attach to it a sign to distinguish
the particular state of information to which it refers. And a similar sign has
then to be attached to the simple g, which refers to the state of information
at the time of learning that graph to be true. I use for this purpose cross
marks below, thus: |
| |
 |
|
Figure 187 |
|
| |
These selectives are very peculiar in that they refer to states of information
as if they were individual objects. They have, besides, the additional
peculiarity of having a definite order of succession, and we have the rule that
from Fig. 188 we can infer Fig. 189.(*1) |
| |
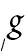 |
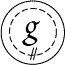 |
|
Figure 188 |
Figure 189 |
|
| |
These signs are of great use in cleaning up the confused doctrine of modal
propositions as well as the subject of logical breadth and depth. |
| |
|
|
| 519. |
There is not much utility in a double broken cut. Yet it may be
worth notice that Fig. 181 and |
| |
 |
|
Figure 190 |
|
| |
can neither of them be inferred from the other. The outer
of the two broken cuts is not only relative to a state of information but to a
state of reflection. The graph [190] asserts
that it is possible that the truth of the graph g is necessary. It is only
because I have not sufficiently reflected upon the subject that I can have any
doubt of whether it is so or not. |
| |
|
|
| 520. |
It becomes
evident, in this way, that a modal proposition is a
simple assertion, not about the universe of things, but
about the universe of facts that one is in a state of
information sufficient to know. [Fig. 186] without any
selective, merely asserts that there is a possible state
of information in which the knower is not in a condition
to know that the graph g is true, while Fig. 179 asserts
that there is no such possible state of information.
Suppose, however, we wish to assert that there is a
conceivable state of information of which it would not
be true that, in that state, the knower would not be in
condition to know that g is true. We shall naturally
express this by Fig. 191. |
| |
 |
|
Figure 191 |
|
| |
But this is to
say that there is a conceivable state of information in
which the knower would know Fig. 191 that g is true.
[This is expressed by] Fig. 188. |
| |
|
|
|
521. |
Now suppose we wish to assert that
there is a conceivable state of information in which the
knower would know g to be true and yet
would not know another graph h to be true.
We shall naturally express this by Fig. 192. |
| |
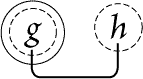 |
|
Figure 192 |
|
| |
Here we have a new kind of ligature, which will follow all the rules of
ligatures. We have here a most important addition to the system of graphs.
There will be some peculiar and interesting little rules, owing to the fact
that what one knows, one has the means of knowing that one knows -- which is
sometimes incorrectly stated in the form that whatever one knows, one knows
that one knows, which is manifestly false. For if it were the same to say "A
whale is not a fish" and "I know that a whale is not a fish," the precise
denials of the two would be the same. Yet one is "A whale is a fish" and the
other is "I do not know that a whale is not a fish." |
| |
|
|
| 522. |
The truth is that it is necessary to have a graph to signify that
one state of information follows after another. If we scribe,
 to express that the state of information B follows after the state of
information A, we shall have to express that the state of information B follows after the state of
information A, we shall have |
| |
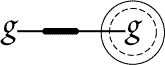 |
|
Figure 193 |
|
| |
|
|
| 523. |
It is clear, however, that the matter must not be allowed to rest
here. For it would be a strangely, and almost an ironically, imperfect kind of
logic which should recognize only ignorance and should ignore error. Yet in
order to recognize error in our system of graphs, we shall be obliged still
further to introduce the idea of time, which will bring still greater
difficulties. Time has usually been considered by logicians to be what is
called "extra-logical" matter. I have never shared this opinion.(*1) But I have
thought that logic had not reached that state of development at which the
introduction of temporal modifications of its forms would not result in great
confusion; and I am much of that way of thinking yet. The idea of time really
is involved in the very idea of an argument. But the gravest complications of
logic would be involved, [if we took] account of time [so as] to distinguish
between what one knows and what one has sufficient reason to be entirely
confident of. The only difference, that there seems to be room for between
these two, is that what one knows, one always will have reason to be confident
of, while what one now has ample reason to be entirely confident of, one may
conceivably in the future, in consequence of a new light, find reason to doubt
and ultimately to deny. Whether it is really possible for this to occur,
whether we can be said truly to have sufficient reason for entire confidence
unless it is manifestly impossible that we should have any such new light in
the future, is not the question. Be that as it may, it still remains
conceivable that there should be that difference, and therefore there is a
difference in the meanings of the two phrases. I confess that my studies
heretofore have [not] progressed so far that I am able to say precisely what
modification of our logical forms will be required when we come to take
account, as some day we must, of all the effects of the possibilities of error,
as we can now take account, in the doctrine of modals, of the possibilities of
ignorance. Nor do I believe that the time has yet come when it would be
profitable to introduce such complications. But I can see that, when that time
does come, our logical forms will become very much more metamorphosed, by
introducing that consideration, than they are in modal logic, where we take
account of the possibility of ignorance as compared with the simple logic of
propositions de inesse (as non-modal propositions, in which the ideas of
possibility and necessity are not introduced, are called) . . . |
| |
|
|
|
524. |
I introduce certain spots which I term Potentials. They are shown
on this diagram: |
| |
 |
| |
|
|
| 525. |
It is obvious that the lines of identity on the left-hand side of
the potentials are quite peculiar, since the characters they denote are not,
properly speaking, individuals. For that reason and others, to the left of the
potentials I use selectives not ligatures. |
| |
|
|
| 526. |
As an example of the use of the potentials, we may take this
graph, which expresses a theorem of great importance: The proposition is that
for every quality Q whatsoever, there is a dyadic relation, R, such that,
taking any two different individuals both possessing this quality, Q, either
the first stands in the relation R to some thing to which the second does not
stand in that relation, while there is nothing to which the second stands in
that relation without the first standing in the same relation to it; or else it
is just the other way, namely that the second stands in the relation, R, to
which the first does not stand in that relation, while there is nothing to
which the first stands in that relation, R, without the second also standing in
the same relation to it. The proof of this, which is a little too intricate to
be followed in an oral statement |
| |
|
| |
(although in another lecture
(*1) I shall substantially prove it) depends upon
the fact that a relation is in itself a mere logical possibility. |
| |
|
|
|
527. |
I will now
pass to another quite indispensable department of the
gamma graphs. Namely, it is necessary that we should be
able to reason in graphs about graphs. The reason is
that a reasoning about graphs will necessarily consist
in showing that something is true of every possible
graph of a certain general description. But we cannot
scribe every possible graph of any general description,
and therefore if we are to reason in graphs we must have
a graph which is a general description of the kind of
graph to which the reasoning is to relate. |
| |
|
|
| 528. |
For the alpha
graphs, it is easy to see what is wanted. Let
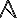 , the old Greek form of the letter A, denote the sheet of
assertion. Let , the old Greek form of the letter A, denote the sheet of
assertion. Let 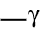 be "is a graph." Let be "is a graph." Let
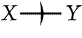 mean that
X is
scribed or placed on Y. Let mean that
X is
scribed or placed on Y. Let
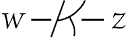 mean that
Z is the area of the cut W. Let mean that
Z is the area of the cut W. Let
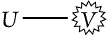 mean that
U is a graph, precisely expressing V. It is
necessary to place V in the saw-rim, as I call the line about it, because in
thus speaking of a sign materialiter, as they said in the middle ages, we
require that it should have a hook that it has not got. For example mean that
U is a graph, precisely expressing V. It is
necessary to place V in the saw-rim, as I call the line about it, because in
thus speaking of a sign materialiter, as they said in the middle ages, we
require that it should have a hook that it has not got. For example |
| |
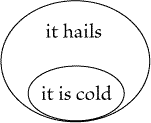 |
|
Figure 195 |
|
| |
asserts, of course, that if it hails, it is cold de inesse. Now a graph asserting that this graph is scribed on the sheet of assertion,
will be |
| |
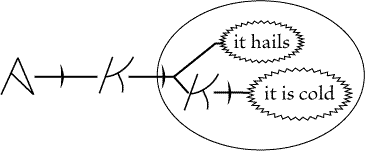 |
|
Figure 196 |
|
| |
This graph only asserts what the other does assert. It does not say what the
other does not assert. But there would be no difficulty in expressing that. We
have only to place instead of
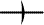 ,
wherever it occurs, ,
wherever it occurs,
 |
| |
|
|
| 529. |
We come now to the graphical expressions of beta graphs. Here we
require the following symbols,(*1) |
| |
 |
|
| |