| Existential Graphs - 4.418-529 - Notes | ||
| 418 | *1 | From "Logical Tracts, No. 2," c. 1903. "Logical Tracts, No. 1" is largely a repetition of the papers on signs in vol. 2, bk. II, ch. 2. |
| *2 | Most of the terms such as "representamen," "icons," "indices," etc. are defined in vol. 2, bk. II, ch. 2. | |
| 423 | *1 | This does not seem to have been written |
| 424 | *1 | These conventions, together with No. 3, define the Alpha Part of Graphs. |
| *2 | E.g., Schröder; see 3.510ff. | |
| 426 | *1 | Vorlesungen über die Algebra der Logik, Bd. 3, §23 and §31, (1895). |
| 434 | *1 | See 3.468ff. |
| 435 | *P1 | In the language of logic "consequence" does not mean that which follows, which is called the consequent, but means the fact that a consequent follows from an antecedent. |
| *1 | See 515f. on the broken cut. | |
| 438 | *1 | The conventions Nos. 4 to 12 define the Beta Part of Graphs. |
| *P1 | This, it will be remarked, makes what modern
grammars call the
direct and indirect objects, as well as much else, to be subjects;
and some
persons will consider this to be a bad abuse of the word subject.
Come, let us
have this out. I grant you that in polite literature usage is, not
only almost,
but altogether, the arbitrium et jus et norma loquendi. And if I am
asked whose
usage, I reply, that of the public whom you are addressing. If, with
Vaugelas
[Remarques sur la langue française], you are addressing the court,
then the
usage of the court. If you are lecturing the riffraff of a great
city, then
their usage. If anybody were to dispute this and ask me to prove it,
I should
reply that whatever ultimate purpose the polite littérateur may
have, it is
indispensable to that purpose that he should make the reading of
what he writes
agreeable; and in order that it may be agreeable, it is necessary
that it
should be easily understood by those who are addressed. But with
logical
writings it is different. If there be any sciences which can
flourish without
any words having any exact meanings, logic is not one of them. It
cannot pursue
its truths without a terminology of which every word shall have a
single exact
definition. To a great extent it already possesses such a
terminology,
notwithstanding the frequent abuse of its terms. But where this
terminology is
unsettled, to follow usage would simply be to prolong the confusion.
There are
conflicting individual predilections which must be made to give way;
and there
is only one thing to which they will consent to give way. It is some
rational
principle; which, stated generally, will recommend itself to all.
Where are we
to seek such a principle? In experience. He must profit by the
experience of
those sciences which have had the greatest difficulties with their
terminology,
and which have successfully surmounted those difficulties. Wherever
this has
been accomplished, it has been by adopting a rational general
principle; and
that principle has always been essentially the same. Any taxonomic
zoölogist or
botanist will tell you what it is. He who introduces a conception
into the
science shall have the right and the duty of assigning to it a
suitable
technical expression; and whoever thereafter uses that expression,
technically
in any other sense commits a grave misdemeanor, since he thereby
inflicts an
injury upon the science. [Cf. 2.219-26.] Now let us apply this rule to the word subject. This was made a term of logic about A.D. 500 with this definition: "Subjectum est dequo dicitur id quod praedicatur" (Boethii Opera, Eds. of 1546 and 1570, p. 823, in Comm. in Ciceronis Topica, lib. v.) Now unless we were prepared to say that for different languages there are different doctrines of logic (which would be contrary to the essence of logic, as all will admit) we cannot, in this definition, take the preposition de in so narrow a sense as to exclude the grammatical accusative, dative, genitive and ablative of the verb. For dispersed through all the families of speech there are a dozen languages which either habitually or frequently express a proposition completely without putting any noun in the nominative. Among the European languages, Gaelic is an example, in which the principal subject is most commonly put in the genitive. But the logical fact is simply that it frequently makes a difference in the sense of a proposition which of the different nouns, naming objects to which the verb refers, is considered to be immediately attached to the verb, which to the combination of these two, and so on. Thus, in the sentence, "Some angel gives every man some gift," the verb "gives" is directly applied to "some gift," making "gives-a-gift"; then this action of gift-giving is applied to "every man"; finally the compound "gives-gift to every man" is applied to a certain angel; while in the sentence "A certain gift (perhaps, speech) is given to every man by some angel or other" the verb "is given by" is applied directly to "some angel," making "is angel-given to," which is applied to "every man," and then "is angel-given to every man" is applied to a certain gift. One sentence represents one angel as distributing gifts to all men, the other represents one gift as bestowed by one or another angel on each man. Thus, the subject-nominative is ordinarily of all the subjects the one of which the verb is least directly said. I quite admit that I use the word subject as Boëthius never contemplated its being used; but it would be destructive to science to say that a term must be applied to nothing that its originator did not contemplate its being applied to. It is the definition only that holds. As a term of grammar, the word subject did not come into use until late in the eighteenth century. It would be somewhat impertinent, therefore, for grammarians to claim that, to their usage, the millennial usage of those from whom they borrowed the term, must bow. |
|
| 447 | *1 | Cf. vol. 2, bk. II, ch. 2, §5. |
| 449 | *P1 | This will be proved in a later note. [This was not done, but see 472f., 561n.] |
| 455 | *1 | Cf. 564n. |
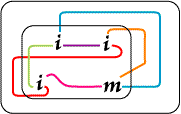
| 460 | z1 | Here is a version of Figure 109
scibed as it might be by modern existential graphs software; the
colors are completely consistent with Peirce's own practice in his
manuscripts; we are freed from many of the limits on typography
under which he labored.
The colors eliminate many of the difficulties associated with sorting out lines of identity in a diagram (Jay Zeman). |
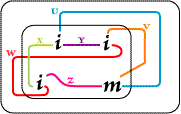
| z2 | Note that one of the Selectives
(shown as v in the original printed illustration) has been
changed to u, which is the appropriate notation given the
Lines of Identity in Figure 109. As a transition to the diagrams
employing Selectives, we offer the following diagram (Jay
Zeman).:
|
|
| 462 | *1 | To illustrate this, two complicated graphs are given. They are not reproduced because the ambiguity in Peirce's explanations makes them unilluminating. |
| 463 | *1 | This section deals in part with the Gamma Part of Graphs; see particularly 470-471. Cf. also 516ff. |
| 469 | *1 | I.e., the Gamma Part of Graphs. |
| 471 | *1 | Bk. I, Postulate 5. |
| 474 | *1 | But see 579. |
| 476 | *1 | Cf. 2.186ff. |
| 480 | *P1 | Some reader may think that I am expending energy in trying to explain what needs no explanation. He may argue that the mathematician reasons about a diagram in which there appears to be nothing at all corresponding to the structure of the proposition -- no predicate and subjects. Nor does the mathematician's premiss or conclusion at all pretend to represent the diagram in that respect. It may seem to this reader satisfactory to say that the conclusion follows from the premiss, because the premiss is only applicable to states of things to which the conclusion is applicable. If he thinks that satisfactory, the purpose of this tract does not compel me to dispute it. It is only to defend myself against the charge of giving a needless and doubtful explanation that I point out that it is precisely this relation of applicability that requires to be explained. How comes it that the conclusion is applicable whenever the premiss is applicable? I suppose the answer will be that its only meaning is a part of what the premiss means. The "meaning" of a proposition is what it is intended to convey. But when a mathematician lays down the premisses of the theory of numbers, it cannot be said that he then intends to convey all the propositions of that theory, of which the great majority will occasion him much surprise when he comes to learn them. If to avoid this objection a distinction be drawn between what is explicitly intended and what is implicitly intended, I submit that this manifestly makes a vicious circle; for what can it be implicitly to intend anything, except to intend whatever may be a necessary consequence of what is explicitly intended? |
| 483 | *1 | In 439-40 |
| 494 | *1 | Cf. 2.356. |
| 500 | *1 | In 447. |
| 510 | *1 | From "Lowell Lectures of 1903." Lecture IV |
| 513 | *1 | Vol. 2, pp. 394-6 (1879); to be published in vol. 7 |
| 514 | *1 | *2 See 2.517ff. |
| 515 | *1 | I.e., It is possible that it does not rain. |
| 516 | *1 | *2 I.e., It is false that g is possibly false. |
| *2 | *1 I.e., It is possibly false that g is false; or it is possible that g is true. | |
| *3 |
*2 The passage from Figs. 179 to 181, from 181 to
182, and from 179 to 182 represent C. I.
Lewis' subsequent "strict implications," 4.1, 4.12, 4.13
respectively. See his Survey of Symbolic Logic, p. 306-7. The
broken cut represents Lewis's
|
|
| *4 | *3 I.e., g is impossible. | |
| *5 | *4 This transition is Lewis' 1.7, ibid., p. 295. | |
| *6 | *5 I.e., g is not necessary, or it is possible that g is false. 183-6 is the transformation 179-182 with ~g substituted for g | |
| 517 | *1 | *6 I.e., if g be possibly true and false, and also true, it is necessarily true. |
| 518 | *1 | I.e., with respect to the given state of information, if g is true, it is necessarily true. |
| 523 | *1 | Cf. 3.446 |
| 526 | z1 | The colored Ligatures are, again, a latter-day alteration for clarity which is completely consistent with Peirce's own practice in his manuscipts (Jay Zeman). |
| *1 | That lecture is not being published. | |
| 529 | *1 | The following was found on a separate sheet, apparently for use in a similar lecture: |
|
|
||