J. Jay Zeman
Interest in orthomodular (OM) logic coupled with the fact that the definition of classical implication on any lattice renders that lattice distributive has led to a number of studies -- mainly proof theoretical -- of the effects of defining non-classical implications on orthomodular lattices (OML's) (see [9, 5, 4] , for example). Although a number of such implications have been shown to preserve the non-distributive character of the OML, a systematic study of the semantics for such functions has been lacking; this, of course, makes it difficult to discuss empirical interpretations of OM logic with implication.
I would argue that a 'logic' without an implication function susceptible of reasonable interpretation is radically incomplete, and indeed, hardly qualifies as a theory of deduction. The purpose of this article, then, will be to provide an appropriate semantics for OM logic, for OM logic, that is, as supplemented by implications drawn from an important family of conditional functions. These functions we will call the 'normal implications'; a normal implication, proof-theoretically, is an implicational calculus whose set of theorems includes the pure strict implicational fragment of K, the most general normal modal logic of Segerberg [6] (K was also studied in [8] under the name T°). After setting down a basic axiomatization for OM logic including K's strict implicational part, we shall provide a formal semantics based on the 'Operational statistics' of Foulis and Randall [1, 2] ; this semantics is an extension of both classical probability theory and classical modal semantics and incidentally promises, I think, an important conceptual nexus between the two. A completeness result for the basic system will be set down; extensions will be briefly discussed, and finally some possible empirical interpretations will be mentioned.
1. THE SYSTEM OK
OK, our basic system, will have as primitives as many atomic formulas as you care to count, plus the unary connective N and the binary K and C.
For a number of reasons it will be convenient to consider OK a sequent logic;
'![]() ' is then also an
object symbol, forming sequents in the pattern
' is then also an
object symbol, forming sequents in the pattern
A proof in OK is a set of sequents each of which is G
![]() a such that either:
a such that either:
|
|
a Î G, or | |||||||||
|
|
h, q Î G and a = Khq , or | |||||||||
|
|
a
is an axiom, or is derived (G
|
|||||||||
|
|
|
|||||||||
|
|
|
|||||||||
|
|
|
|||||||||
|
|
|
AXIOM SCHEMATA:
| N1: | CÆa |
| N2: | CCaNbCbNa |
| N3: | CNNaa |
| OM: | CCabCbAKbNaa |
| CC: | CKCabANCabgg |
DEFINITIONS:
| 1 | for | any a such that
|
| Æ | for | KaNa |
| Eab | for | KCabCba |
| La | for | C1a |
| Ma | for | NLNa |
| Pab | for | CKaANabb |
Pab is read "a
is compatible with b"; in the algebraic
representation of OK we shall present, this is the standard sense of
compatibility, i.e., a and b
belong to the same block of an OML; note that the definition associates the
compatibility of a and b
with classical modus ponens' 'working' for a and b
. Extended discussions of compatibility and OML's are available (see [3,
5] );
on an intuitive level, compatible assertions are those whose deductive
relationships are those of the classical logic. Note that axiom schema CC could
be set down simply as PCabg, which is to say
that all implications are universally compatible, i.e., are center-valued in the
lattices of propositions. Incidentally, postulate
![]() K is characteristic of the pure strict implicational fragment of K [7]
.
K is characteristic of the pure strict implicational fragment of K [7]
.
2. DEDUCTIVE LATTICE STRUCTURES
Consider the set X of all wffs of a C-K-N primitive system A (such as OK); take a function #A : X ® P X such that, "a Î X,
#A(a) = { b
Î X | a
![]() A b
and b
A b
and b ![]() A
a }
A
a }
#A(a) is the 'A-equivalence class' of a, and a may be thought of as representing this class; indeed, b Î #A(a) iff #A(b) = #A(a), and so any member of #A(a)) may be used to represent that class. We are going to discuss algebraic structures whose elements will be, strictly speaking, such classes of wffs; where there is no danger of confusion, we shall simply represent such a class by one of its members; what we are doing is clearly an analog of the well-known use of Lindenbaum algebras in logic. Note that the grouping of wffs into classes defined by functions such as # may also be expressed in terms of a 'deductive identity' relation on X: for a, b Î X,
a =A b
iff a
![]() A
b and b
A
b and b
![]() A
a .
A
a .
Considering OK as our system, now, it is clear that OK's
![]() is reflexive (
is reflexive (![]() 1a) and transitive (
1a) and transitive (![]() 4); with identity based on equivalence classes as above, then,
4); with identity based on equivalence classes as above, then,
![]() OK
is a partial ordering and the 'deductive Lindenbaum structure' whose elements
are defined by #OK is a poset -- call it LOK.
Further,
OK
is a partial ordering and the 'deductive Lindenbaum structure' whose elements
are defined by #OK is a poset -- call it LOK.
Further, ![]() 1a and
1a and
![]() 3 give immediately:
3 give immediately:
| (1) | Kab
|
||
| (2) | Kab
|
Kab is then a lower bound of a and b in LOK. Also:
| (3) | a
|
||
| (4) | a, b
|
||
| (5) | a, b, g
|
Taking these last three sequents as premises for
![]() K gives:
K gives:
| (6) | Cab, Cag
|
With
| (7) | Cab
|
as a ![]() K premise in addition to
(6), we get
K premise in addition to
(6), we get
| (8) | CCabCag
|
Given (8), there is no problem in deriving
| (9) | If a
|
which establishes Kab as the greatest lower bound of a and b; LOK is then a meet semilattice.
Axioms N1, N2, and N3 make it easy to establish
| (10) | a
|
||
| (11) | a =OK NNa | ||
| (12) | Æ
|
||
| (13) | KaNNa =OK Æ |
These with what we already have make LOK an orthocomplemented lattice (OCL),
with Aab = NKNaNb
as join, and N as the orthocomplement. Since axiom OM will clearly make
the orthomodular identity provable, LOK is orthomodular;
![]() K, as we have noted, is characteristic for K's strict implicational
fragment; LOK will then have such an implication function
defined on it.
K, as we have noted, is characteristic for K's strict implicational
fragment; LOK will then have such an implication function
defined on it.
As we have noted, axiom CC might be stated
| (14) | PCabg |
which is to say that every implication is compatible with every g Î X, and so is center-valued in LOK . This axiom correlates nicely with certain properties of the semantics we shall present; that it is not a totally arbitrary postulate is indicated (as we shall see later) by the fact that in certain important extensions of OK -- viz., those containing S4's strict implicational fragment -- (14) is not optional, being provable directly from the implication postulates. Whether the center-valuation of implications is provable directly from K's strict implication postulates (making axiom scheme CC redundant) is an open question; my present conjecture is that it is provable, though I have not yet proven this.
The lattice LOK is a 'characteristic Lindenbaum lattice'
for OK in the sense that a
![]() OK
b iff #OK (a) < #OK(b)
in LOK . We now introduce a family of lattices associated with
any (sufficient-to-a-lattice) axiomatization A -- call this family 'Fam (A)'
. Each lattice in such a family will have classes of wffs of A as its elements
(as is the case with LOK ); supposing a
and b are any wffs of A and a and b
are classes of wffs belonging to a Lindenbaum lattice L , then, "a,
b e X:
OK
b iff #OK (a) < #OK(b)
in LOK . We now introduce a family of lattices associated with
any (sufficient-to-a-lattice) axiomatization A -- call this family 'Fam (A)'
. Each lattice in such a family will have classes of wffs of A as its elements
(as is the case with LOK ); supposing a
and b are any wffs of A and a and b
are classes of wffs belonging to a Lindenbaum lattice L , then, "a,
b e X:
If a
![]() A
b and a Î a and b
Î b, then
A
b and a Î a and b
Î b, then
a £ b in L iff L Î
Fam(A).
Fam(OK), then, is the class of all Lindenbaum OML's with K-strict implication defined on them and restricted to center-valuation. Fam(A) in any case may be called the "family of A-deductive lattice structures". From the definition of LOK and OK's postulates, it follows that
| (15) | G
|
It also will be the case that
| (16) | If G
Not-(#OK(g) £ #OK(a)), with g as in (15) |
Proof. Suppose that G
![]() OK a
fails; then by (15), #OK(g)
£ #OK(a)
fails
in LOK. But clearly, this last assertion fails in the smallest OM sublattice
L of LOK which has among its elements {#OK(b)
| b is a wf component of G,
a } (call this set Gen (L)), and which is closed under orthocomplementation.
Gen(L) is
the union of a set B(L) of sets of components of G, a each of which is a maximal (in
Gen(L)) set of mutually
compatible elements, and so defines a subset of one of the blocks of LOK -- Since Gen
(L) is finite, so too are
each of the xÎB(L). But each such x will
be a set of generators for one of the blocks of L (of which there also are a
finite number). Since a finite set of generators yields a finite Boolean algebra, each of the blocks of
L will be
finite, and so L as a composite of these blocks is finite, and is a finite member of
Fam(OK) in which
#OK(g)
£ #OK(a)
fails. This is the basis for the finite model property in OK, by the way.
OK a
fails; then by (15), #OK(g)
£ #OK(a)
fails
in LOK. But clearly, this last assertion fails in the smallest OM sublattice
L of LOK which has among its elements {#OK(b)
| b is a wf component of G,
a } (call this set Gen (L)), and which is closed under orthocomplementation.
Gen(L) is
the union of a set B(L) of sets of components of G, a each of which is a maximal (in
Gen(L)) set of mutually
compatible elements, and so defines a subset of one of the blocks of LOK -- Since Gen
(L) is finite, so too are
each of the xÎB(L). But each such x will
be a set of generators for one of the blocks of L (of which there also are a
finite number). Since a finite set of generators yields a finite Boolean algebra, each of the blocks of
L will be
finite, and so L as a composite of these blocks is finite, and is a finite member of
Fam(OK) in which
#OK(g)
£ #OK(a)
fails. This is the basis for the finite model property in OK, by the way.
OK and K (in K-N-C-strict) share the same set of wffs, X. For our purposes, a K-algebra is a Boolean Lindenbaum lattice with K-strict implication (or, equivalently, K necessity) defined on it; it is a member of Fam(K). Since K is an extension of OK, we have
| (17) | If G
|
Let us suppose, now, that the elements corresponding to G, a are an center-valued in LOK; we then have
| (18) | G
|
Proof: Only if, by (17); If: Suppose G
![]() OK a
fails; then by (16), $ a finite L Î
Fam(OK) in which Not-(#OK(g)
£ #OK(a)).
But by the center-valuation of G, a , L is
Boolean, and so is a K-algebra as well as a member of Fam(OK). This means
that G
OK a
fails; then by (16), $ a finite L Î
Fam(OK) in which Not-(#OK(g)
£ #OK(a)).
But by the center-valuation of G, a , L is
Boolean, and so is a K-algebra as well as a member of Fam(OK). This means
that G
![]() K a
also fails, q.e.d. for 'if'.
K a
also fails, q.e.d. for 'if'.
By the containment of OK in K we have:
| (19) | "a Î X, $b such that #OK(b) is center-valued in LOK and a =K b |
Proof: The addition of CKaANabb (Pab) to OK would extend that system to K; we may think of this schema as effecting a 'collapse' of all of LOK's blocks into its center by its assertion of universal compatibility; it leaves unchanged the relations between the elements of LOK's center, since they are already universally compatible. Its effect on each non-center-valued element of LOK would be -- by making such elements universally compatible -- to make it equivalent to some element of LOK's center, establishing (19).
Between (18) and (19) we have established:
| (20) | The center of LOK is a characteristic K-Algebra |
Indeed, it should be easy to see that:
| (21) | The Boolean B is a K-algebra iff it is isomorphic to a B' such that B' is the center of an L Î Fam(OK). |
Proof: only if: Immediate, since each K-algebra is in fact a member of Fam(OK), and may be considered the center of an OML that is 'all center'.
If: Suppose B' is the center of an L Î Fam(OK); since K-strict implication is defined on L, it is also defined on L's center, B', which is then a K-algebra by definition.
3. SEMANTICS FOR OK
The semantics for generalized normal logic will be based on the generalized
sample space (gss) of Foulis and Randall [1,
2] . Briefly, a gss is a space
whose member outcomes are not necessarily those of a single operation as is true
for classical sample spaces. A gss in [1] is a triple < W,
![]() ,
M(W)> with W the
set of 'outcomes' of the space,
,
M(W)> with W the
set of 'outcomes' of the space, ![]() a relation on
W such that, "x, y Î
W,
a relation on
W such that, "x, y Î
W,
| (22) | x |
||
| (23) | x |
x ![]() y may be read "x
is orthogonal to y" or "x and y are mutually
exclusive". M(W) is the 'manual of operations' or simply the 'manual' for the gss. The members of M(W) are intuitively interpreted as
the physical operations which can be executed to confirm or refute propositions
in the gss W; each such operation may be represented by and indeed may be
identified with the set of outcomes which executions of it can produce. W
is the entire set of outcomes involved, and so W = ÈM(W)
(classically, M(W) has one and only one member). If a g Í
W is such that "x, y Î
g, either x = y or x
y may be read "x
is orthogonal to y" or "x and y are mutually
exclusive". M(W) is the 'manual of operations' or simply the 'manual' for the gss. The members of M(W) are intuitively interpreted as
the physical operations which can be executed to confirm or refute propositions
in the gss W; each such operation may be represented by and indeed may be
identified with the set of outcomes which executions of it can produce. W
is the entire set of outcomes involved, and so W = ÈM(W)
(classically, M(W) has one and only one member). If a g Í
W is such that "x, y Î
g, either x = y or x ![]() y, then g is an orthogonal set; a maximal orthogonal set
f Í W is an orthogonal set
such that "x Î
W, x Ï f implies that $
y Î f such that not-(x
y, then g is an orthogonal set; a maximal orthogonal set
f Í W is an orthogonal set
such that "x Î
W, x Ï f implies that $
y Î f such that not-(x
![]() y). Each operation in M(W)
is maximal orthogonal in W. The postulates for gss's in [1] permit
certain spaces to have maximal orthogonal sets which are not operations of M(W);
let us simplify this somewhat and specify that each maximal orthogonal set of W
is an operation of M(W) -- this is the condition that Foulis and Randall
call 'complete coherence' of W. For our purposes we lose nothing by
assuming complete coherence, since any gss which is not completely coherent can
be extended to a completely coherent gss by supplementing the manual with
operations corresponding to each of its maximal orthogonal sets. So we may think
of a gss as a pair <W, M(W)>, W and M(W) as
before, and
y). Each operation in M(W)
is maximal orthogonal in W. The postulates for gss's in [1] permit
certain spaces to have maximal orthogonal sets which are not operations of M(W);
let us simplify this somewhat and specify that each maximal orthogonal set of W
is an operation of M(W) -- this is the condition that Foulis and Randall
call 'complete coherence' of W. For our purposes we lose nothing by
assuming complete coherence, since any gss which is not completely coherent can
be extended to a completely coherent gss by supplementing the manual with
operations corresponding to each of its maximal orthogonal sets. So we may think
of a gss as a pair <W, M(W)>, W and M(W) as
before, and ![]() derived from M(W). We
further specify, by the way, that the gss's we deal with are such that all their
operations are countable in size.
derived from M(W). We
further specify, by the way, that the gss's we deal with are such that all their
operations are countable in size.
We shall state here some terminology and a number of facts about gss's. Where
needed, proofs will be found in [1] . Since the x Î
W confirm and refute propositions, each a Í
W is called an evidence set; if an evidence set a Í
g, with g an operation (i.e., g Î
M(W)), a is called an event, specifically, an event for W; note
that this terminology is more general than that of classical sample spaces,
where every evidence set is an event. A function
![]() :
PW ® PW
is definable on the
gss, based on the relation
:
PW ® PW
is definable on the
gss, based on the relation ![]() and such that, "a Í
W,
and such that, "a Í
W,
| (24) | a |
a![]() is then the set of all outcomes orthogonal to everything in
a. Based only
on (22)-(24), a number of properties of
is then the set of all outcomes orthogonal to everything in
a. Based only
on (22)-(24), a number of properties of ![]() are statable (proofs in [1] ):
are statable (proofs in [1] ):
| (25) | a Ç a |
||
| (26) | a Í
a |
||
| (27) | a |
||
| (28) | If a Í
b then b |
On an intuitive level, ![]() behaves very much like classical negation; in general, however, a = a
behaves very much like classical negation; in general, however, a = a![]()
![]() does not hold. If we do have an a for which a = a
does not hold. If we do have an a for which a = a![]()
![]() ,
we say that a is a closed subset or subspace of W. In fact, the set of
closed subspaces of any gss is an orthocomplemented lattice (OCL), with set
intersection as meet (a Ù b)
and
,
we say that a is a closed subset or subspace of W. In fact, the set of
closed subspaces of any gss is an orthocomplemented lattice (OCL), with set
intersection as meet (a Ù b)
and ![]() as orthocomplement. Call W's
set of closed subspaces Cl(W); Cl(W) is not in general closed
under unions; however, taking a Ú b
as (a
as orthocomplement. Call W's
set of closed subspaces Cl(W); Cl(W) is not in general closed
under unions; however, taking a Ú b
as (a![]() Ç
b
Ç
b![]() )
)![]() which is (a È b)
which is (a È b)![]()
![]() supplies us with our join function.
supplies us with our join function.
Let us insert example 1 at this point. Take our gss as
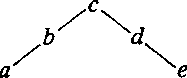
This is the 'Greechie representation' of a particular gss, and indeed of the associated lattice. W is <a, b, c, d, e> and M(W) is given by the arrangement -- outcomes on a line with each other belong to the same operation and so are orthogonal to each other; the maximal orthogonal sets then are <a, b, c> and <c, d, e>; Computation of Cl(W) here gives twelve closed subsets, which comprise the lattice known as L12:
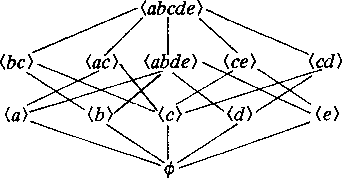
This is an OML whose center is {<a b c d e>, <a b d e>, <c>, Æ} and whose blocks are Boolean {23} corresponding to the respective operations in the gss.
Under certain circumstances (those which, in fact, interest us most), Cl(W) is orthomodular as well as orthocomplemented. Such W are called "conjunctive Dacey spaces" by Foulis and Randall. A slight divergence (of which more later) between my approach and theirs leads me to call such spaces 'symmetric' after the symmetry of compatibility
| (29) | EPabPba |
which is characteristic of OML's. The following theorem gives a necessary and sufficient condition that W be symmetric; first, let us note that a maximal subevent of a set a a Í W will be the intersection of a with an operation, i.e., a set maximal orthogonal in a:
| (30) | W is a symmetric space (i.e., Cl(W) is an
OML) iff "a |
Proof: Only if: Suppose a![]()
![]() and d as above, but suppose further that a
and d as above, but suppose further that a![]()
![]() ¹ d
¹ d![]()
![]() .
We then have d
.
We then have d![]()
![]() Ì a
Ì a![]()
![]() and so a
and so a![]() Ì
d
Ì
d![]() ,
both properly; thus $ f disjoint from d
,
both properly; thus $ f disjoint from d![]()
![]() such that a
such that a![]()
![]() = d
= d![]()
![]() È f. Since d is maximal
orthogonal in a
È f. Since d is maximal
orthogonal in a![]()
![]() ,
no members of d
,
no members of d![]() can appear in f -- and obviously, none can be in d
can appear in f -- and obviously, none can be in d![]()
![]() .
This then gives us a
.
This then gives us a![]()
![]() Ç d
Ç d![]() = (d
= (d![]()
![]() È f) Ç
d
È f) Ç
d![]() = Æ.
This is what is required to make the subset
= Æ.
This is what is required to make the subset
<W, d![]() ,
a
,
a![]() , d
, d![]()
![]() ,
a
,
a![]()
![]() ,
Æ>
,
Æ>
a sublattice. But this lattice is the 'benzene ring'; as is well-known, having the benzene ring as a sub-OC sublattice is a necessary and sufficient condition that an OCL be non-OM; Cl (W) is then non-OM and so W is not symmetric. Contraposition gives 'only if'.
If. Suppose a![]()
![]() and d as above, " such a, d , with
a
and d as above, " such a, d , with
a![]()
![]() = d
= d![]()
![]() .
If, then, an event h Í a
.
If, then, an event h Í a![]()
![]() is such that h
is such that h![]()
![]() ¹ a
¹ a![]()
![]() ,
h is not maximal orthogonal in a
,
h is not maximal orthogonal in a![]()
![]() ,
and so we have a
,
and so we have a![]()
![]() Ç h
Ç h![]() ¹ Æ.
This means that <W, d
¹ Æ.
This means that <W, d![]() ,
a
,
a![]() , d
, d![]()
![]() ,
a
,
a![]()
![]() ,
Æ> fails to be a sublattice; this may be
extended by induction to all subsets g of a
,
Æ> fails to be a sublattice; this may be
extended by induction to all subsets g of a![]()
![]() such that g
such that g![]()
![]() ¹ a
¹ a![]()
![]() . a
. a![]()
![]() can then be the shoulder of no benzene ring sublattice. Having a shoulder of the
benzene ring (as a subset of an OCL) be a non-event is a necessary condition
that that subset be a sublattice (consider the benzene ring):
can then be the shoulder of no benzene ring sublattice. Having a shoulder of the
benzene ring (as a subset of an OCL) be a non-event is a necessary condition
that that subset be a sublattice (consider the benzene ring):
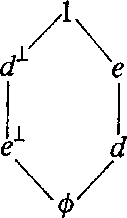
Suppose that d![]() and e are
both events; e
and e are
both events; e![]() and d also must be events; this makes e È
e
and d also must be events; this makes e È
e![]() orthogonal
and so maximal orthogonal; and any x Î
d
orthogonal
and so maximal orthogonal; and any x Î
d![]() , Ï
e
, Ï
e![]() , since it
must be orthogonal to all in e
, since it
must be orthogonal to all in e![]() ,
must also be in e; if e
,
must also be in e; if e![]() ¹ d
¹ d![]() ,
then, e
,
then, e![]() Ç
d ¹ Æ,
and the benzene ring is not a sublattice). Since this holds for all non-events
in the set of closed subsets of W we conclude that there are no benzene
ring sublattices, and so we conclude that Cl(W) is OM, and so W is
a symmetric space.
Ç
d ¹ Æ,
and the benzene ring is not a sublattice). Since this holds for all non-events
in the set of closed subsets of W we conclude that there are no benzene
ring sublattices, and so we conclude that Cl(W) is OM, and so W is
a symmetric space.
The gss may be thought of as a 'locus' for confirming and refuting
propositions; in fact, we call a proposition well-defined (with respect to a
given gss) if its precise conditions of confirmation and refutation are given;
from the semantical point of view, a well-defined proposition may be identified
with an ordered pair <a, b> where a is the confirming and b
the refuting evidence set for that proposition. Obviously, assumptions as to
what a and b are will have a critical effect on the semantics
being studied. We follow Foulis and Randall in specifying that the confirming
and refuting evidence sets associated with propositions will be closed, and that
the refuting set will be the ![]() of the confirming set (see [1] for details). Thus if a is the evidence
set confirming proposition a, we may say that a
of the confirming set (see [1] for details). Thus if a is the evidence
set confirming proposition a, we may say that a![]()
![]() effectively or virtually confirms a, and will
semantically identify a with <a
effectively or virtually confirms a, and will
semantically identify a with <a![]()
![]() ,
a
,
a![]() >. Note
that this procedure has as a limiting case the association, in classical ss's,
of propositions with events; as the set of 'perational propositions' for a
classical space is isomorphic to the set of 'observable events' in the Boolean
subset algebra of the space, so too does our approach associate the set of
propositions for a gss with the lattice of closed subspaces of that space. Note
that with a proposition being <a
>. Note
that this procedure has as a limiting case the association, in classical ss's,
of propositions with events; as the set of 'perational propositions' for a
classical space is isomorphic to the set of 'observable events' in the Boolean
subset algebra of the space, so too does our approach associate the set of
propositions for a gss with the lattice of closed subspaces of that space. Note
that with a proposition being <a![]()
![]() ,
a
,
a![]() >, we may
always compute the refuting set given the confirming, and so may simply identify
(semantically) each proposition with its confirming evidence set. In what
follows, we shall use [a] to represent
the closed evidence set confirming the proposition a;
obviously, [a] may be considered to
represent an equivalence class, of the propositions semantically equivalent to
a. We shall discuss the precise conditions of confirmation and refutation of
propositions shortly, when we have introduced the concept of the generalized
frame.
>, we may
always compute the refuting set given the confirming, and so may simply identify
(semantically) each proposition with its confirming evidence set. In what
follows, we shall use [a] to represent
the closed evidence set confirming the proposition a;
obviously, [a] may be considered to
represent an equivalence class, of the propositions semantically equivalent to
a. We shall discuss the precise conditions of confirmation and refutation of
propositions shortly, when we have introduced the concept of the generalized
frame.
A point worth noting here is a difference between the approach of Foulis and Randall [1, 2] and the present. When Foulis and Randall discuss 'logics' associated with their gss's, they limit themselves to propositions whose confirming evidence sets are the 'closures' of events, while I wish to consider propositions corresponding to all closed evidence sets. The difference in approach is evinced in such gss's as Janowitz's: (example 2)
Here <a, e> and <c, g> are closed subsets which are
the closures of no events. The set of closed subsets of example 2 is an OCL, but
if these last two mentioned subsets are eliminated from it, the result is not a
lattice, but an OM poset lacking joins for the pairs <<a>, <e>>
and <<c>, <g>> and also the dual meets. The
claim has been made that the admission of such posets as logics is useful since
it relieves us of the need to supply interpretations for the conjunctions and
disjunctions of certain pairs of incompatible assertions. However, it has not
been noticed, apparently, that the use of a non-lattice poset as a logic itself
introduces certain basic embarrassments: viz: since such posets are not
closed under meet and join, the sets of propositions corresponding to them are
not closed under conjunction and disjunction. Sacrificing the integrity of the
set of wffs is too high a price to pay for the elimination of certain
'embarrassing' propositions. The propositions represented by <a, e>
and <c, g> in the space in question are untestable in a
well-defined sense: a proposition is testable (in a gss W) if its
(closed) confirming set a is such that e Í
a È a![]() ,
with e an operation in M(W). Now, untestable propositions are
somewhat awkward and even pathological, perhaps, but they are not unutterable,
which is the status they are consigned to in the Foulis and Randall approach. To
say that a is untestable is to say something important about it.
,
with e an operation in M(W). Now, untestable propositions are
somewhat awkward and even pathological, perhaps, but they are not unutterable,
which is the status they are consigned to in the Foulis and Randall approach. To
say that a is untestable is to say something important about it.
Happily, the Foulis and Randall approach and ours produce the same results at a key point -- when the spaces involved are symmetric; the earlier proven theorem (30) establishes this: every closed subspace of a symmetric space is the closure of an event, and so for such spaces, the Foulis and Randall admissible logics are the same as ours.
4. THE GENERALIZED FRAME
As we have noted, Cl(W) will be the lattice of closed subspaces of W; we will be working with symmetric W, and let us name the center of Cl(W) Cen (W). We shall also specify a subset of Cen(W) as follows:
QW = { h Î Cen(W) | h covers Æ in Cen(W) }
Cen(W) is a sub-OC Boolean sublattice of C1(W), which is an atomic OML; this means that QW will be the set of atoms of Cen(W) when that lattice is considered by itself; call QW the set of quasi-atoms of Cen (W). With h Î QW, consider the OM ideal in Cl(W) which has h as its unit; call this lattice Ih; the following then obtain:
| (31) | Ih is a trivial-centered OML, "h Î QW. | ||
| (32) | The lattice-theoretical product of the members of { Ih | h Î QW } is Cl(W), and each finite OML may be represented as such a product. |
We may take (31) as obvious; note that if Cl(W) itself is irreducible, the only member of Qw is W. (32) is essentially proven in [5, p. 75] .
Each h E Qw is a set of outcomes which in turn divides into one or more sets maximally orthogonal in h, given M(W). Based on this division of such h into maximal orthogonal sets - we shall specify that this information is part of the definition of QW - we may think of each h E Qjy as itself being a sample space with its own manual of operations; indeed, it is clear that:
| (33) | For each h Î QW, Ih = Cl(h). |
Now consider two manuals M(X) and M(Y) for symmetric spaces. Form the Cartesian product of these manuals, and consider
{ Èg | g Î M(X) ´ M(Y) },
the set of unions of members of that product. As each member of this set is a set of outcomes, this set itself is a manual of operations; call it MXY, and refer to it as "the product manual of M(X) and M(Y)". Then:
| (34) | Assuming symmetric spaces, the lattice-theoretical product Cl(X) ´ Cl(Y) is the lattice Cl (ÈMXY). |
Proof: Each h Î
Cl(X) ´ Cl(Y) is representable as a union r
È s where r Î
Cl(X)
and s Î
Cl(Y); clearly, each such r È s is a subset of
ÈMXY, and all such r È
s
are among those subsets. Let ![]() x and
x and
![]() y be the orthocomplement functions relative
to X and Y respectively, and
y be the orthocomplement functions relative
to X and Y respectively, and ![]() the OC relative to the product lattice. Suppose
first that r È s Î
Cl(ÈMXY), for r Í
X, s S Í Y. Since r
the OC relative to the product lattice. Suppose
first that r È s Î
Cl(ÈMXY), for r Í
X, s S Í Y. Since r![]() = r
= r![]() x È
Y, the closed
nature of r È s implies that r is closed in
X; similarly for s in Y, and we have
r Î
Cl(X), s Î
Cl(Y). On the other hand, assume r Î
Cl(X), s Î
Cl(Y), and
compute (r È s)
x È
Y, the closed
nature of r È s implies that r is closed in
X; similarly for s in Y, and we have
r Î
Cl(X), s Î
Cl(Y). On the other hand, assume r Î
Cl(X), s Î
Cl(Y), and
compute (r È s)![]()
![]() . This is
(r
. This is
(r![]() Ç
s
Ç
s![]() )
)![]() , which
in turn is
, which
in turn is
((r![]() x È
Y) Ç (s
x È
Y) Ç (s![]() y
È X))
y
È X))![]() =
=
(r![]() x È
Y)
x È
Y)![]() È
(s
È
(s![]() y È
X)
y È
X)![]() =
=
((r![]() x)
x)![]() Ç X) È
((s
Ç X) È
((s![]() y)
y)![]() Ç Y) =
Ç Y) =
((r È Y) Ç
X) È ((s È
X) Ç Y) =
r È s.
Such r È s are then closed in ÈMXY, and (34) is established. It then follows that:
| (35) | The product manual of all the h Î QW is M(W), and so the lattice of closed subspaces defined by it is Cl(W). |
We then see that given QW we can determine M(W) (and vice-versa, of course); we may then replace M(W) in the representation of a sample space by QW (assuming the members of QW to be labeled as to their maximal orthogonal sets, of course). Each of the members h of QW is then itself a sample space; the product manual of the manuals of the members of QW is M(W), and the product of the lattices associated with the members of QW (which are all irreducible) is Cl(W); in the generalization of the classical modal frame we are about to set out, the members of QW are analogs of the 'points' or 'possible worlds' of the classical frame. It also follows that each manual and its associated OML are 'factorable' into the appropriate QW and trivial-centered OML's corresponding to the members of QW. As an example, the manual of example 1 factors to the following two manuals:
< a¾b d¾e > and < c >
whose product as indicated above is the manual of example 1; the lattices of closed subspaces of these sample spaces are
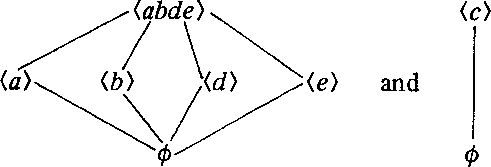
whose product is indeed L12, the lattice associated with the space of example 1.
Then, let < W, QW > be a gss; we shall then call < W, QW, R > a generalized normal frame (gnf); R is a relation on QW; as we have noted, this makes QW analogous to the set of possible worlds in a classical frame. In the case in which the space in question is classical, we have W = QW -- or, more precisely, QW is the set of singleton sets of W's members; we note in passing that the gnf thus provides us with a conceptual nexus between classical probability theory and the semantics of classical modal logic.
With a gnf as above, call < W, QW, R , v > = M a model on the gnf W, with v : { atomic formulas } ® Cl(W). v may be called a, 'valuation', and v(p) may be thought of as designating the closed evidence set whose member outcomes confirm p at the model in question. In the classical analog of such a model, v(p) is usually thought of as designating the set of possible worlds at which p is true; because of the virtual identity of W and QW classically, designating the confirming evidence set and designating the 'worlds at which p is true' is, classically, essentially the same thing.
Given a model M and any wff a, we shall designate the closed set of outcomes confirming a by [a]M; in most cases there will be no doubt as to which model we are referring to, and so we will ordinarily drop the subscript M . What we are about to do now is to state precise conditions of confirmation for the propositions in X, in effect to semantically 'well-define' these propositions in the sense of Foulis and Randall. [a] for any a is determined as follows: |
| Where p is any atomic formula, [p] = v(p) | |||
| [Kab] = [a] Ù [b] | |||
| [Na] = [a] |
|||
| [Cab] = È{ h Î QW | "g(Rhg implies [a] Ù g £ [b] |
Note that although Cl(W) is not, in the general case, closed under set-theoretical union, Cen(W) is so closed. The set of elements whose union is [Cab] is a subset of Cen(W), and so
| (36) | [Cab] Î Cen(W), " a, b Î X |
[Eab] , [Aab], and [La] may be computed employing the appropriate definitions.
Intuitively speaking, Cab is evaluated at a given h Î Cen(W) -- at a given possible world -- by examining the members of QW to which h 'has access' as given by the relation R . If the set of outcomes at each such possible world confirming a is included in the set of outcomes confirming b, then Cab 'holds' at h -- in the sense that it is confirmed by every outcome belonging to h; [Cab] is then the total set of outcomes at possible worlds at which Cab holds. Clearly, this definition is a generalization of the semantic definition of 'strict implication' in classical normal frames.
5. THE COMPLETENESS OF OK
Based on the previous section, we may define semantic entailment: write G ®W a and say "the formulas G semantically entail a" or "the argument from G to a is valid" in the gnf <W, QW, R> iff $ no model for that gnf in which all of the G are confirmed while a is refuted; when G is empty, this will mean that a is confirmed in all models for that gnf. The simple G ® a will mean that the argument from G to a is valid in all gnf's. It is clear that:
| (37) | Where g is the
conjunction of the G , or is 1 where G
is empty, G ® a iff [g] Í [a] for every model for every gnf. |
Now, note that if a ®W b and b ®W a, then [a] = [b] in every model for W; we may then consider [a] to be the equivalence class for W of formulas semantically equivalent to a. Under this interpretation, and since Cl(W) is an OML, we have immediately:
| (38) | [Cab] Î Cen(W), " a, b Î X |
Now, consider a finite lattice L Î Fam(OK). Let WL be the set of atoms of L. Each of the quasi-atoms of L's center is representable as a join of one or more members of WL ; let QL be the set of quasi-atoms so represented. By (21), the center of L is a K-algebra, and so is associated with an accessibility relation R defined on the classical frame associated with that K-algebra. It is clear that <WL, QL, R> is a (finite) gnf. Thus we have
| (39) | For all finite L Î Fam(OK), L = Cl(WL), where <WL, QL, R> is a gnf. |
So, by (38) and (39):
| (40) | The classes of finite members of Fam(OK) and of finite gnf's are isomorphic. |
We then have, by (40), (37), and (16):
| (41) | If G
|
This is a completeness result for OK with respect to the class of gnf's.
It would be elementary to show that all the axioms of OK are valid in all gnf's, and that validity is hereditary through OK's rules of inference. This gives (41)'s converse, and so
| (42) | G
|
6. EXTENSIONS OF OK
Clearly, OK may be extended in a variety of ways. Changing rule
![]() 4 to the form
4 to the form
|
makes La
![]() a
provable (Clp
a
provable (Clp
![]() 1 and Clp
1 and Clp
![]() Clp are both OK provable; take these as premises for
Clp are both OK provable; take these as premises for
![]() 4'). Call OK with this rule OT; this system will correspond to the
class of gnf's in which R is reflexive just as OK does to
the entire class of gnf's. We may also extend OK and OT by
supplementing or replacing
4'). Call OK with this rule OT; this system will correspond to the
class of gnf's in which R is reflexive just as OK does to
the entire class of gnf's. We may also extend OK and OT by
supplementing or replacing ![]() K. Adding
K. Adding
| If a, G
|
to OT gives OS4, whose class of gnf's is transitive and reflexive so far as R is concerned. Alternatively, formulate OS4 by replacing the distributive law in Hacking's S4 of [10] by axiom OM.
Now note that
| (43) | .Cag
|
is easily provable in OK; take a as NCab; this gives
| (44) | .CNCabg
|
The formula
| (45) | CCabCNgCab. |
is provable given S4's strict implication; with OK's N axioms this gives
| (46) | .CCabCNCabg |
which with (44) gives
| (43) | .Cab
|
This is here equivalent to axiom CC. Thus, the center-valuation of implication in OS4 is not optional and CC is there redundant.
It should be clear that OK may be extended to other normal systems as well, by adding postulates sufficient to the pure strict implications of those systems; as established in [9] , modularity (and so distributivity) is not forced to hold by the extension of an OML by any of the strict implications included in S5.
7. EMPIRICAL INTERPRETATIONS
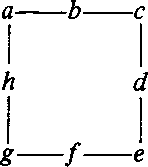
We shall conclude by briefly suggesting how the gnf may be used to provide empirical interpretations for normal implications. Foulis and Randall [1, 2] suggest that we consider a 'particle emitting device'; associated with this is a gss whose manual may be diagramed:
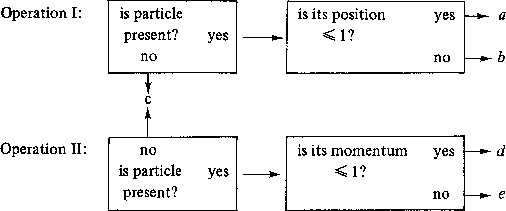
The outcomes, say, 'printed' by the operations in this manual are a, b, c, d, and e; this space may also be represented

This is the gss of example 1, which gives the OML L12. As we have noted, this manual 'factors' into the two manuals
< a¾b d¾e > and < c >
Note that each of these factor manuals corresponds to a different stage in the operations of the manual in its 'flow chart' representation; <c> is the "is particle present?" stage, and <a¾b d¾e> the (composite) position check/momentum check stage. Thus the 'possible worlds' of the gnf's associated with this gss are determined by the stages of the flow chart diagramming the manual. This gives natural interpretations to R, the 'accessibility relation' on these gnf's. One such interpretation would be to read Rxy as "stage x precedes or is the same as stage y", or "y is 'realizable from' x". This R 'follows the arrows' in the flow chart. An alternative interpretation would be to read Rxy as "information secured at stage y of the manual is available at stage x"; this reading looks in the opposite direction from the first; here stages in the past are accessible to those later on. The values of the implications definable on the associated lattices will differ accordingly, though the center of each will be a characteristic K4 algebra (K4 = S4 + CpCMLpLp + CLMpMLp -- see [8, pp. 268-71] ). It is clear that other interpretations are possible; the key thing is to note that the gnf permits the association of implication with the 'flow' of the manual of operations, and so provides an empirical interpretation of normal implications defined on OML's, albeit one more complex than that of conjunction, disjunction, and negation.
University of Florida
Gainesville, Florida