Peirce and Philo*
Jay Zeman
Charles Peirce, logician and philosopher, contributed
notably to the theory of the conditional. Actually, from his perspective and in his
terminology it is better, as we shall see, to link his work on the conditional with
his discussions of the hypothetical proposition. Peirce spoke often of the consequentia
de inesse,1 the concept of which is intimately linked
with the material, or "Philonian" conditional; indeed, we shall see him calling
himself a Philonian. And it is not uncommon to hear Peirce—at least prior to the last
decade of his life—declared a Philonian, whose fundamental analysis of the
conditional was essentially the same as that of Philo (and of more modern types like
Russell and like Quine).
In this paper, I intend first to examine
Peirce’s understanding of "Philonian"; I will then look at the Philonian or
"de inesse" conditional in the context of his overall logical thought. It
is commonly held that Peirce in his early years held to the "nominalistic"
Philonian conditional, and only later "surrendered" it in favor of a more
"realistic" view; the study we are here undertaking will indicate that this does
not adequately reflect his position.
As we shall see, Peirce at one time or another called
himself a Philonian. He was, of course, also quite aware that Philo is historically paired
with his teacher Diodorus. That pairing, in fact, is so integral to the meaning of
"Philonian" that without consideration of it, "Philonian conditional"
becomes a somewhat pretentious term for "truth-functional implication,"
When he discusses the historical pairing I have
mentioned, Peirce employs "Diodoran" as the adjective derived from the name of
Diodorus. Our considerations here are complicated by contemporary discussions; an index of
the complication is the fact that the usual contemporary form of the adjective is
"Diodorian." Arthur Prior, one of the rediscoverers of the possible worlds
approach to modal logic,2 used Diodorus as a take-off point
in his work (see Prior 1955, 1957); Prior, and modal logicians
following him, employed this latter form of the relevant adjective. Prior at first thought
that what he called the "Diodorian modal system" supplied semantics for S4; this
misapprehension was rather quickly dispelled, however, and ‘Diodorian modality’
gravitated to its contemporary usage: generically, it means the class of modal logics with
reflexive, transitive, and linear (total-ordered) relational frames (that is, the
systems containing S4.3); specifically, it refers to one of these systems, "D,"
the system in whose frames "possible worlds" are "discrete" (see Zeman 1973).
Peirce’s discussions of the Philo-Diodorus
debate are among those in which he anticipates the discovery of possible-worlds modal
semantics; we must not, however, conclude that his term "Diodoran" means
anything like the contemporary "Diodorian." We find him saying that
Cicero informs us that in his time there was a famous
controversy between two logicians, Philo and Diodorus, as to the signification of
conditional propositions. Philo held that the proposition "if it is lightening it
will thunder" was true if it is not lightening or if it will thunder and was only
false if it is lightening but will not thunder. Diodorus objected to this. Either the
ancient reporters or he himself failed to make out precisely what was in his mind, and
though there have been many virtual Diodorans since, none of them have been able to state
their position clearly without making it too foolish. Most of the strong logicians have
been Philonians, and most of the weak ones have been Diodorans. For my part, I am a
Philonian; but I do not think that justice has ever been done to the Diodoran side of the
question. The Diodoran vaguely feels that there is something wrong about the statement
that the proposition, "If it is lightening it will thunder," can be made true
merely by its not lightening (NEM 4:169; this is MS 441 (1898)).
Although Peirce comments elsewhere that "the Diodoran
view seems to be the one which is natural to the minds of those, at least, who speak the
European languages" (CP 3.441), he takes (as is suggested above) a rather dim view of
those who have advocated this position. He contrasts the Philonian and Diodoran positions
thus:
According to the Philonians, "If it
is now lightening it will thunder," understood as a consequence de inesse,
means "It is either not now lightening or it will soon thunder." According to
Diodorus, and most of his followers (who seem here to fall into a logical trap), it means
"It is now lightening and it will soon thunder" (CP 3.442).
Far from being connected with the contemporary
"Diodorian" modal logic (which, from an important perspective, fits perfectly
within Peirce’s own theory of possibility), the Diodoran position as understood by
Peirce seems to require a sort of "existential import" for the antecedent
condition (in the above case, "It is now lightening"). A function with the
meaning ascribed above by Peirce to the conditional of "Diodorus, and most of his
followers," is, of course, not really a conditional, but is much closer in meaning to
a conjunction. This won’t do, but Peirce is unwilling simply to reject the
"Diodoran" strategy. Presumably, this approach expresses something about
the conditional that can be taken as common-sense wisdom about it; perhaps Peirce himself
can come to the aid of the inept Diodoran, and can
fit him out with a better defence than he has
ever been able to construct for himself, namely, that in our ordinary use of language we
always understand the range of possibility in such a sense that in some possible case the
antecedent shall be true (NEM 4:169).
Taken thus, the "Diodoran" position is not
really in competition with the Philonian, but might be considered complementary to
it, reflecting something to do with ordinary uses of language.
This sense of "Diodoran" stands in contrast to
the technical modal "Diodorian" of the last couple of decades: Peirce’s
reading of Diodorus is quite different from Prior’s. And Peirce’s understanding
of Philo/Diodorus also differs from another way in which these Ancients may be compared.
It is possible to see Philo vs. Diodorus as the preliminary bout of a card of
fights which has more recently matched C. I. Lewis with the Russellians and W. v. O. Quine
with Ruth Marcus. The most visible issue in the disputes I mention here is that of the
nature of modal propositions, and in particular, of the relationship of
"implication" to modality. In the terminology of Lewis, this is the question of
"material" vs. "strict" implication. And in terminology often
used in discussing broad movements in western philosophy, it is the matter of
"nominalism" vs. "realism." Peirce’s understanding of
Philo vs. Diodorus does not seem, as our quotes indicate, to reflect this contrast.
I emphasize this so that we won’t unconsciously read current approaches back into
Peirce.
Now, it is generally accepted that a development can be
traced over the years in Peirce’s thought. As one commentator has put it,
Peirce’s philosophy is like a house
which is being continually rebuilt from within. Peirce works now in one wing, now in
another, yet the house stands throughout, and in fact the order of the work depends upon
the house itself since modification of one part necessitates the modification of another.
And although entire roofs are altered, walls moved, doors cut or blocked, yet from the
outside the appearance is ever the same (Murphey 4).
Well, perhaps; I think that it is well to examine
carefully the extent to which "modifications" actually occur, however. The
richness of a later position may not at all mean that its earlier forebears have been
abandoned. It may be that these earlier positions are, in fact, so well established as to
be unproblematic with respect to the later position; three decades after the Illustrations
of the Logic of Science series, for example, Peirce was writing expansive
footnotes on those papers—but hardly rejecting Pragmatism as laid out there.
Now, coming near matters which will be near to our concern
here, in tracing "Peirce’s Progress from Nominalism to Realism," another
author tells us that
Since the proof of pragmaticism, and
thereby of realism, can be most cogently stated in existential graphs, the series [of Monist
articles beginning in 1905] proceeds to a fresh exposition of the graphs (CP 4.530-572).
But the Monist printer’s ink is scarcely dry on that when Peirce hits
upon an improvement to enable them to represent different kinds of possibilities; and,
confronted by this improvement, his other self, his nominalist self, surrenders his last
stronghold, that of Philonian or material implication (Fisch 1986).3
CP 4.546 is even more difficult to see as the
"surrender of [a] stronghold," although its emphasis is on the reality of
possibles (see my discussion of the EG rule given in CP 4.569; the "suiciding
wife" example is connected to this, and it is further discussed in CP 4.580).
Actually, a fairly careful study of material available
from the period in which this "surrender" is supposed to have taken place
doesn’t give much evidence of it; in fact, there is at this period very little
testimony of concern with the conditional as such. Now I certainly don’t believe that
a dearth of discussions specifically regarding the conditional indicates that Peirce had
lost interest in it. I believe, rather, that Peirce’s theory of the conditional had
taken its basic form long before, and that while there would be elaborations and
amplifications of that theory, that basic form—which was integral to his
thought—would maintain itself intact.
My own investigations lead me to believe that
Peirce’s relationship to the Philonian conditional is quite complex; although there
was an increased emphasis on the reality of thirds and firsts in the later Peirce, his
view of the conditional de inesse sees it as second to a larger third from about
the days of the Illustrations of the Logic of Science, anyway.
I note that in many locations Peirce speaks not of conditional
propositions, but of hypotheticals. The term "hypothetical" suggests a
strong link between mathematical logic and philosophy for Peirce; we note its role in the
thought of Kant, for example, who was a major influence on Peirce, while on the other
hand, seeing that Peirce’s discussions of "hypotheticals" are almost always
located in the context of his symbolic logic. Let’s look at what he says in the
well-known Philosophy of Notation article of 1885:
To make the matter clear,
it will be well to begin by defining the meaning of a hypothetical proposition, in
general. What the usages of language may be does not concern us; language has its meaning
modified in technical logical formulae as in other special kinds of discourse. The
question is what is the sense which is most usefully attached to the hypothetical
proposition in logic? Now the peculiarity of the hypothetical proposition is that it goes
out beyond the actual state of things and declares what would happen were things
other than they are or may be. The utility of this is that it puts us in possession of a
rule, say that "if A is true, B is true," such that should we
hereafter learn something of which we are now ignorant, namely that A is true,
then, by virtue of this rule, we shall find that we know something else, namely, that B
is true. There can be no doubt that the Possible, in its primary meaning, is that which
may be true for aught we know, that whose falsity we do not know.4
The purpose is subserved, then, if throughout the whole range of possibility, in every
state of things in which A is true, B is true too. The hypothetical
proposition may therefore be falsified by a single state of things, but only by one in
which A is true while B is false. States of things in which A is
false, as well as those in which B is true, cannot falsify it. If, then, B
is a proposition true in every case throughout the whole range of possibility, the
hypothetical proposition, taken in its logical sense, ought to be regarded as true,
whatever may be the usage of ordinary speech. If, on the other hand, A is in no
case true, throughout the whole range of possibility, it is a matter of indifference
whether the hypothetical be understood to be true or not, since it is useless. But it will
be more simple to class it among true propositions, because the case in which the
antecedent is false do not, in any other case, falsify a hypothetical. This, at any rate,
is the meaning which I shall attach to the hypothetical proposition in general, in this
paper (CP 3.374).
I note especially in the above Peirce’s speaking of
"a proposition true in every case throughout the whole range of possibility";
the notion of quantification over a range of possibility is central here. And we see him
in 1902 saying that
the quantified subject of a hypothetical
proposition is a possibility, or possible case, or possible state of
things. In its primitive state, that which is possible is a hypothesis which in
a given state of information is not known, and cannot certainly be inferred, to be false.
The assumed state of information may be the actual state of the speaker, or it may be a
state of greater or less information. Thus arise various kinds of possibility (CP 2.347).
The notion of quantification over a range of possibilities
is a basic theme in Peirce’s work; in 1902, he himself sees his understanding of
hypotheticals in these terms as going back even earlier than the Philosophy of Notation
paper:
In a paper which I published in 1880, I
gave an imperfect account of the algebra of the copula. I there expressly mentioned the
necessity of quantifying the possible case to which a conditional or independential
proposition refers. But having at that time no familiarity with the signs of
quantification which I developed later, the bulk of the chapter treated of simple
consequences de inesse. Professor Schröder accepts this first essay as a
satisfactory treatment of hypotheticals; and assumes, quite contrary to my
doctrine, that the possible cases considered in hypotheticals have no multitudinous
universe. This takes away from hypotheticals their most characteristic feature (CP 2.349).
Peirce probably refers here to the well-known paper of CP
3.154 ff.; he notes there that
De Morgan, in the remarkable memoir with
which he opened his discussion of the syllogism . . . has pointed out that we
often carry on reasoning under an implied restriction as to what we shall consider as
possible, which restriction, applying to the whole of what is said, need not be expressed.
The total of all that we consider possible is called the universe of discourse, and
may be very limited. One mode of limiting our universes by considering only what actually
occurs, so that everything which does not occur is regarded as impossible (CP 3.174).
And a universe so limited would be, of course, the
universe of the de inesse; it seems clear to me, even without Peirce’s 1902
testimony, that even in 1880 he considers this realm just a limiting case of a broader
domain which cannot be ignored; in fact, in another 1880 paper, we find a harbinger of the
thought which was to be made explicit with the development of notations for
quantification:
To express the proposition: "If
S then P," first write
A
for this proposition. But the proposition is that a
certain conceivable state of things is absent from the universe of possibility. Hence
instead of A we write
B B
5
Then B expresses the possibility of S
being true and P false. Since, therefore, SS denies S, it follows
that (SS,P) expresses B. Hence we write
SS,P;SS,P
(CP 4.14).
This is close to the time of the "Illustrations
of the Logic of Science"; it might be argued that, with that series of essays
and with the significant contributions to symbolic logic dating from this period, we have
the beginnings of Peirce’s maturity as a philosopher-logician. And his theory of the
conditional—or, more generally, of the hypothetical—is consistent from
this point on, and is integral to his thought as a whole.
Examination of Peirce’s later work in logic strongly
supports this position. A decade after the Philosophy of Notation paper, Peirce had
changed notations. The algebraic notations we have been examining were successful vehicles
for his deductive logic; for a logic, however, it is not enough that a notation be
mathematically correct. The purpose of a logic is not efficient calculation. The purpose
is to provide an appropriate representation of the process of necessary deductive
reasoning; one of the measures of appropriateness, Peirce tells us, is iconicity (Zeman 1986, 13). And Peirce felt that his Existential Graphs were a more
appropriate representation of the subject matter of logic. The Graphs provide an
alternative and arguably more iconic (than the algebras) representation of a number of
features of deductive logic. The feature we are interested in at this point is the
relationship between the de inesse conditional and the "hypothetical."6
The most basic of the signs of the Existential Graphs is
the "Sheet of Assertion" (SA); SA is itself a graph, which represents whatever
is true about the universe of discourse; effectively, it represents that universe of
discourse. And
A proposition de inesse relates to
a certain single state of the universe, like the present instant. Such a proposition is
altogether true or altogether false. But it is a question whether it is not better to
suppose a general universe, and to allow an ordinary proposition to mean that is sometimes
or possibly true. Writing down a proposition under certain circumstances asserts it. Let
these circumstances be represented in our system of symbols by writing the proposition on
a certain sheet (CP 4.376).
It seems natural to employ a given SA to represent what
Peirce calls the "quasi-instantaneous" state of the general universe; Peirce
sometimes employs SA in this manner, and sometimes suggests other representations (or at
least that there are other representations; see ibid.; we shall eventually note at
least two specific cases in which Peirce sets separate "quasi-instantaneous"
states upon the same sheet). In 1903 Peirce tells us that
If a system of expression is to be adequate to the analysis of al necessary
consequences,7 it is requisite that it should be able to
express that an expressed consequent, C, follows necessarily from an expressed antecedent,
A. The conventions hitherto adopted do not enable us to express this. in order to form a
new and reasonable convention for this purpose we must get a perfectly distinct idea of
what it means to say that a consequent follows from an antecedent. It means that in adding
to an assertion of the antecedent an assertion of the consequent we shall be proceeding
upon a general principle whose application will never convert a true assertion into a
false one. . . . But before we can express any proposition referring to a
general principle, or as we say, to a "range of possibility," we must first find
means to express the simplest kind of conditional proposition, the conditional de
inesse, in which "If A is true, C is true means only that, principle or no
principle, the addition to an assertion of A of an assertion of C will not be the
conversion of a true assertion into a false one. That is, it asserts that the graph of Fig
1, anywhere on the sheet of assertion, might be transformed into the graph of Fig 2
without passing from truth to falsity.
 |
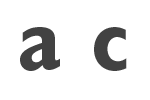 |
| Figure 1 |
Figure 2 |
This conditional de
inesse has to be expressed as a graph in such a way as distinctly
to express in our system both a and c and to exhibit their relation to one
another. To assert the graph thus expressing the conditional de inesse, it must be
drawn upon the sheet of assertion, and in this graph the expressions of a and c
must appear; and yet neither a nor c must be drawn upon the sheet of
assertion. How is this to be managed? (CP 4.435).
Peirce goes on to develop the typical alpha-graph
representation of the conditional. Significantly, he stresses iconicity:
In order to make the representation of the
relation between [antecedent and consequent] iconic, we must ask ourselves what spatial
relation is analogous to their relation (ibid).
His solution is the representation in Figure 3:
 |
| Figure 3 |
I have remarked that Peirce will give us ways of dealing
with more than one "quasi-instantaneous state" on a given sheet of assertion; he
also, however, describes sheets themselves as representing such states:
. . . in the gamma part of the
subject all the old kinds of signs take new forms. . . . Thus in place of a
sheet of assertion, we have a book of separate sheets, tacked together at points, if not
otherwise connected. For our alpha sheet, as a whole, represents simply a universe of
actual existent individuals, and the different parts of the sheet represent facts or true
assertions concerning that universe. At the cuts we pass into other areas, areas of
conceived propositions which are not realized. In these areas there may be cuts where we
pass into worlds which, in the imaginary worlds of the outer cuts, are themselves
represented to be imaginary and false, but which may, for all that, be true, and therefore
continuous with the sheet of assertion itself, although this is uncertain. You may regard
the ordinary blank sheet of assertion as a film upon which there is, as it were, an
undeveloped photograph of the facts in the universe. I do not mean a literal picture,
because its elements are propositions, and the meaning of a proposition is abstract and
altogether of a different nature from a picture. But I ask you to imagine all the true
propositions to have been formulated; and since facts blend into one another, it can only
be in a continuum that we can conceive this to be done. This continuum must clearly have
more dimensions than a surface or even than a solid; and we will suppose it to be plastic,
so that it can be deformed in all sorts of ways without the continuity and connection of
parts being ever ruptured. Of this continuum the blank sheet of assertion may be imagined
to be a photograph. When we find out that a proposition is true, we can place it wherever
we please on the sheet, because we can imagine the original continuum, which is plastic,
to be so deformed as to bring any number of propositions to any places on the sheet we may
choose (CP 4.512).
So the "alpha sheet . . . represents simply
a universe of actual existent individuals, and the different parts of the sheet represent
facts or true assertions concerning that universe." We seem to have "gates"8 into other universes: "At the cuts we pass into other
areas, areas of conceived propositions which are not realized."9
The model for the relationship between the universe of all possibles and the actual
universe is given geometrically (actually, topologically). Further, Peirce is not
interested only in "the" universe of actual existent fact, but as well in
certain other subsets of the realm of all possibles—he is interested in those subsets
which could themselves constitute existential universes.
. . . Now, qualities are
not, properly speaking, individuals. . . . Nevertheless, within limitations,
which include most ordinary purposes, qualities may be treated as individuals. At any
rate, however, they form an entirely different universe of existence. it is a universe of
logical possibility. As we have seen, although the universe of existential fact can only
be conceived as mapped upon a surface by each point of the surface representing a vast
expanse of fact, yet we can conceive the facts [as] sufficiently separated upon the map
for all our purposes; and in the same sense the entire universe of logical possibilities
might be conceived to be mapped upon a surface. Nevertheless, if we are going to represent
to our minds the relation between the universe of possibilities and the universe of actual
existent facts, if we are going to think of the latter as a surface, we must think of the
former as three-dimensional space in which any surface would represent all the facts that
might exist in one existential universe (CP 4.514).
So moving from the topological icon of the basic Sheet of
Assertion (considered to be a surface) as representing the universe of actual existent
fact, we take an appropriate space (that "surface" plus another dimension) as
representing the overall realm of possibles; other surfaces within that space would then
represent other possible existential universes. The "book of separate sheets, tacked
together at points, if not otherwise connected" of CP 4.512 is an approximation of
this "possibility space"; somehow the cuts (which are intimately associated with
the conditional) are means of passing from one possible existential universe to another.
It seems clear to me that the model here proposed for "the relation between the
universe of possibilities and the universe of actual existent facts" is also the
model for the relation between the hypothetical (which is concerned with the
universe of possibles in general) and the conditional de inesse (which focuses on
conditions at just one "quasi-instantaneous" state.
Peirce does not at this point see it possible to exploit
this model adequately:
In endeavoring to begin the construction
of the gamma part of the system of existential graphs, what I had to do was to select,
from the enormous mass of ideas thus suggested, a small number convenient to work with. It
did not seem to be convenient to use more than one actual sheet at one time; but it seemed
that various different kinds of cuts would be wanted (ibid.).
He suggests the "broken cut" as a way of
entering the broader universe of possibility; thus
 |
| Figure 4 |
does not assert that it
does not rain. it only asserts that the alpha and beta rules do not compel me to admit
that it rains, or what comes to the same thing, a person altogether ignorant, except that
he was well versed in logic so far as it [is] embodied in the alpha and beta parts of
existential graphs, would not know that it rained (CP 4.515).
He sketches out rules for this cut; our purpose at this
moment is not to explore these rules in detail except insofar as that exploration helps us
to investigate the model for the relationship of the possible to the realm of the de
inesse as Peirce tries to lay it out. The broken cut is a "possibly not"
operator, which Peirce uses in conjunction with the standard cut (simple negation) to
define the usual modal operators. Apropos of the aim of this paper, we note that he
employs this notation along with some different new signs:
CP 4.517 It must be remembered that
possibility and necessity are relative to the state of information.
 |
| Figure 5 |
Of a certain graph g
let us suppose that I am in such a state of information that it may be true and may
be false; that is I can scribe on the sheet of assertion Figs. 5 and 6.
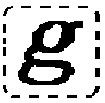 |
| Figure 6 |
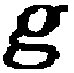 |
| Figure 7 |
 |
| Figure 8 |
Presumably, Fig 6 was "scribable" at one state
of our information, and ceased being so at a later state; Peirce will now suggest within
the graphs ways of representing such states (as we noted earlier, he had been talking
about such states and about quantification over them since the 1880's); some kind of
organized representation is needed, since
CP 4.518. You thus perceive that we should
fall into inextricable confusion in dealing with the broken cut if we did not attach to it
a sign to distinguish the particular state of information to which it refers. And a
similar sign has then to be attached to the simple g, which refers to the
state of information at the time of learning that graph to be true. I use for this purpose
cross marks below, thus:
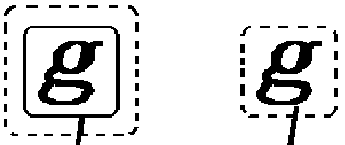 |
| Figure 9 |
These selectives are very peculiar in that they
refer to states of information as if they were individual objects. They have, besides, the
additional peculiarity of having a definite order of succession, and we have the rule that
from Fig. 10 we can infer Fig. 11.10
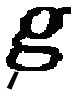 |
 |
| Figure 10 |
Figure 11 |
These signs are of great use in cleaning
up the confused doctrine of modal propositions as well as the subject of logical
breadth and depth.
Note that Peirce refers to the new "cross marks"
as selectives. This is a little unusual, since selectives are ordinarily letters of
the alphabet. It is clear, however, that he wishes these signs to be (implicitly)
quantified variables, which is precisely what selectives are. These selectives are in
appearance much like lines of identity, which is Peirce’s preferred form of
implicitly quantified variable in the graphs. I suggest that he thinks of them as
selectives because they show the "order of succession" he refers to, and show it
in a way that may not be quite as iconic as he would prefer; in the last two figures, the
order of succession is indicated by the single or the double nature of the crossmark
selectives. As we shall see, he also comes up with a representation of this situation
employing lines of identity. Before we examine that however, we take note of another
element that Peirce just mentions, the state of reflection:
There is not much utility in a double
broken cut. Yet it may be worth notice that Fig. 7 and
 |
| Figure 12 |
can neither of them be inferred from the other.
The outer of two broken cuts is not only relative to a state of information but to a state
of reflection. The graph asserts that it is possible that the truth of the graph g is
necessary (CP 4.519).
Peirce is here exploring a theory of modality, and his
exploration is continuous with the views on the conditional/hypothetical which had been
part of his approach to logic since about 1880, anyway. He had then written about states
of information (or of "things," or of "the speaker"), but had not had
a formal mathematical mechanism especially for such states—he had held that
they were capable of being represented in his quantified logic, as we have seen. With the
Gamma Graphs, he has a wealth of signs to help him deal with these "states"; as
he goes on:
CP 4.520. It becomes evident
. . . that a modal proposition is a simple assertion, not about the universe of
things, but about the universe of facts that one is in a state of information sufficient
to know. [Fig 6] without any selective, merely asserts that there is a possible state of
information in which the knower is not in a condition to know that the graph g
is true. We should naturally express this by Fig. 13.
 |
| Figure 13 |
But this is tosay that there
isaconceivable state of information in which the knower would know that g is
true. [This is expressed by] Fig. 10.
 |
| Figure 14 |
Now suppose we wish to assert that
there is a conceivable state of information in which the knower would know g
to be true and yet would not know another graph h to be true. We shall
naturally express this by Fig. 14.
Here we have a new kind of ligature, which
will follow all the rules of ligatures. We have here a most important addition to the
system of graphs. There will be some peculiar and interesting little rules, owing to the
fact that what one knows, one has the means of knowing what one knows—which is
sometimes incorrectly stated in the form that whatever one knows, one knows that one
knows, which is manifestly false (CP 4.521).
So Peirce applies ligatures—systems of lines of
identity—to the states of information. He makes suggestions that go even further,
introducing a sign specifically relating such states of information; this is effectively a
special "spot" whose 2 "hooks" are marked by the A and the B
below:
The truth is that it
is necessary to have a graph to signify that one state of information follows after
another. If we scribe
 |
| Figure 15 |
to express that the state of information B
follows after the state of information A, we shall have
 |
| Figure 16 |
This last is a version—employing lines of identity
("ligatures")—of the rule of necessitation done with "selectives"
in Fig. 10-11.
So we see that Peirce from about 1880 on, anyway, was
interested in what we recognize as "possible worlds" logic. He understood the
conditional as appropriately interpretable within such a context; he never really
"abandoned" the de inesse conditional, but through this entire period he
understood this "material implication" as a second to the larger third
of the "hypothetical," which cannot be understood outside this context of
possible states of information, states which can be "quantified over"; he
alludes to this quantification early on (in 1885, anyway). When he has, in the Existential
Graphs, what he considers an adequate notation for dealing with such matters, he discusses
and gives examples of such quantifications, as illustrated in the text and illustrations
we have been presenting. I note that in this material, Peirce is very close to our notion
of possible worlds semantics, and, indeed, may have something to teach us about it!
References
Fisch, Max.
1986, Peirce, Semeiotic, and Pragmatism,
Bloomington: Indiana.
Murphey, Murray G.
1961, The Development of Peirce's Philosophy,
Cambridge: Harvard.
Peirce, C. S.
1936-58, Collected Papers of C. S. Peirce,
v. 1-6 ed. Charles Hartshorne and Paul Weiss, v. 7-8 ed. Arthur Burks, Cambridge: Harvard.
1976, The New Elements of
Mathematics, v. 4, ed. Carolyn Eisele, The Hague: Mouton.
Prior, Arthur.
1955, "Diodorian Modalities," The
Philosophical Quarterly 5, 205-13.
1957, Time and Modality, London.
Robin, Richard S.
1967, Annotated Catalogue of the Papers of Charles
S. Peirce, Amherst: University of Massachusetts.
Zeman, J. Jay.
1973, Modal Logic: The
Lewis Modal Systems, Oxford: Clarendon Press.
1986, "Peirce's Philosophy
of Mathematics," Transactions of the Charles S. Peirce Society 22,
1-22.
Notes
*. Originally presented at the Peirce
Sesquicentential Conference at Harvard University, September 1989; published in Studies
in the Logic of Charles Sanders Peirce, Ed. Nathan Houser, Don D. Roberts,
& James Van Evra, Bloomington: Indiana University Press, 1997, 402-17.
1. Which term Peirce credits to none
other than:
Duns Scotus, who was a Philonian, [and who] as a matter of
course, threw considerable light upon the matter by distinguishing between an ordinary consequentia,
or conditional proposition, and a consequentia simplex de inesse. A consequentia
simplex de inesse relates to no range of possibilities at all, but merely to what
happens, or is true, hic et nunc. But the ordinary conditional proposition asserts
not merely that here and now either the antecedent is false or the consequent is true, but
that in each possible state of things throughout a certain well-understood range of
possibility either the antecedent is false or the consequent true. So understood the
proposition "If it lightens it will thunder" means that on each occasion which
could arise consistently with the regular course of nature, either it would not lighten or
thunder would shortly follow (NEM 4:169 [1898]).
2. The original discoverer was
Peirce (see Zeman 1986, 9); the other rediscoverer was, of course, Kripke.
3. Fisch at this point refers to CP 4.580
(1906) and CP 4.546 (1906, "Prolegomenon"). Although Peirce in
these passages does indeed advert to complications in the determination of the truth
values of conditionals, I find it difficult to interpret the passages’ actual text as
evidence of what we could call a "surrender of his last [nominalist]
stronghold," especially in the light of what I will argue about the early
Peirce’s view of the conditional. We might take as a summary of the arguments of
these paragraphs the conclusion of CP 4.580:
Some years ago [1903 is suggested by the Editors of CP]
when . . . I was led to revise [the] doctrine [that a mere possibility is an
absolute nullity], in which I had already found difficulties, I soon discovered, upon a
critical analysis, that it was absolutely necessary to insist upon and bring to the front,
the truth that a mere possibility may be quite real. That admitted, it can no longer be
granted that every conditional proposition whose antecedent does not happen to be realized
is true, and the whole reasoning just given breaks down.
4. The Editors of CP at
this point suggest looking at CP 3.527. This is an 1896 location which (especially in the
light of Peirce’s own 1908 comments on it) must be regarded as transitional to the
view of possibility developed by Peirce over the next decade in the Existential Graphs.
5. The propositional forms here are the
result of this being Peirce’s presentation of "A Boolian Algebra with one
constant," namely, "neither-nor."
6. We are about to examine some of
Peirce’s work in the logic of "Possible Worlds." At this point I will note
that his 1906 work in and about the Prolegomena to an Apology for Pragmaticism (CP
4.530 ff.) contains much potentially fruitful material in this direction, in the form of
his "Tinctured Existential Graphs." This is the topic of a paper in itself; it
takes somewhat different directions than those I am emphasizing here, and I will, in this
paper, just note the existence of the "Tinctures," and promise an investigation
of them at an early opportunity.
7. In the language of logic
"consequence" does not mean that which follows, which is called the consequent,
but means the fact that a consequent follows from an antecedent—csp.
8. As in contemporary science fiction!
9. This fits with his discussion of CP
4.435: "one should observe that the consequent of a conditional proposition asserts
what is true, not throughout the whole universe of possibilities considered, but in a
subordinate universe marked off by the antecedent. This is not a fanciful notion, but a
truth."
10. As the editors of CP
point out, this is effectively a rule of necessitation. It would appear that implicit in
this rule is that the first figure appears on the Sheet of Assertion by logical rule
rather than by contingency.