| Existential
Graphs - 4.372-417 |
| |
| |
Chapter
2: Symbolic Logic |
| |
CHAPTER
2 |
| |
SYMBOLIC
LOGIC(*1) |
| 372. |
If symbolic logic be defined as logic --
for the present only deductive
logic -- treated by means of a special system of
symbols, either devised for
the purpose or extended to logical from other uses, it
will be convenient not to
confine the symbols used to algebraic symbols, but to
include some graphical symbols
as well. |
| |
|
|
| 373. |
The first requisite to understanding this matter is to recognize
the purpose of a system of logical symbols. That purpose and end is simply and
solely the investigation of the theory of logic, and not at all the
construction of a calculus to aid the drawing of inferences. These two purposes
are incompatible, for the reason that the system devised for the investigation
of logic should be as analytical as possible, breaking up inferences into the
greatest possible number of steps, and exhibiting them under the most general
categories possible; while a calculus would aim, on the contrary, to reduce the
number of processes as much as possible, and to specialize the symbols so as to
adapt them to special kinds of inference. It should be recognized as a defect
of a system intended for logical study that it has two ways of expressing the
same fact, or any superfluity of symbols, although it would not be a serious
fault for a calculus to have two ways of expressing a fact. |
| |
|
|
| 374. |
There must be operations of transformation. In that way alone can
the symbol be shown determining its interpretant. In order that these
operations should be as analytically represented as possible, each elementary
operation should be either an insertion or an omission. Operations of
commutation, like xy .·.
yx, may be dispensed with by not recognizing any order
of arrangement as significant. Associative transformations, like (xy)z
.·. x(yz),
which is a species of commutation, will be dispensed with in the same way; that
is, by recognizing an equiparant(*1) as what it is, a symbol of an unordered
set. |
| |
|
|
| 375. |
It will be necessary to recognize two different operations,
because of the difference between the relation of a symbol to its object and to
its interpretant. Illative transformation (the only transformation, relating
solely to truth, that a system of symbols can undergo) is the passage from a
symbol to an interpretant, generally a partial interpretant. But it is
necessary that the interpretant shall be recognized without the actual
transformation. Otherwise the symbol is imperfect. There must, therefore, be a
sign to signify that an illative transformation would be possible. That is to
say, we must not only be able to express "A therefore B," but "If
A then B."
The symbol must, besides, separately indicate its object. This object must be
indicated by a sign, and the relation of this to the significant element of the
symbol is that both are signs of the same object. This is an equiparant, or
commutative relation. It is therefore necessary to have an operation combining
two symbols as referring to the same object. This, like the other operation,
must have its actual and its potential state. The former makes the symbol a
proposition "A is B;" that is, "Something A stands for,
B stands for." The
latter expresses that such a proposition might be expressed, "This stands for
something which A stands for and B stands for." These relations might be
expressed in roundabout ways; but two operations would always be necessary. In Jevons's modification(*1) of Boole's algebra the two operations are aggregation
and composition. Then, using non-relative terms, "nothing" is defined as that
term which aggregated with any term gives that term, while "what is" is that
term which compounded with any term gives that term. But here we are already
using a third operation; that is, we are using the relation of equivalence; and
this is a composite relation. And when we draw an inference, which we cannot
avoid, since it is the end and aim of logic, we use still another. It is true
that if our purpose were to make a calculus, the two operations, aggregation
and composition, would go admirably together. Symmetry in a calculus is a great
point, and always involves superfluity, as in homogeneous coördinates and in
quaternions. Superfluities which bring symmetry are immense economies in a
calculus. But for purposes of analysis they are great
evils. |
| |
|
|
| 376. |
A proposition de inesse relates to a single state of the universe,
like the present instant. Such a proposition is altogether true or altogether
false. But it is a question whether it is not better to suppose a general
universe, and to allow an ordinary proposition to mean that it is sometimes or
possibly true. Writing down a proposition under certain circumstances asserts
it. Let these circumstances be represented in our system of symbols by writing
the proposition on a certain sheet. If, then, we write two propositions on this
same sheet, we can hardly resist understanding that both are asserted. This,
then, will be the mode of representing that there is something which the one
and the other represent -- not necessarily the same quasi-instantaneous state
of the universe, but the same universe. If writing A asserts that A may be
true, and writing B that B may be true, then writing both together will assert
that A may be true and that B may be true. |
| |
|
|
| 377. |
By a rule of a system of symbols is meant a permission under
certain circumstances to make a certain transformation; and we are to recognize
no transformations as elementary except writing down and erasing. From the
conventions just adopted, it follows, as Rule 1, that anything written down may
be erased, provided the erasure does not visibly affect what else there may be
which is written along with it. |
| |
|
|
| 378. |
Let us suppose that two facts are so related that asserting the
one gives us the right to assert the other, because if the former is true, the
latter must be true. If A having been written, we can add B, we may then, by
our first rule, erase A; and consequently A may be transformed into
B by two
steps. We shall need to express the fact that writing A gives us a right, under
all circumstances, to add B. Since this is not a reciprocal relation, A and
B
must be written differently; and since neither is positively asserted, neither
must be written so that the other could be erased without affecting it. We need
some place on our sheet upon which we can write a proposition without asserting
it. The present writer's habit is to cut it off from the main sheet by
enclosing it within an oval line; but in order to facilitate the printing, we
will here enclose it in square brackets. In order, then, to express "If A can
under any circumstances whatever be true, B can under some circumstances be
true," we must certainly enclose A in square brackets. But what are we to do
with B? We are not to assert positively that B can be true; yet it is to be
more than hypothetically set forth, as A is. It must certainly, in some
fashion, be enclosed within the brackets; for were it detached from the
brackets, the brackets with their enclosed A could, by Rule 1, be erased; while
in fact the dependence upon A cannot be omitted without danger of falsity. It
is to be remarked that, in case we can assert that "If A can be true,
B can be
true," then, a fortiori, we can assert that "If both A and
C can be true, B can
be true," no matter what proposition C may be. Consequently, we have, as
Rule
2, that, within brackets already written, anything whatever can be inserted.
But the fact that "If A can be true, B can be true" does not generally justify
the assertion "If A can be true, both B and D are true"; yet our second rule
would imply that, unless the B were cut off, in some way, from the main field
within the brackets. We will therefore enclose B in parentheses, and express
the fact that "If A can be true, B can be true" by

The arrangement is without
significance. The fact that "If A can be true,
both B and D can be true," or [A(BD)], justifies the assertion that "If
A is true B
is true," or [A(B)]. Hence the permission of Rule 1 may be enlarged, and we may
assert that anything unenclosed or enclosed both in brackets and parentheses
can be erased if it is separate from everything else. Let us now ask what [A]
means. Rule 2 gives it a meaning; for by this rule [A] implies [A(X)], whatever
proposition X may be. That is to say, that [A] can be true implies that "If
A
can under any circumstances be true, then anything you like, X, may be true."
But we may like to make X express an absurdity. This, then, is a
reductio ad
absurdum of A; so that [A] implies, for one thing, that A cannot under any
circumstances be true. The question is, Does it express anything further?
According to this, [A (B)] expresses that A(B)
is impossible. But what is this?
It is that A can be true while something expressed by (B) can be true. Now,
what can it be that renders the fact that "If A can ever be true, B can
sometimes be true" incompatible with A's being able to be true? Evidently the
falsity of B under all circumstances. Thus, just as [A] implies that
A can
never be true, so (B) implies that B can never be true. But further, to say
that [A(B)], or "If A is ever true, B is sometimes true," is to say no more
than that it is impossible that A is ever true, B being never true. Hence, the
square brackets and the parentheses precisely deny what they enclose. A logical
principle can be deduced from this: namely, if [A] is true [A(X)] is true. That
is, if A is never true, then we have a right to assert that "If A is ever true,
X is sometimes true," no matter what proposition X may be. Square brackets and
parentheses, then, have the same meaning. Braces may be used for the same
purpose. |
| |
|
|
| 379. |
Moreover, since two negatives make an affirmative, we have, as
Rule 3, that anything can have double
enclosures added or taken away, provided there be
nothing within one enclosure but outside the other. Thus, if
B can be
true, so that B is written, Rule 3 permits us to write [(B)], and then Rule 2
permits us to write [X(B)]. That is, if B is sometimes true, then "If
X is ever
true, B is sometimes true." Let us make the apodosis of a conditional
proposition itself a conditional proposition. That is, in (C{D}) let us put for
D the proposition [A(B)]. We thus have (C{[A(B)]}). But, by Rule 3, this is the
same as (CA(B)). |
| |
|
|
| 380. |
All our transformations are analysed into insertions and
omissions. That is, if from A follows B, we can transform A into
A B and then
omit the B. Now, by Rule 1, from A B follows A. Treating this in the same way,
we first insert the conclusion and say that from A B follows A B A. We thus get
as Rule 4 that any detached portion of a proposition can be iterated. |
| |
|
|
| 381. |
It is now time to reform Rule 2 so as to state in general terms
the effect of enclosures upon permissions to transform. It is plain that if we
have written [A(B)]C, we can write [A(BC)]C, although the latter gives us no
right to the former. In place, then, of Rule 2 we have: Rule 2 (amended).
Whatever transformation can be performed on a whole
proposition can be performed upon any detached part of it under additional
enclosures even in number, and the reverse transformation can be performed
under additional enclosures odd in number.
But this rule does not permit every transformation which can be
performed on a detached part of a proposition to be performed upon the same
expression otherwise situated. |
| |
|
|
|
382. |
Rule 4 permits, by virtue of Rule 2
(amended), all iteration under additional enclosures and
erasure of a term inside enclosures if it is iterated
outside some of them. |
| |
|
|
| 383. |
We can now exhibit the modi tollens et ponens. Suppose, for
example, we have these premisses: "If A is ever true, B is sometimes true," and
"B is never true." Writing them, we have [A(B)](B). By Rule 4, from (B) we
might proceed to (B)(B). Hence, by Rule 2 (amended), from [A(B)](B) we can
proceed to [A](B), and by Rule 1 to [A]. That is, "A is never true." Suppose,
on the other hand, our premisses are [A(B)] and A. As before, we get [(B)]A,
and by Rule 3, B A, and by Rule 1, B. That is, from the premisses of the
modus ponens we get the conclusion. Let us take as premisses "If
A is ever true, B is
sometimes true," and "If B is ever true, C is sometimes true." That is,
(A{B})[B(C)]. Then iterating [B(C)] within two enclosures, we get
(A(B[B(C)]})[B(C)], or, by Rule 1, (A{B[B(C)]}). But we have just seen that
B[B(C)] can be transformed to C. Performing this under two enclosures, we get
(A{C}), which is the conclusion, "If A is ever true, C is sometimes true." Let
us now formally deduce the principle of contradiction [A(A)]. Start from any
premiss X. By Rule 3 we can insert [(X)], so that we have
X[(X)]. By insertion
under odd enclosures we have X[A(X)]. By iteration under additional enclosures
we get X[A(A X)]; by erasures under even enclosures [A(A)]. |
| |
|
|
| 384. |
In complicated cases the multitude of enclosures become
unmanageable. But by using ruled paper and drawing lines for the enclosures,
composed of vertical and horizontal lines, always writing what is more enclosed
lower than what is less enclosed, and what is evenly enclosed, on the left-hand
part of the sheet, and what is oddly enclosed, on the right-hand part, this
difficulty is greatly reduced. Fig. 65 |
| |
 |
|
Figure 65 |
|
| |
illustrates the general style of arrangement recommended. |
| |
|
|
| 385. |
It is now time to make an addition to our system of symbols.
Namely, A B signifies that A is at some quasi-instant true, and that
B is at
some quasi-instant true. But we wish to be able to assert that A and B are true
at the same quasi-instant. We should always study to make our representations iconoidal; and a very iconoidal
way of representing that there is one quasi-instant at
which both A and B are true will be to
connect them with a heavy line drawn in any shape, thus: |
| |
 |
| |
If this line be broken, thus
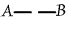 , the identity ceases to be asserted. We have
evidently: , the identity ceases to be asserted. We have
evidently:Rule 5. A line of identity may be broken where unenclosed.
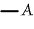 will mean
"At some quasi-instant A is true." It is equivalent to A simply. But will mean
"At some quasi-instant A is true." It is equivalent to A simply. But
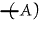 will
differ from will
differ from 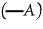 or
(A) in merely asserting that at some quasi-instant
A is not
true, instead of asserting, with the latter forms, that at no quasi-instant is
A true. Our quasi-instants may be individual things. In that case or
(A) in merely asserting that at some quasi-instant
A is not
true, instead of asserting, with the latter forms, that at no quasi-instant is
A true. Our quasi-instants may be individual things. In that case
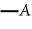 will mean
"Something is A"; will mean
"Something is A";
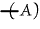 , "Something is not
A"; , "Something is not
A";
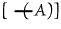 , "Everything is
A"; , "Everything is
A";
 , "Nothing is
A." So , "Nothing is
A." So
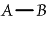 will express "Some
A is B"; will express "Some
A is B";
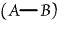 , "No
A is B"; , "No
A is B";
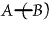 , "Some
A is not B"; , "Some
A is not B";
 , "Whatever
A there may be is B"; , "Whatever
A there may be is B";
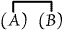 "There is something besides
A and B";(*1) "There is something besides
A and B";(*1)
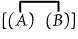 ,
"Everything is either A or B." ,
"Everything is either A or B." |
| |
|
| 386. |
The rule of iteration must now be amended as follows:
Rule 4 (amended). Anything can be iterated under the same enclosures or
under additional ones, its identical connections remaining identical.
Thus,
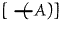 can be transformed to can be transformed to
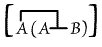 . By the same
rule . By the same
rule 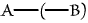 , i.e., "Something is
A and nothing is B," by iteration of the
line of identity, can be transformed to , i.e., "Something is
A and nothing is B," by iteration of the
line of identity, can be transformed to
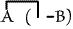 i.e., "Some
A is
not coexistent with anything that is B," whence, by Rules 5 and 2 (amended), it
can be further transformed to i.e., "Some
A is
not coexistent with anything that is B," whence, by Rules 5 and 2 (amended), it
can be further transformed to
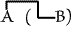 i.e., "Some
A is not B." i.e., "Some
A is not B." |
| |
|
|
| 387. |
But it must be most carefully observed that two unenclosed parts
cannot be illatively united by a line of identity. The enclosure of such a line
is that of its least enclosed part. We can now exhibit any ordinary syllogism.
Thus, the premisses of Baroko, "Any M is P" and "Some
S is not P," |
| |
 |
|
Figure 66 |
|
| |
may be written
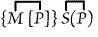 Then, as just seen, we can write Then, as just seen, we can write
 Then, by iteration, Then, by iteration,
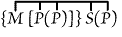 Breaking the line under
even enclosures, we get Breaking the line under
even enclosures, we get  But we have already shown that
[P(P)] can be written unenclosed. Hence it can be struck out under one
enclosure; and the unenclosed (P) can be erased. Thus we get But we have already shown that
[P(P)] can be written unenclosed. Hence it can be struck out under one
enclosure; and the unenclosed (P) can be erased. Thus we get
 or "Some
S is not M." The great number of steps into which syllogism is
thus analysed shows the perfection of the method for purposes of analysis. or "Some
S is not M." The great number of steps into which syllogism is
thus analysed shows the perfection of the method for purposes of analysis. |
| |
|
|
| 388. |
In taking account of relations, it is necessary to distinguish
between the different sides of the letters. Thus let
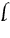 be taken in such a sense
that be taken in such a sense
that 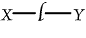 means "X loves
Y." Then means "X loves
Y." Then
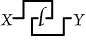 will mean "Y loves
X."
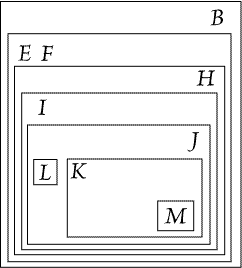
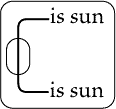
Then, if will mean "Y loves
X."
Then, if  means "Something is a man," and means "Something is a man," and
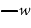 means "Something is a woman," means "Something is a woman,"
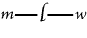 will mean "Some man loves some woman"; will mean "Some man loves some woman";
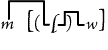 will mean
"Some man loves all women"; will mean
"Some man loves all women";
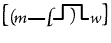 will mean "Every woman is
loved by some man," etc. will mean "Every woman is
loved by some man," etc. |
| |
|
|
| 389. |
Since enclosures signify negation, by enclosing a part of the line
of identity, the relation of otherness is represented. Thus,
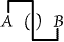 will assert "Some
A is not some B." Given the premisses "Some
A is B" and
"Some C is not B," they can be written will assert "Some
A is not some B." Given the premisses "Some
A is B" and
"Some C is not B," they can be written
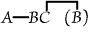 By Rule 3, this can
be written By Rule 3, this can
be written 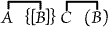 . By iteration, this gives . By iteration, this gives
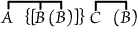 The lines of identity are to be conceived as passing through the space between
the braces outside of the brackets. By breaking the lines under even
enclosures, we get
The lines of identity are to be conceived as passing through the space between
the braces outside of the brackets. By breaking the lines under even
enclosures, we get 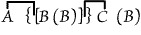 As we have already seen, oddly enclosed
[B(B)] can be erased. This, with erasure of the detached
(B), gives As we have already seen, oddly enclosed
[B(B)] can be erased. This, with erasure of the detached
(B), gives
 Joining the lines under odd enclosures, we get Joining the lines under odd enclosures, we get
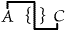 or
"Some A is not some C." or
"Some A is not some C." |
| |
|
|
| 390. |
For all considerable steps in ratiocination, the reasoner has to
treat qualities, or collections, (they only differ grammatically), and
especially relations, or systems, as objects of relation about which
propositions are asserted and inferences drawn. It is, therefore, necessary to
make a special study of the logical relatives " is a member of the collection
is a member of the collection ," and " ," and " is in the relation is in the relation
 to to
 ." The key to all that amounts to much in
symbolical logic lies in the symbolization of these relations. But we cannot
enter into this extensive subject in this article. ." The key to all that amounts to much in
symbolical logic lies in the symbolization of these relations. But we cannot
enter into this extensive subject in this article. |
| |
|
|
| 391. |
The system, of which the slightest possible sketch has been given,
is not so iconoidal as the so-called Euler's diagrams; but it is by far the
best general system which has yet been devised. The present writer has had it
under examination for five years with continually increasing satisfaction.
However, it is proper to notice some other systems that are now in use. Two
systems which are merely extensions of Boole's algebra of logic may be
mentioned. One of these is called by no more proper designation than the
"general algebra of logic."(*1) The other is called "Peirce's algebra of dyadic
relatives."(*2) In the former there are two operations -- aggregation, which Jevons
(*3) (to whom its use in algebra is due) signifies by a sign of division
turned on its side, thus 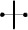 . (I prefer to join the two dots, in order to avoid
mistaking the single character for three); and composition, which is best
signified by a somewhat heavy dot, . (I prefer to join the two dots, in order to avoid
mistaking the single character for three); and composition, which is best
signified by a somewhat heavy dot,
 . .
Thus, if A and B are propositions,
A
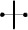 B is the proposition which is
true if A is true, is true if B is true, but is such that if A is false and B
is false, it is false. A
B is the proposition which is
true if A is true, is true if B is true, but is such that if A is false and B
is false, it is false. A
 B is the proposition which is true if A is true and B
is true, but is false if A is false and false if B is false. Considered from an
algebraical point of view, which is the point of view of this system, these
expressions A
B is the proposition which is true if A is true and B
is true, but is false if A is false and false if B is false. Considered from an
algebraical point of view, which is the point of view of this system, these
expressions A
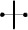 B and A
B and A
 B are mean functions; for a mean function is defined as
such a symmetrical function of several variables, that when the variables have
the same value, it takes that same value. It is, therefore, wrong to consider
them as addition and multiplication, unless it be that truth and falsity, the
two possible states of a proposition, are considered as logarithmic infinity
and zero. It is therefore well to let o represent a false proposition and
¥
(meaning logarithmic infinity, so that +
¥ and -
¥ are different) a true
proposition. A heavy line, called an "obelus," over an expression negatives it.
B are mean functions; for a mean function is defined as
such a symmetrical function of several variables, that when the variables have
the same value, it takes that same value. It is, therefore, wrong to consider
them as addition and multiplication, unless it be that truth and falsity, the
two possible states of a proposition, are considered as logarithmic infinity
and zero. It is therefore well to let o represent a false proposition and
¥
(meaning logarithmic infinity, so that +
¥ and -
¥ are different) a true
proposition. A heavy line, called an "obelus," over an expression negatives it.
The letters i, j, k, etc., written below the line after letters
signifying predicates, denote individuals, or supposed individuals, of which
the predicates are true. Thus, lij may mean that
i loves j. To the left of
the expression a series of letters
P and
S are written, each with a special one
of the individuals i, j, k attached to it in order to show in what order these
individuals are to be selected, and how.
Si will mean that
i is to be a
suitably chosen individual,
Pj that j is any individual, no matter what. Thus,
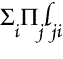
means that there is an individual i such that every individual
j loves i; and

will mean that taking any individual j, no matter what, there is some
individual i, whom j loves. This is the whole of this system, which has
considerable power. This use of S and
P was probably first introduced by O. C.
Mitchell in his epoch-making paper in Studies in Logic,(*4) by members of the
Johns Hopkins University. |
| |
|
|
| 392. |
In Peirce's algebra of dyadic relatives the signs of aggregation
and composition are used; but it is not usual to attach indices. In place of
them two relative operations are used. Let l be "lover of,"
s "servant of."
Then ls, called the relative product of s by l, denotes "lover of some servant
of"; and l*s, called the relative sum of l to
s, denotes "lover of whatever
there may be besides servants of." In ms. the tail of the cross will naturally
be curved. The sign | is used to mean "numerically identical with," and
 to
mean "other than." Schröder, who has written an admirable treatise on this
system (though his characters are very objectionable, and should not be used
(*1)), has considerably increased its power by various devices, and especially by
writing, for example, to
mean "other than." Schröder, who has written an admirable treatise on this
system (though his characters are very objectionable, and should not be used
(*1)), has considerably increased its power by various devices, and especially by
writing, for example, 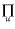 before an expression containing u to signify that
u
may be any relative whatever, or
before an expression containing u to signify that
u
may be any relative whatever, or
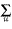 to signify that it is a possible relative.
In this way he introduces an abstraction or term of second intention. to signify that it is a possible relative.
In this way he introduces an abstraction or term of second intention. |
| |
|
|
| 393. |
Peano has made considerable use of a system of logical
symbolization of his own. Mrs. Ladd-Franklin(*1) advocates eight copula-signs to
begin with, in order to exhibit the equal claim to consideration of the eight
propositional forms. Of these she chooses "No a is b" and "Some a is
b"
(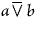 and and
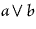 ) as most desirable for the elements of an algorithmic scheme;
they are both symmetrical and natural. She thinks that a symbolic logic which
takes "All a is b" (Boole, Schröder) as its basis is cumbrous; for every
statement of a theorem, there is a corresponding statement necessary in terms
of its contrapositive. This, she says, is the source of the parallel columns of
theorems in Schröder's Logik; a single set of theorems is all-sufficient if a
symmetrical pair of copulas is chosen. Some logicians (as C. S. P.) think the
objections to Mrs. Ladd-Franklin's system outweigh its advantages. Other
systems, as that of Wundt,(*2) show a complete misunderstanding of the problem. ) as most desirable for the elements of an algorithmic scheme;
they are both symmetrical and natural. She thinks that a symbolic logic which
takes "All a is b" (Boole, Schröder) as its basis is cumbrous; for every
statement of a theorem, there is a corresponding statement necessary in terms
of its contrapositive. This, she says, is the source of the parallel columns of
theorems in Schröder's Logik; a single set of theorems is all-sufficient if a
symmetrical pair of copulas is chosen. Some logicians (as C. S. P.) think the
objections to Mrs. Ladd-Franklin's system outweigh its advantages. Other
systems, as that of Wundt,(*2) show a complete misunderstanding of the problem. |
| |
|
|
| |
Chapter 3: Existential Graphs |
| |
CHAPTER 3 |
| |
EXISTENTIAL GRAPHS(*1) |
| |
A. THE CONVENTIONS |
| 394. |
Convention No. Zero. Any feature
of these diagrams that is not expressly or by previous
conventions of languages required by the conventions to
have a given character may be varied at will. This
"convention" is numbered zero, because it is understood
in all agreements. |
| |
|
|
| 395. |
Convention No. I. These Conventions are supposed to be mutual
understandings between two persons: a Graphist, who expresses propositions
according to the system of expression called that of Existential Graphs, and an
Interpreter, who interprets those propositions and accepts them without
dispute. A graph is the propositional expression in the System of Existential
Graphs of any possible state of the universe. It is a Symbol,(*1) and, as such,
general, and is accordingly to be distinguished from a graph-replica.(*P1) A
graph remains such though not actually asserted. An expression, according to
the conventions of this system, of an impossible state of things (conflicting
with what is taken for granted at the outset or has been asserted by the graphist) is not a graph, but is termed The
pseudograph, all such expressions
being equivalent in their absurdity. |
| |
|
|
| 396. |
It is agreed that a certain sheet, or blackboard, shall, under the
name of The Sheet of Assertion, be considered as representing the universe of
discourse, and as asserting whatever is taken for granted between the graphist
and the interpreter to be true of that universe. The sheet of assertion is,
therefore, a graph. Certain parts of the sheet, which may be severed from the
rest, will not be regarded as any part of it. |
| |
|
|
| 397. |
The graphist may place replicas of graphs upon the sheet of
assertion; but this act, called scribing a graph on the sheet of assertion,
shall be understood to constitute the assertion of the truth of the graph
scribed. (Since by 395 the conventions are only "supposed to be" agreed to, the
assertions are mere pretence in studying logic. Still they may be regarded as
actual assertions concerning a fictitious universe.) "Assertion" is not
defined; but it is supposed to be permitted to scribe some graphs and not
others. Corollary. Not only is the sheet itself a graph, but so likewise is the
sheet together with the graph scribed upon it. But if the sheet be blank, this
blank, whose existence consists in the absence of any scribed graph, is itself
a graph. |
| |
|
|
| 398. |
Convention No. II. A graph-replica on the sheet of assertion
having no scribed connection with any other graph-replica that may be scribed
on the sheet shall, as long as it is on the sheet of assertion in any way, make
the same assertion, regardless of what other replicas may be upon the sheet. The graph which consists of all the graphs on the sheet of assertion,
or which consists of all that are on any one area severed from the sheet, shall
be termed the entire graph of the sheet of assertion or of that area, as the
case may be. Any part of the entire graph which is itself a graph shall be
termed a partial graph of the sheet or of the area on which it is.
Corollaries. Two graphs scribed on the sheet are, both of them,
asserted, and any entire graph implies the truth of all its partial graphs.
Every blank part of the sheet is a partial graph. |
| |
|
|
| 399. |
Convention No. III. By a Cut shall be understood to mean a
self-returning linear separation (naturally represented by a fine-drawn or
peculiarly colored line) which severs all that it encloses from the sheet of
assertion on which it stands itself, or from any other area on which it stands
itself. The whole space within the cut (but not comprising the cut itself)
shall be termed the area of the cut. Though the area of the cut is no part of
the sheet of assertion, yet the cut together with its area and all that is on
it, conceived as so severed from the sheet, shall, under the name of the
enclosure of the cut, be considered as on the sheet of assertion or as on such
other area as the cut may stand upon. Two cuts cannot intersect one another,
but a cut may exist on any area whatever. Any graph which is unenclosed or is
enclosed within an even number of cuts shall be said to be evenly enclosed; and
any graph which is within an odd number of cuts shall be said to be oddly
enclosed. A cut is not a graph; but an enclosure is a graph. The sheet or other
area on which a cut stands shall be called the place of the cut. |
| |
|
|
| 400. |
A pair of cuts, one within the other but not within any other cut
that that other is not within, shall be called a scroll. The outer cut of the
pair shall be called the outloop, the inner cut the inloop, of the scroll. The
area of the inloop shall be termed the inner close of the scroll; the area of
the outloop, excluding the enclosure of the inloop (and not merely its area),
shall be termed the outer close of the scroll. |
| |
|
|
| 401. |
The enclosure of a scroll (that is, the enclosure of the outer cut
of the pair) shall be understood to be a graph having such a meaning that if it
were to stand on the sheet of assertion, it would assert de inesse that if the
entire graph in its outer close is true, then the entire graph in its inner
close is true. No graph can be scribed across a cut, in any way; although an
enclosure is a graph. (A conditional proposition de inesse considers only the existing state
of things, and is, therefore, false only in case the consequent is false while
the antecedent is true. If the antecedent is false, or if the consequent is
true, the conditional de inesse is true.) |
| |
|
|
| 402. |
The filling up of any entire area with whatever writing material
(ink, chalk, etc.) may be used shall be termed obliterating that area, and
shall be understood to be an expression of the pseudograph on that area. Corollary.
Since an obliterated area may be made indefinitely small, a
single cut will have the effect of denying the entire graph in its area. For to
say that if a given proposition is true, everything is true, is equivalent to
denying that proposition. |
| |
|
|
| |
§2. BETA PART |
| 403. |
Convention No. IV. The expression of a rheme in the system of
existential graphs, as simple, that is without any expression, according to
these conventions, of the analysis of its signification, and such as to occupy
a superficial portion of the sheet or of any area shall be termed a spot. The
word "spot" is to be used in the sense of a replica; and when it is desired to
speak of the symbol of which it is the replica, this shall be termed a
spot-graph. On the periphery of every spot, a certain place shall be
appropriated to each blank of the rheme; and such a place shall be called a
hook of the spot. No spot can be scribed except wholly in some area. |
| |
|
|
| 404. |
A heavy dot scribed at the hook of a spot shall be understood as
filling the corresponding blank of the rheme of the spot with an indefinite
sign of an individual, so that when there is a dot attached to every hook, the
result shall be a proposition which is particular in respect to every subject. |
| |
|
|
| 405. |
Convention No. V. Every heavily marked point, whether isolated,
the extremity of a heavy line, or at a furcation of a heavy line, shall denote
a single individual, without in itself indicating what individual it is. |
| |
|
|
| 406. |
A heavily marked line without any sort of interruption (though its
extremity may coincide with a point otherwise marked) shall, under the name of
a line of identity, be a graph, subject to all the conventions relating to
graphs, and asserting precisely the identity of the individuals denoted by its
extremities.
Corollaries. It follows that no line of identity can cross a cut.
Also, a point upon which three lines of identity abut
is a graph expressing the relation of teridentity. |
| |
|
|
| 407. |
A heavily marked point may be on a cut;
and such a point shall be interpreted as lying in the
place of the cut and at the same time as denoting an
individual identical with the individual denoted by the
extremity of a line of identity on the area of the cut
and abutting upon the marked point on the cut. Thus, in
Fig. 67, [Click here to view] [Click here to view], |
| |
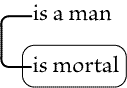 |
|
Figure 67 |
|
| |
if we refer to the individual
denoted by the point where the two lines meet on the
cut, as X, the assertion is, "Some individual, X,
of the universe is a man, and nothing is at once mortal
and identical with X"; i.e., some man is
not mortal. So in Fig. 68, |
| |
 |
|
Figure 68 |
|
| |
|
| |
if X and Y
are the individuals denoted by the points on the [inner]
cut, the interpretation is, "If X is the sun and
Y is the sun, X and Y are identical."
A collection composed of any line of identity together with all others
that are connected with it directly or through still others is termed a
ligature. Thus ligatures often cross cuts, and, in that case, are not graphs. |
| |
|
|
| 408. |
Convention No. VI. A symbol for a single individual, which
individual is more than once referred to, but is not identified as the object
of a proper name, shall be termed a Selective. The capital letters may be used
as selectives, and may be made to abut upon the hooks of spots. Any ligature
may be replaced by replicas of one selective placed at every hook and also in
the outermost area that it enters. In the interpretation, it is necessary to
refer to the outermost replica of each selective first, and generally to
proceed in the interpretation from the outside to the inside of all cuts. |
| |
|
|
| |
3. GAMMA PART |
| 409. |
Convention No. VII. The following spot-symbols shall be used, as
if they were ordinary spot-symbols, except for special rules applicable to
them: (Selectives are placed against the hooks in order to render the meanings
of the new spot-symbols clearer). |
| |
 |
| |
|
|
| 410. |
Convention No. VIII. A cut with many little interruptions(*1)
aggregating about half its length shall cause its enclosure to be a graph,
expressing that the entire graph on its area is logically contingent
(non-necessary). |
| |
|
|
| 411. |
Convention No. IX. By a rim shall be understood an oval line
making it, with its contents, the expression either of a rheme or a proper name
of an ens rationis. Such a rim may be drawn as a line of peculiar texture, or a
gummed label with a colored border may be attached to the sheet. A dotted rim
containing a graph, some part of which is itself enclosed by a similar inner
dotted oval and with heavy dotted lines proceeding from marked points of this
graph to hooks on the rim, shall be a spot expressing that the individuals
denoted by lines of identity attached to the hooks (or the single such
individual) have the character, constituted by the truth of the graph, to be
possessed by the individuals denoted by those points of it to which the heavy
dotted lines are attached, in so far as they are connected with the partial
graph within the inner oval. |
| |
|
|
| 412. |
A rim represented by a wavy line containing a graph, of which some
marked points are connected by wavy lines with hooks on the rim, shall be a
spot expressing that the individuals denoted by lines of identity abutting on
these hooks form a collection of sets, of which collection each set has its
members characterized in the manner in which those individuals must be which
are denoted by the points of attachment of the interior graph, when that graph
is true. |
| |
|
|
|
413. |
A rim shown as a saw line denotes an
individual collection of individual single objects or
sets of objects, the members of the collection being all
those in existence, which are such individuals as the
truth of the graph within makes those to be that are
denoted by points of attachment of that graph to saw
lines passing to hooks of the rim. |
| |
|
|
| |
B. RULES OF TRANSFORMATION |
| |
Pure Mathematical Definition of Existential Graphs,
Regardless of Their Interpretation |
| |
§1. ALPHA PART |
| 414. |
| 1. |
The System of Existential Graphs is a certain class of diagrams
upon which it is permitted to operate certain transformations.
|
| 2. |
There is required a certain surface upon which it is practicable to
scribe the diagrams and from which they can be erased in whole or in part.
|
| 3. |
The whole of this surface except certain parts which may be severed
from it by "cuts" is termed the sheet of assertion.
|
| 4. |
A graph is a legisign (i.e., a sign which is of the nature of a
general type) which is one of a certain class(z1) of signs used in this system. A
graph-replica is any individual instance of a graph. The sheet of assertion
itself is a graph-replica; and so is any part of it, being called the blank.
Other graph-replicas can be scribed on the sheet of assertion, and when this is
done the graphs of which those graph-replicas are instances is said to be
"scribed on the sheet of assertion"; and when a graph-replica is erased, the
graph is said to be erased. Two graphs scribed on the sheet of assertion
constitute one graph of which they are said to be partial graphs. All that is
at any time scribed on the sheet of assertion is called the entire scribed
graph.
|
| 5. |
A cut is a self-returning finely drawn line. A cut is not a
graph-replica. A cut drawn upon the sheet of assertion severs the surface it
encloses, called the area of the cut, from the sheet of assertion; so that the
area of a cut is no part of the sheet of assertion. A cut drawn upon the sheet
of assertion together with its area and whatever is scribed upon that area
constitutes a graph-replica scribed upon the sheet of assertion, and is called
the enclosure of the cut. Whatever graph might, if permitted, be scribed upon
the sheet of assertion might (if permitted) be scribed upon the area of any
cut. Two graphs scribed at once on such area constitute a graph, as they would
on the sheet of assertion. A cut can (if permitted) be drawn upon the area of
any cut, and will sever the surface which it encloses from the area of the cut,
while the enclosure of such inner cut will be a graph-replica scribed on the
area of the outer cut. The sheet of assertion is also an area. Any blank part
of any area is a graph-replica. Two cuts one of which has the enclosure of the
other on its area and has nothing else there constitute a double cut.
|
| 6. |
No graph or cut can be placed partly on one area and partly on
another.(*1)
|
| 7. |
No transformation of any graph-replica is permitted unless it is
justified by the following code of Permissions. |
|
|
| |
Code of Permissions |
|
415. |
|
Permission No.1 |
In each
special problem such graphs may be scribed
on the sheet of assertion as the conditions
of the special problem may warrant. |
|
Permission No.2 |
Any graph on
the sheet of assertion may be erased, except
an enclosure with its area entirely blank.
|
|
Permission No.3 |
Whatever
graph it is permitted to scribe on the sheet
of assertion, it is permitted to scribe on
any unoccupied part of the sheet of
assertion, regardless of what is already on
the sheet of assertion. |
|
Permission No.4 |
Any graph
which is scribed on the inner area of a
double cut on the sheet of assertion may be
scribed on the sheet of assertion. |
|
Permission No.5 |
A double cut
may be drawn on the sheet of assertion; and
any graph that is scribed on the sheet of
assertion may be scribed on the inner area
of any double cut on the sheet of assertion. |
|
Permission No.6 |
The reverse
of any transformation that would be
permissible on the sheet of assertion is
permissible on the area of any cut that is
upon the sheet of assertion. |
|
Permission No.7 |
Whenever we
are permitted to scribe any graph we like
upon the sheet of assertion, we are
authorized to declare that the conditions of
the special problem are absurd. |
|
| |
|
|
| |
§2. BETA PART |
| 416. |
| 8. |
The beta part adds to the alpha part certain signs to which new
permissions are attached, while retaining all the alpha signs with the
permissions attaching to them.
|
| 9. |
The line of identity is a Graph any replica of which, also called a
line of identity, is a heavy line with two ends and without other topical
singularity (such as a point of branching or a node), not in contact with any
other sign except at its extremities. Otherwise, its shape and length are
matters of indifference. All lines of identity are replicas of the same graph.
|
| 10. |
A spot is a graph any replica of which occupies a simple bounded
portion of a surface, which portion has qualities distinguishing it from the
replica of any other spot; and upon the boundary of the surface occupied by the
spot are certain points, called the hooks of the spot, to each of which, if
permitted, one extremity of one line of identity can be attached. Two lines of
identity cannot be attached to the same hook; nor can both ends of the same
line.
|
| 11. |
Any indefinitely small dot may be a spot replica called a
spot of
teridentity, and three lines of identity may be attached to such a spot. Two
lines of identity, one outside a cut and the other on the area of the same cut,
may have each an extremity at the same point on the cut. The totality of all
the lines of identity that join one another is termed a ligature.(z1)
A ligature is
not generally a graph, since it may be part in one area and part in another. It
is said to lie within any cut which it is wholly within.(z2) |
|
| |
|
|
| 417. |
| 12. |
The following are the additional permissions attaching to the
beta part. |
|
Code of Permissions -- Continued |
|
Permission No.8 |
All the
above permissions apply to all spots and to
the line of identity, as Graphs; and
Permission No. 2 is to be understood as
permitting the erasure of any portion of a
line of identity on the sheet of assertion,
so as to break it into two. Permission No. 3
is to be understood as permitting the
extension of a line of identity on the sheet
of assertion to any unoccupied part of the
sheet of assertion. Permission No. 3 must
not be understood [as stating that] that
because it is permitted to scribe a graph
without certain ligatures therefore it is
permissible to scribe it with them, or the
reverse. |
|
Permission No.9 |
It is permitted to
scribe an unattached line of identity on the
sheet of assertion, and to join such
unattached lines in any number by spots of
teridentity. This is to be understood as
permitting a line of identity, whether
within or without a cut, to be extended to
the cut, although such extremity is to be
understood to be on both sides of the cut.
But this does not permit a line of identity
within a cut that is on the sheet of
assertion to be retracted from the cut, in
case it extends to the cut. |
|
Permission No.10 |
If two spots
are within a cut (whether on its area or
not), and are not joined by any ligature
within that cut, then a ligature joining
them outside the cut is of no effect and may
be made or broken. But this does not apply
if the spots are joined by other hooks
within the cut.(*1)
|
|
Permission No.11 |
Permissions
Nos. 4 and 5 do not cease to apply because
of ligatures passing from without the outer
of two cuts to within the inner one, so long
as there is nothing else in the annular
area.(*2) |
|
| |
|
|
| |