![]()
Using
![]()
![]() offers a medium for working with Peirce’s Existential Graphs; it is an
application for Windows, written for the NET Framework 1.1. It currently has a
module which permits the construction of Alpha and Beta Existential Graphs
according to the “Rules of Illative Transformation” for Existential Graphs set
down and employed by Peirce from the 1890’s to 1909 or so. There also is a
module which permits the unrestricted generation of any “well-formed”
Existential Graphs; this is necessary both for experimentation and for the
generation of certain graphs which can be employed in the rule-bound version.
Eventually,
offers a medium for working with Peirce’s Existential Graphs; it is an
application for Windows, written for the NET Framework 1.1. It currently has a
module which permits the construction of Alpha and Beta Existential Graphs
according to the “Rules of Illative Transformation” for Existential Graphs set
down and employed by Peirce from the 1890’s to 1909 or so. There also is a
module which permits the unrestricted generation of any “well-formed”
Existential Graphs; this is necessary both for experimentation and for the
generation of certain graphs which can be employed in the rule-bound version.
Eventually,
![]() will be extended to parts of
Gamma as well, and we will add modules to deal explicitly with the semantics
of Existential Graphs (EG).
will be extended to parts of
Gamma as well, and we will add modules to deal explicitly with the semantics
of Existential Graphs (EG).
When
![]() is opened, what we see is
is opened, what we see is
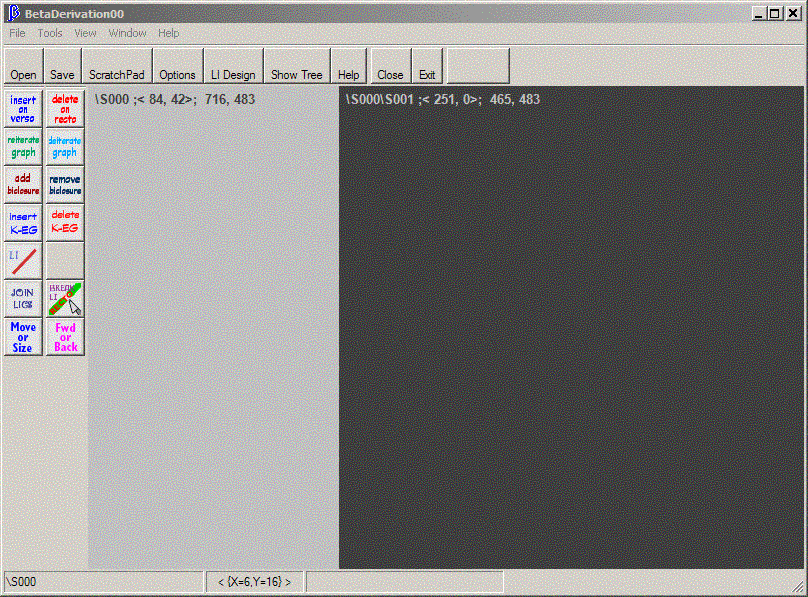 |
| Figure 1. BetaDerivations Form |
Clicking the "ScratchPad" Button or the "Tools > ScratchPad" Menu gives us
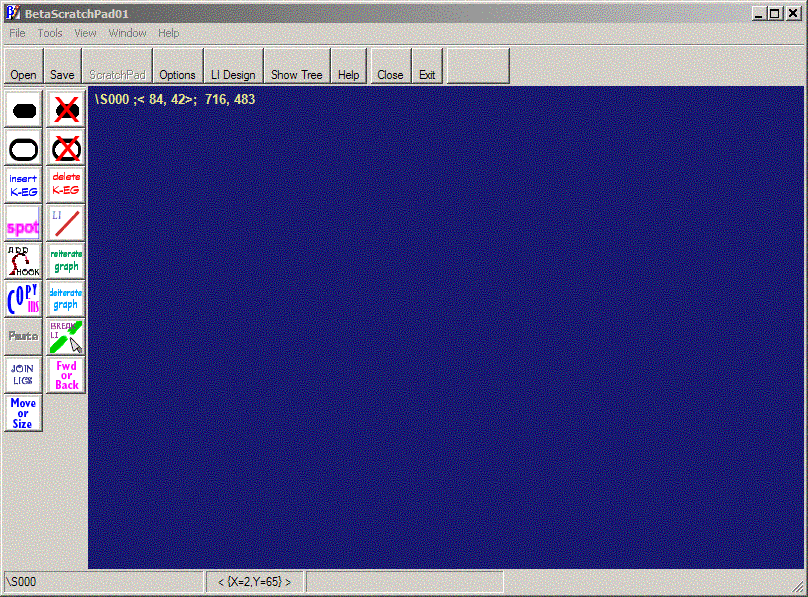 |
| Figure 2. Beta ScratchPad Form |
These are the basic media upon which Existential Graphs may be scribed and worked with. We will examine in some detail the basic Controls available to us for this work. First, though, we note that the main areas in the two Forms shown above are Sheets of Assertion for Existential Graphs. Actually, in the case of Figure 1, there are two Sheets of Assertion, or, perhaps, two sides of the same Sheet. The leftmost Sheet on that Form, named "S000"(n1) is, in fact a "Verso" area - meaning that it counts as "Oddly enclosed" in Peirce's rules of transformation for the Graphs; Sheet S001 is a "Recto"; it counts as "Evenly enclosed," and is what we normally think of as the Sheet of Assertion on which Graphs are constructed according to those rules of transformation. The Verso Sheet of Assertion in Figure 1 is an innovation which permits the "Insertion in Odd"(n2) of Hypotheses for the construction of a sort of "argument from hypotheses" on the Recto Sheet of Assertion (SA). The entire area in the Form of Figure 2 is a Recto Sheet of Assertion. The ScratchPad is used to construct any "well-formed" Beta Graph; this is useful for the experimentation which is an essential feature of this kind of logical work, and is essential for the creation of Graphs to be inserted on Verso areas of the BetaDerivations Form according with the rule we have just mentioned.
The Main Menus
The BetaDerivation and ScratchPad Forms share the Main Menu struture.
| The Menu Structure (click a link for description) | ||||||||||
|
| File > Open | Opens the "Open File" Dialog; permits
the opening of valid XML files as graph constructions; opens a new
instance of BetaDerivations in the proper format (Derivation or
ScratchPad) for the given file. Although a DTD for validating these
files is available at
http://www.existentialgraphs.com/dtd/BetaGraphs.dtd, the current
version of
|
||||||
| File > Save | Saves the graph construction of this instance, provided it has been named and saved; else, opens the "Save As" Dialog. | ||||||
| File > Save As | Opens the "Save As" Dialog; the graph construction may be saved as an XML file which may be opened as a graph construction, or as an SVG file, which may be viewed with an appropriate viewer or opened in certain graphics programs. | ||||||
| File > Save Screenshot |
|
||||||
| File > [recent file list] | As usual, permits the opening of recently used files. | ||||||
| File > Clear Recent Files | Clears the recent file list | ||||||
| File > Close Instance | Closes this instance of
|
||||||
| File > Exit | Closes
|
||||||
| Tools > ScratchPad | Opens a ScratchPad (see Figure 2), which permits the construction of any well-formed Beta Graph; such graphs may be inserted on Verso areas in the main construction. | ||||||
| Tools > Options |
|
||||||
| Tools > LIDesign |
|
||||||
| Tools > Show Tree |
|
||||||
| Tools > Set Root SA Size |
If the user requires precise control over the
physical size of the Construction, this Item affords it; clicking
this Menu Item gives the following Dialog:
Set the Width and Height and click "Set Size" |
||||||
| View > Line Connections |
|
||||||
| View >Diagnostic Labels | Diagnostic Labels are not displayed in the two graphs pictured above; they are, however, shown in previously pictured graphs. They consist of the path to the ContainerGraph, its location in pixels in form "<X, Y>", and its size in pixels in form "Width, Height." The Path shows the string of graphs in the Tree from the Root to the current graph. The Names of the graphs are of form "Snnn" for Sheets of Assertion, "Knnn" for ConjunctiveEGs, and "Cnnn" for Cuts. Diagnostic Labels are shown iff this item is checked. | ||||||
| View > Show Spot Borders |
|
||||||
| View > Hooks | Simply makes the Checked Menu Items for Hook Numbers and Hook Locations avaialble | ||||||
| View > Hooks > Hook Numbers | Hook Numbers (which are global within this construction) are displayed in the ParentGraph of the Hook's OwnerDot iff this item is checked. | ||||||
| View > Hooks > Hook Locations | Hook Locations are displayed as a contrasting round mark in the Hook's OwnerDot iff this item is checked | ||||||
| Window > Tile | Clicking this item causes Beta Derivation and ScratchPad Forms to be tiled on the available Desktop. Note that such forms may be open as new starts, or as the result of opening saved XML files. | ||||||
| Window > Cascade | Clicking this item Cascades the Forms. | ||||||
| Window > [open file list] | Transfers the focus to the Form whose entry is clicked. | ||||||
| Help > BetaDerivations Help | Gives access to Help. | ||||||
| Help > About BetaDerivations | Shows the "About BetaDerivations" screen. | ||||||
The Top ToolBar
This just offers convenience in doing some of the operations accessible through the Main Menus (click a Button for its function).
|
|
||||||||||||||||||
|
||||||||||||||||||
Context Menus
When you are constructing a Graph, any of the operations which may be performed at a given point on the surface of the Construction may be accessed by a right-click of the Mouse. The Context Menus which appear are the most basic way of doing these operations and are always available. They are not, however, the most convenient way of doing the construction, nor of learning how to do it. The available choices depend on whether we are working with a BetaDerivation or a ScratchPad, on the Type of Graph we are over and on its position in the Graph Construction; some other factors also enter here. The available Context Menu entries are a measure of what is permitted at a given point in a construction.
The Unrestricted Palette
We begin a discussion of constructing Graphs with the Palette of the ScratchPad, seen in Figure 2 above, and below left. Click a Button in the picture on the left for a discussion of that function (hovering the Mouse gives a brief tool-tip description).
|
|
|
The BetaDerivation Palette
We will continue with a discussion of the Palette used in the derivation of Beta Graphs according to the Rules of Transformation proposed by Peirce. This Palette is seen in Figure 1 above, as well as below to the left. As before, click a Button in the Palette as pictured below to go to a description of the function of that Button.
|
|
|