A Proof in for (x)(Ax É Bx) É ((x)Ax É (x)Bx)

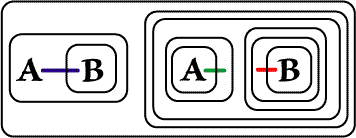
As usual, this proof begins with a Biclosure inserted on the Sheet of Assertion.

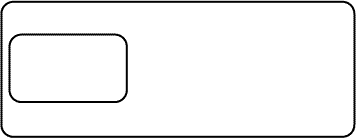Figure 1. Biclosure inserted on SA

We then insert a Graph equivalent to ($x)(Ax & ~Bx) in the Verso area of the Biclosure.

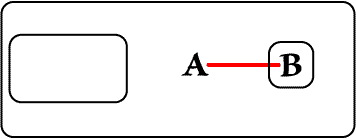Figure 2. Insertion on Verso

The next step is to Reiterate that Graph into the inner portion of the Biclosure; the Reiteration is done without maintaining a connection to the original Ligature, which results in a new Ligature (as you will notice, we are doing the version of the proof having turned off the facility to visibly connect separate Dots (Lines of Identity) of the same Ligature. Also, the Reiteration in is shown in two steps: the first is the insertion of a "ConjunctiveEG," which is a Container Graph which groups Graphs on the same area, and permits them to be acted upon (in this case Reiterated) as one. ConjunctiveEGs are implicit in the work of Peirce, who will often treat a set of Graphs in the same area as one Graph. The ConjunctiveEG is an equivalent of Conjunction in algebraic Logic; the Associativity/Commutativity of Conjunction permits ConjunctiveEGs to be made or removed at will. And with the Reiteration performed, they are removed in the last sub-step of Figure 3.

Figure 3. Reiteration

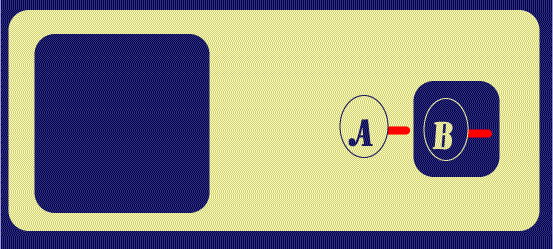
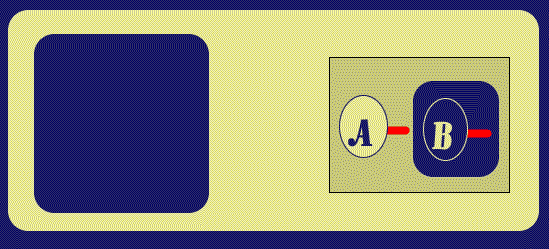
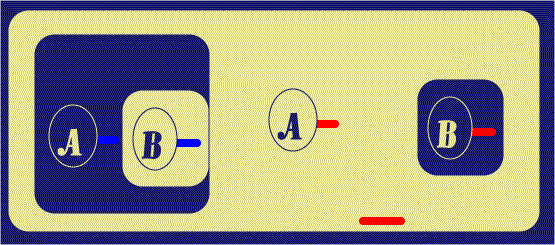
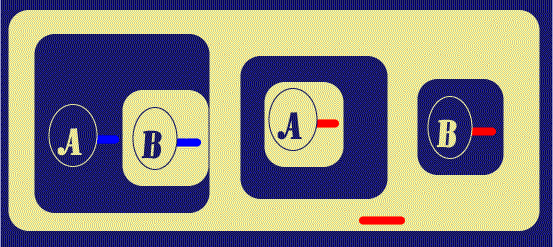
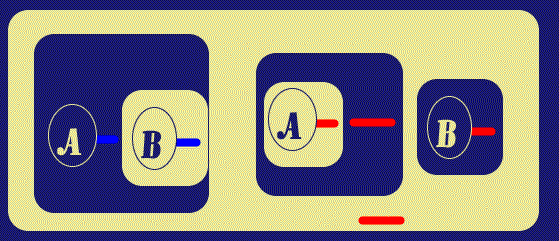
Next, a Biclosure is placed around the A-Spot in the Outer Close of the original Biclosure. Peirce states that Biclosures can be made or removed in Beta Graphs provided there is nothing in the annular space between them except for Ligatures passing all the way through; the gives us something of an analysis of this: first at Figure 4, I Reiterate the LI attached to the Hook of the A-Spot. The Copy is in the same Ligature as the Original, and stands in the same area (this is so that that Ligature can "maintain its presence" in that area). Then the Biclosure is inserted; in this way of doing it, we see that there is nothing at all in the annular space. Finally, the outer copy of Line of Identity is Reiterated into that annular space, with the new instance again being part of the same Ligature.

Figure 4. Insert another Biclosure

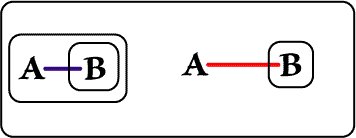
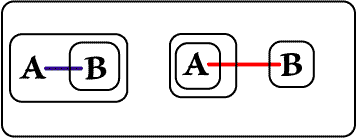
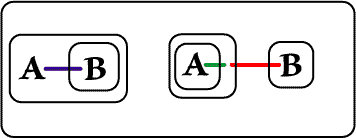
The just-reiterated LI is on the Recto part of the new Biclosure, and so, by Beta rules, may be broken. The break takes with it the LI attached to the Hook of the A-Spot, and we see a new Ligature.

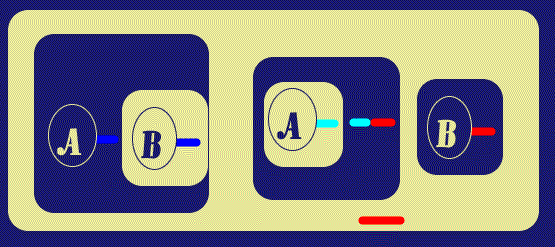Figure 5. Break Line of Identity on Recto

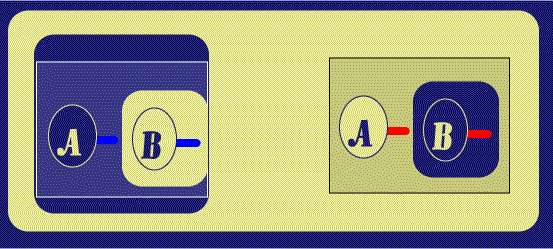
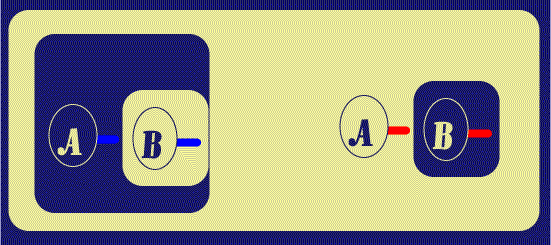
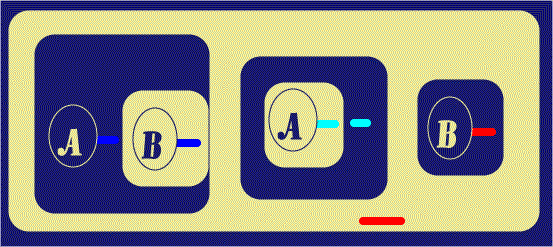
The next step is to withdraw the Red Ligature from this area, by Beta rules; in , this is done by Deiterating the Red Line of Identity Stub, leaving the other. The second sub-step of Figure 6 simply shows the outer Red Line of Identity moved to a convenient location for the next step.

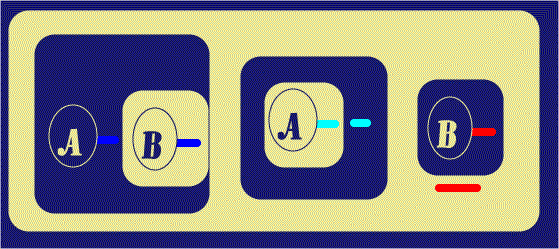Figure 6. Withdraw Line of Identity

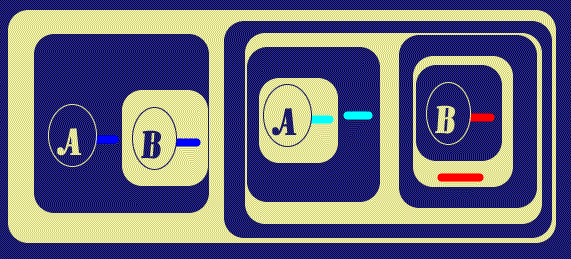
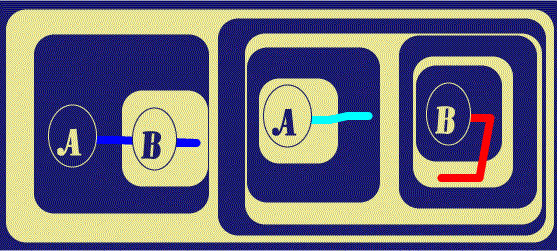
Next are two simple Alpha Biclosures which place the Graph into the form to be translated as

(x)(Ax É Bx) É ((x)Ax É (x)Bx)

Note that the Blue and Cyan Ligatures have their Scopes (GLBs in the Graph Tree) as  Recto Areas and the Red has a Verso Scope, making them Existential and Universal quantifications respectively (as indeed they are in the overall formula, as well as in the Graph). The final diagram shows the Ligatures with visible connections displayed over the Cuts in their sub-graphs.

Figure 7. Insert Two More Biclosures