| |
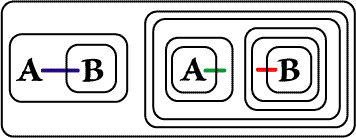
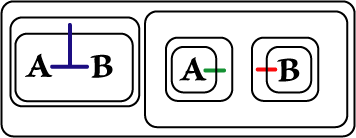
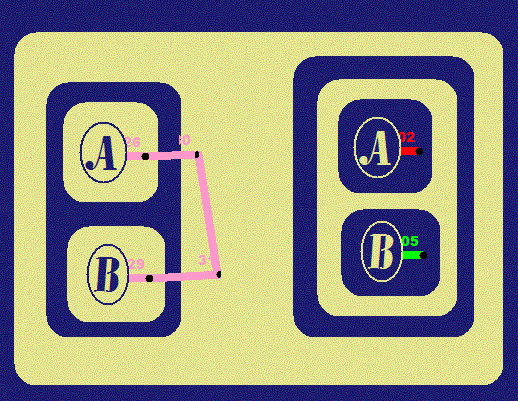
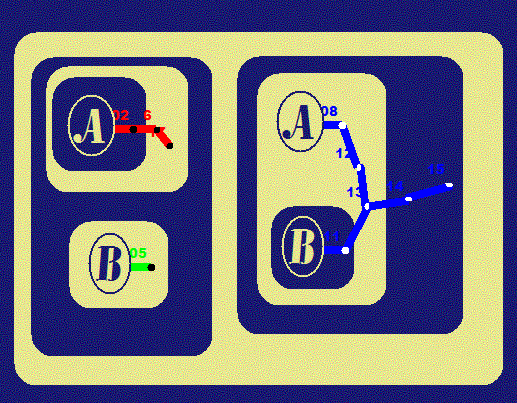
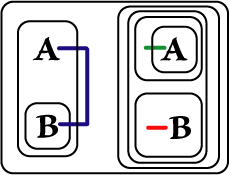
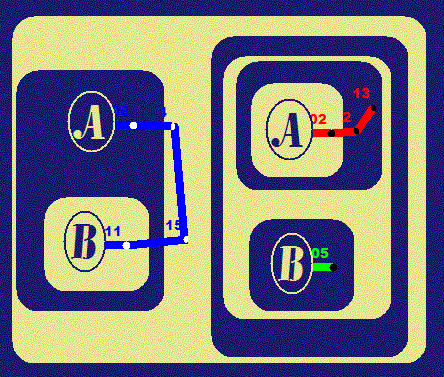
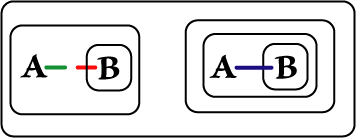
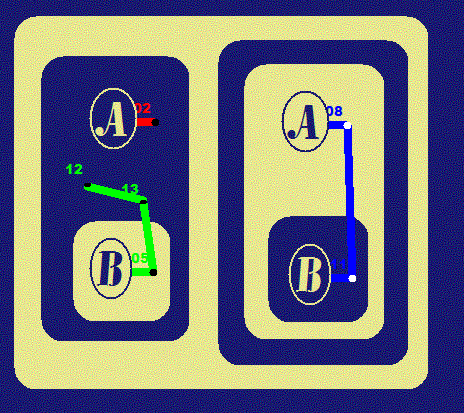
We will state these principles as implications and show
corresponding Beta Graphs. Diagrams on the left were prepared in
Adobe Illustrator; those on the right are done in
 . . |
| |
|
|
1 |
(x)(Ax
É
Bx)
É ((x)Ax
É
(x)Bx) |
|
|
|
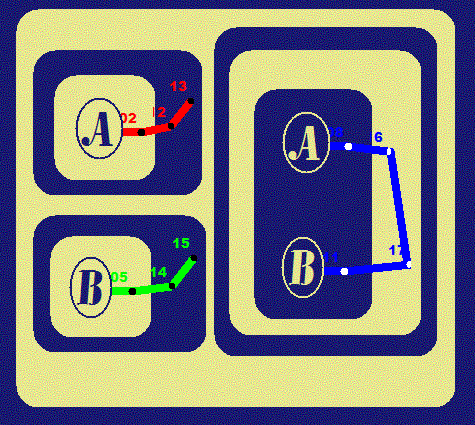
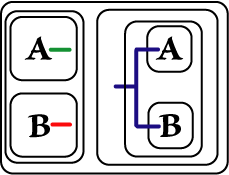
| 2 |
(x)(Ax
Ù
Bx)
É ((x)Ax
Ù
(x)Bx) |
|
|
|
| 3 |
((x)Ax
Ù
(x)Bx)
É (x)(Ax
Ù
Bx) |
|
|
|
| 4 |
(($x)Ax
Ú
($x)Bx)
É ($x)(Ax
Ú
Bx) |
|
|
|
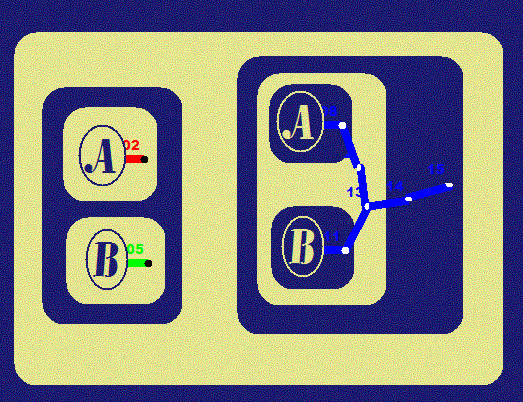
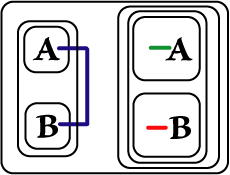
| 5 |
($x)(Ax
Ú
Bx)
É (($x)Ax
Ú
($x)Bx) |
|
|
|
| 6 |
((x)Ax
É
($x)Bx)
É ($x)(Ax
É
Bx) |
|
|
|
| 7 |
($x)(Ax
É
Bx)
É ((x)Ax
É
($x)Bx) |
|
|
|
| 8 |
(($x)Ax
É
(x)Bx)
É (x)(Ax
É
Bx) |
|
|
|
|
|
|
|
|
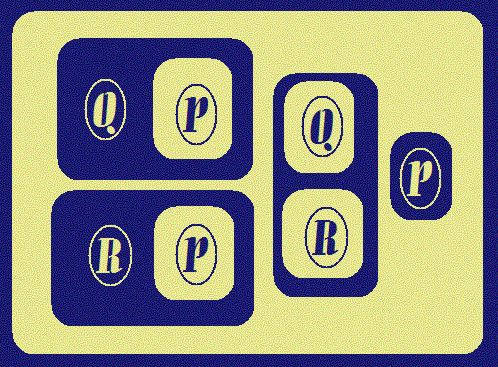
Some Useful Alpha-provable Graphs |
|
|
|
| 9 |
((P
É Q)
Ù (P
É R )
Ù P )
É
(Q
Ù R) |
| |
|
| 10 |
((Q
É P)
Ù (R
É P)
Ù
(Q
Ú R))
É P |
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|